【Python数据结构与算法实战】：构建高效数据处理系统的秘诀

# 1. Python数据结构基础

## 1.1 理解Python数据结构的重要性
Python是一门高级编程语言，以其简洁明了的语法而广受欢迎。掌握Python的基础数据结构，如列表（list）、元组（tuple）、字典（dict）和集合（set），是进行高效编程的基础。这些数据结构不仅在编写日常脚本中非常有用，而且对于处理复杂数据类型和算法开发至关重要。

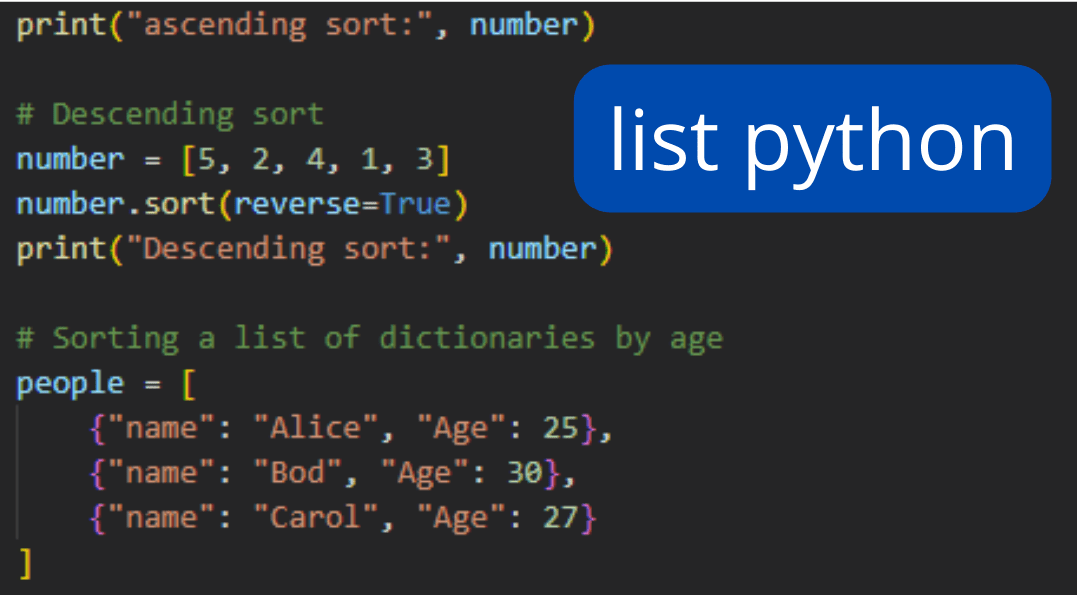
## 1.2 列表（List）
列表是Python中最常见的数据结构之一，本质上是一个可变的序列。它能够容纳不同类型的对象，并且支持增加、删除元素的操作，这使得列表在处理动态数据时十分灵活。例如：

my_list = [1, 2, 3]
my_list.append(4)

在上述代码中，我们创建了一个初始包含三个元素的列表，并使用`append`方法向其中添加了第四个元素。

## 1.3 字典（Dict）和集合（Set）
字典是一种映射类型，它存储键值对（key-value pairs），并允许我们快速检索与键相关联的值。这在需要存储和操作关联数据时非常有用。而集合是一个无序的、不重复的元素集，它主要用于进行成员资格测试和消除重复元素。

my_dict = {'key1': 'value1', 'key2': 'value2'}
my_set = set([1, 2, 3])

在以上代码片段中，我们创建了一个字典和一个集合。字典通过键来快速访问值，而集合则用于快速检查一个元素是否已存在于集合中。

随着我们深入探讨，我们会继续学习如何使用这些数据结构解决实际问题，同时分析它们的内部实现及其在Python中的性能特点。

# 2. 核心算法的实现与分析

## 2.1 常见算法类型概述

### 2.1.1 排序算法的原理与应用

排序算法是计算机程序设计中不可或缺的算法之一，用于将一系列数据按照一定的顺序排列。在众多的排序算法中，根据算法的时间复杂度、空间复杂度、稳定性和适用场景的不同，可以分为不同的类型。常见的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序和堆排序等。

以快速排序为例，该算法的基本原理是通过一个分治策略，将大的数组分成两个小数组去解决。快速排序的实现主要包括两部分：分区（Partition）和递归排序子序列。分区操作是将待排序的数组中的一个元素作为基准值（pivot），重新排列数组中的元素，使得所有元素小于等于基准值的都位于其左边，所有元素大于等于基准值的都位于其右边，此时基准值所在的索引位置即为整个数组的最终排序结果。

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

arr = [3, 6, 8, 10, 1, 2, 1]
print(quick_sort(arr))

快速排序的平均时间复杂度为O(nlogn)，在最好情况下也可以达到O(nlogn)，但最坏情况下的时间复杂度为O(n^2)，通常在随机数据中表现良好。由于其高效的性能，快速排序在实际应用中非常广泛，如数据库、文件系统和互联网搜索等。

### 2.1.2 搜索算法的效率对比

搜索算法用于在数据集合中查找特定元素的位置或值。基于数据结构的不同，搜索算法可以分为顺序搜索和二分搜索等类型。顺序搜索是指不考虑数据的任何特性，从头至尾遍历数据结构中的元素，直到找到目标值或遍历结束。而二分搜索则是一种在有序数组中查找特定元素的高效算法。

二分搜索首先将数组分为两半，判断目标值是在左半部分还是右半部分，然后根据比较结果继续在相应的半部分中进行搜索，直到找到目标值或确定目标值不存在为止。二分搜索的平均时间复杂度为O(logn)，是顺序搜索平均时间复杂度O(n)的优化版本，特别适用于大型数据集。

def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = left + (right - left) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

arr = [1, 3, 5, 7, 9, 11]
target = 7
print(binary_search(arr, target))

在性能要求较高的应用场景中，二分搜索通常是首选。尽管它的预处理要求数据必须有序，但它在搜索效率上远远超过了顺序搜索。不过，在数据频繁变动，且变动成本远大于一次完整的排序时，使用二分搜索的场景可能会受到限制。

## 2.2 高级数据结构探索

### 2.2.1 栈和队列的应用场景

栈（Stack）和队列（Queue）是两种常见的线性数据结构，它们在许多算法和实际应用中扮演着重要角色。栈是一种后进先出（LIFO, Last In First Out）的数据结构，它只允许在表的一端进行插入和删除操作。在算法问题中，栈可用于实现递归算法、表达式求值、括号匹配等问题的解决。

队列是一种先进先出（FIFO, First In First Out）的数据结构，它允许在表的一端进行插入操作，在另一端进行删除操作。队列常用于实现任务调度、缓冲处理、网络通信等场景。

class Stack:
    def __init__(self):
        self.items = []

    def push(self, item):
        self.items.append(item)

    def pop(self):
        return self.items.pop()

    def peek(self):
        return self.items[-1] if self.items else None

class Queue:
    def __init__(self):
        self.items = []

    def enqueue(self, item):
        self.items.append(item)

    def dequeue(self):
        return self.items.pop(0)

    def is_empty(self):
        return len(self.items) == 0

栈和队列的实现非常简单，但在合适的情景下使用它们，可以有效地解决复杂问题，例如深度优先搜索（DFS）和广度优先搜索（BFS）算法就可以通过栈和队列来实现。DFS利用栈的后进先出特性进行回溯，而BFS则用队列来按层次遍历图结构。

### 2.2.2 树与图的算法实现

树是一种层次数据结构，它由一个根节点和多个子树组成，每棵子树也是一个树结构。树在许多实际问题中都有应用，例如表示组织结构、表示文档的结构化信息、构建数据库索引等。树结构中比较重要的概念有二叉树、平衡树、B树和红黑树等。

图是一种复杂的非线性结构，由顶点（节点）和边组成，用于表示元素之间的复杂关系。图的算法实现需要处理图中的遍历（深度优先遍历、广度优先遍历）、路径搜索（如Dijkstra算法、Bellman-Ford算法、A*算法）、连通性问题（如Kruskal算法、Prim算法）等。