【Python数据处理中的图解】：图算法的应用详解

# 1. 图算法简介和应用场景

在计算机科学和数学领域，图算法是用来解决图论问题的一系列算法和技术。图是一种由顶点（节点）以及连接这些顶点的边组成的抽象数据结构，能够有效表达实体之间的复杂关系。图算法广泛应用于社交网络分析、网络优化、推荐系统、生物信息学等多个领域。

## 1.1 图算法在社交网络中的应用

在社交网络中，用户和用户之间的连接关系可以用图来表示，图算法可以帮助我们理解网络的结构特性，比如社区检测、影响力扩散和传播等。例如，通过识别社交网络中的关键节点（中心人物），我们可以对信息的传播路径和范围进行预测和控制。

## 1.2 图算法在推荐系统中的应用

推荐系统利用图算法来挖掘用户和物品之间的隐含关系，通过分析用户的历史行为数据生成个性化推荐。例如，基于图的协同过滤算法通过构建用户-物品的二部图，计算节点间的相似性，从而对用户可能感兴趣的商品进行推荐。

## 1.3 图算法在路网规划中的应用

在路网规划与分析中，地图可以被建模为一个加权有向图，其中节点代表路口，边代表路段，边的权重可以表示距离、行驶时间或者成本。图算法，特别是最短路径算法，比如迪杰斯特拉算法和弗洛伊德算法，在计算两点间的最优路径、交通流量预测和拥堵分析中发挥着重要作用。

在接下来的章节中，我们将深入探索图算法的基础理论，了解其复杂度分析，并且通过Python编程实现具体的图算法案例，进一步扩展和优化算法以适应各种实际问题。

# 2. 图算法的基础理论

## 2.1 图的基本概念

### 2.1.1 图的定义和表示方法

图是图算法中的基础数据结构，它由顶点（vertices）和边（edges）组成。顶点表示实体，边表示实体间的关系。图可以是有向的（边具有方向）或无向的（边没有方向）。

在数学和计算机科学中，图可以表示为G(V, E)，其中V代表顶点集合，E代表边集合。一个边可以表示为两个顶点的有序对(u, v)，其中u和v是V中的元素，并称作这条边的端点。

图的表示方法主要有以下几种：
- 邻接矩阵：使用二维数组表示图，适合于稀疏图。
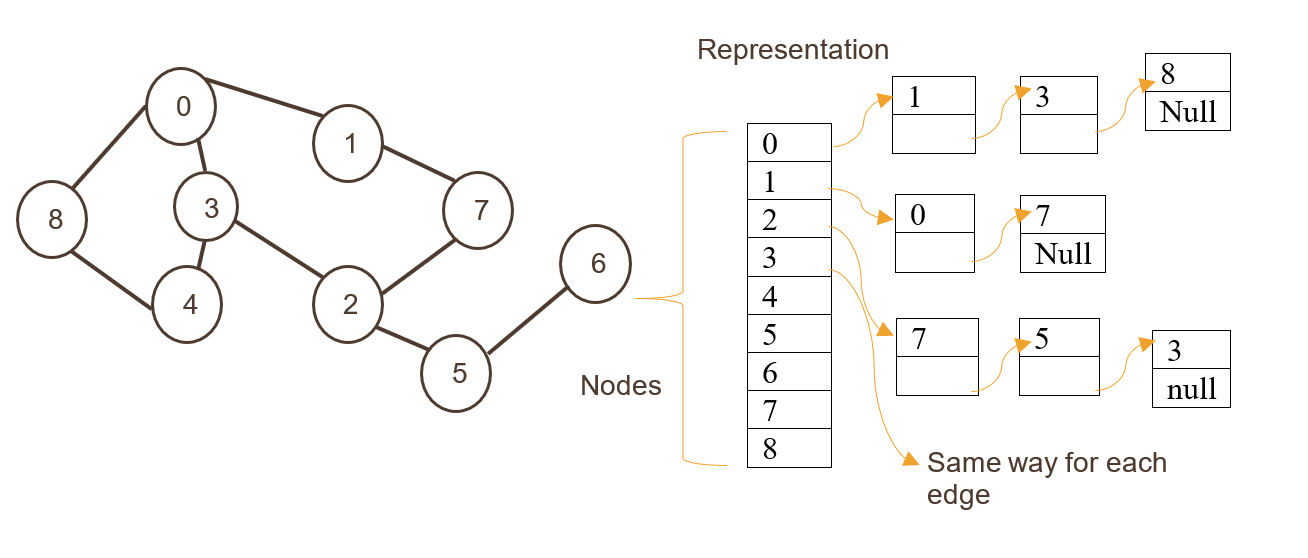
- 邻接表：使用链表或数组表示每个顶点的邻居，适合于稠密图。
- 边表：存储图的边信息，包括边的起点和终点。

**邻接矩阵示例代码：**

import numpy as np

# 创建一个4个顶点的空无向图
V = 4
G = np.zeros((V, V), dtype=int)

# 添加边 (0, 1), (0, 2), (1, 2), (2, 3)
G[0][1] = G[1][0] = 1
G[0][2] = G[2][0] = 1
G[1][2] = G[2][1] = 1
G[2][3] = G[3][2] = 1

print("Adjacency Matrix:")
print(G)

**邻接表示例代码：**

# 创建一个空图
graph = {i: [] for i in range(V)}

# 添加边 (0, 1), (0, 2), (1, 2), (2, 3)
graph[0].append(1)
graph[1].append(0)
graph[0].append(2)
graph[2].append(0)
graph[1].append(2)
graph[2].append(1)
graph[2].append(3)
graph[3].append(2)

print("Adjacency List:")
for key in graph:
    print(f"{key}: {graph[key]}")

### 2.1.2 图的遍历算法

图的遍历算法主要有深度优先搜索（DFS）和广度优先搜索（BFS）。

**深度优先搜索**：
- 概念：尽可能深地搜索图的分支。
- 方法：使用递归实现或栈实现。
- 用途：拓扑排序，解决迷宫问题等。

**广度优先搜索**：
- 概念：先访问离根节点最近的节点，然后访问离根节点次近的节点。
- 方法：使用队列实现。
- 用途：找到最短路径，拓扑排序等。

**DFS Python代码实现：**

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start, end=' ')
    for next in graph[start] - visited:
        dfs(graph, next, visited)
    return visited

visited = dfs(graph, 0)

**BFS Python代码实现：**

from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        vertex = queue.popleft()
        if vertex not in visited:
            print(vertex, end=' ')
            visited.add(vertex)
            queue.extend(graph[vertex] - visited)
    return visited

visited = bfs(graph, 0)

## 2.2 图算法的基本类型

### 2.2.1 最短路径算法

最短路径问题旨在找出加权图中两个顶点之间的最短路径。最常见的算法是Dijkstra算法和Floyd-Warshall算法。

**Dijkstra算法**：
- 算法步骤：
- 创建最短路径树集合S，最初包含起始顶点。
- 创建一个距离表，记录源点到每个顶点的最短路径长度估计值。
- 对于未访问的顶点，选择距离表中距离最小的顶点作为下一个访问的顶点。
- 更新未访问顶点的距离表值。
- 应用场景：GPS导航，网络中的路由算法等。

**Dijkstra算法Python实现：**

import sys

def dijkstra(graph, src):
    dist = {vertex: float('infinity') for vertex in graph}
    dist[src] = 0
    priority_queue = [(0, src)]

    while priority_queue:
        current_distance, current_vertex = priority_queue.pop(0)
        for neighbor, weight in graph[current_vertex].items():
            distance = current_distance + weight
            if distance < dist[neighbor]:
                dist[neighbor] = distance
                priority_queue.append((distance, neighbor))
    return dist

dijkstra_result = dijkstra(graph, 0)

### 2.2.2 最小生成树算法

最小生成树是加权无向图的一个子集，它是一个树结构，包含图中所有的顶点，并且边的总权重尽可能小。

**Kruskal算法**：
- 算法步骤：
- 将图中的所有边按照权重从小到大排序。
- 初始化一个最小生成树，开始时为空。
- 遍历排序后的边列表，将当前边加入最小生成树中，如果加入后没有形成环，则这条边被接受。
- 重复步骤3直到最小生成树中有V-1条边。
- 应用场景：网络设计，电路布线等。

**Kruskal算法Python实现：**

class DisjointSet:
    def __init__(self, vertices):
        self.parent = {}
        for vertex in vertices:
            self.parent[vertex] = vertex
    def find(self, item):
        if self.parent[item] != item:
            self.parent[item] = self.find(self.parent[item])
        return self.parent[item]
    def union(self, set1, set2):
        root1 = self.find(set1)
        root2 = self.find(set2)
        if root1 != root2:
            sel