特征工程实践案例：10个成功故事揭示特征构建的力量

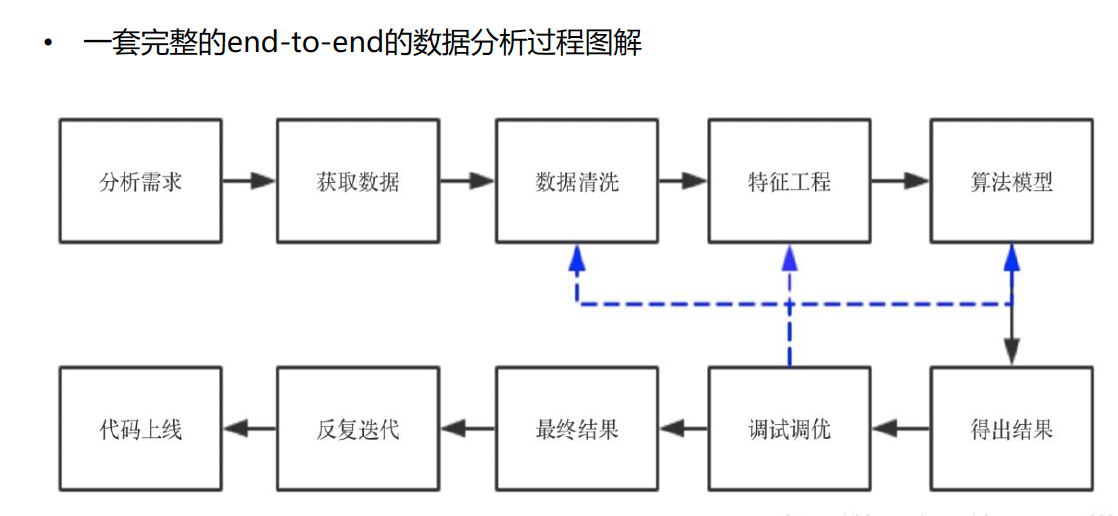
# 1. 特征工程在机器学习中的重要性

## 1.1 机器学习中的特征工程概述

在机器学习的工作流程中，特征工程是一个决定模型性能的关键步骤。特征工程的目的是从原始数据中提取有用的信息，以提高预测模型的准确性和效率。这一过程涉及对数据的理解、转换和优化，以便更好地满足算法的需求。

## 1.2 特征工程对模型的影响

高质量的特征可以显著提升模型的性能，而糟糕的特征可能会导致模型表现不佳。特征工程可以改善数据的表达方式，提高模型对关键信号的识别能力。例如，通过正确的特征组合，可以减少噪声的影响，增强信号的区分度，进而提升模型的泛化能力。

## 1.3 特征工程的实践意义

在实际应用中，特征工程往往需要反复的试验和调整。对特征的深入理解和创新的提取技巧，可以挖掘出数据中隐含的重要信息。此外，特征工程还可以帮助我们理解数据生成的过程和背后的原因，从而对业务决策提供更有价值的洞见。

通过下一章，我们将进一步探索数据预处理与特征提取的策略和方法，深入了解如何将原始数据转变为可供机器学习模型处理的高质量特征。

# 2. ```
# 第二章：数据预处理与特征提取技巧

## 2.1 数据清洗的策略和方法

数据清洗是特征工程中不可或缺的一步，它涉及到识别和修正数据集中存在的不一致性和错误。通过对数据的清洗，可以显著提升模型的性能和准确性。

### 2.1.1 缺失值的处理

缺失值是数据集中常见的问题，可能是由于数据录入错误、传输问题或其他因素造成。正确处理缺失值对于维持数据质量和模型性能至关重要。

- 删除含有缺失值的记录：简单但可能导致数据大量丢失。
- 填充缺失值：使用统计方法，如平均值、中位数或众数填充。
- 预测缺失值：利用机器学习模型，如随机森林或K最近邻算法。

**代码示例：**

import pandas as pd

# 假设df是包含缺失数据的DataFrame
df = pd.DataFrame({
    'A': [1, 2, np.nan, 4],
    'B': [5, np.nan, np.nan, 8],
    'C': [9, 10, 11, 12]
})

# 使用均值填充缺失值
df_filled = df.fillna(df.mean())

# 使用众数填充缺失值
df_mode_filled = df.fillna(df.mode().iloc[0])

在上述代码中，`fillna`函数用于填充缺失值。首先使用均值填充，然后使用众数填充。选择使用均值或众数取决于数据的分布和业务场景。

### 2.1.2 异常值的识别与处理

异常值是与数据集中其他数据点显著不同的观测值。它们可能是由于错误、变异或离群现象造成的。

- Z-Score方法：通过计算数据点与其均值的标准差倍数来识别异常值。
- IQR方法：基于四分位数范围来检测异常值。
- 基于模型的方法：使用聚类算法如K-means来识别离群点。

**代码示例：**

from scipy import stats

# 使用Z-Score识别异常值
z_scores = np.abs(stats.zscore(df[['A', 'B', 'C']]))
df['z_scores'] = z_scores.sum(axis=1)
df_outliers = df[df['z_scores'] > 3]  # 通常Z>3被认为是异常值

# 使用IQR识别异常值
Q1 = df[['A', 'B', 'C']].quantile(0.25)
Q3 = df[['A', 'B', 'C']].quantile(0.75)
IQR = Q3 - Q1
df_outliers_IQR = df[~((df[['A', 'B', 'C']] >= (Q1 - 1.5 * IQR)) & (df[['A', 'B', 'C']] <= (Q3 + 1.5 * IQR))).all(axis=1)]

在上述代码中，我们首先计算了每个数据点的Z-Score并识别出异常值，然后计算了四分位数范围并识别了异常值。异常值处理后，我们可以选择删除这些记录或对其进行适当的处理。

## 2.2 特征提取的核心技术

特征提取是从原始数据中提取有用信息的过程，以便模型可以更容易地发现数据中的模式和关系。

### 2.2.1 主成分分析(PCA)

PCA是一种常用的降维技术，它通过正交变换将一组可能相关的变量转换为一组线性不相关的变量，这些新变量称为主成分。

**代码示例：**

from sklearn.decomposition import PCA

# 假设X是数据矩阵
pca = PCA(n_components=2)  # 保留两个主成分
X_pca = pca.fit_transform(X)

# 查看解释的方差比率
print(pca.explained_variance_ratio_)

在上面的代码中，`PCA`函数用于将数据矩阵`X`转换为两个主成分。`explained_variance_ratio_`提供了每个主成分解释的方差量。

### 2.2.2 自编码器在特征提取中的应用

自编码器是一种无监督学习算法，通过训练网络压缩数据然后解压，可以学习到数据的有效表示。

**代码示例：**

from keras.layers import Input, Dense
from keras.models import Model

input_img = Input(shape=(input_dim,))
encoded = Dense(encoding_dim, activation='relu')(input_img)
decoded = Dense(input_dim, activation='sigmoid')(encoded)

autoencoder = Model(input_img, decoded)
***pile(optimizer='adam', loss='binary_crossentropy')

autoencoder.fit(X, X, epochs=50, batch_size=256, shuffle=True, validation_data=(X_test, X_test))

# 提取编码后的特征
encoded_imgs = encoder.predict(X)

在这个例子中，自编码器被训练来学习数据的有效表示，并将输入数据编码为较小的编码，然后再重构为原始数据。编码后的数据可以作为新的特征集合使用。

## 2.3 特征缩放和归一化

特征缩放和归一化是特征工程中的关键步骤，旨在消除不同特征间由于量纲差异带来的影响。

### 2.3.1 标准化与归一化的区别和应用

标准化（Standardization）将数据按属性（列）进行缩放，使其拥有均值为0和标准差为1的分布。

- 标准化适用于大多数机器学习算法，特别是对距离计算敏感的算法。
- 归一化（Normalization）将数据按比例缩放，将数据缩放到[0, 1]区间。

**代码示例：**

from sklearn.preprocessing import StandardScaler, MinMaxScaler

# 标准化
scaler_standard = StandardScaler()
X_standard = scaler_standard.fit_transform(X)

# 归一化
scaler_minmax = MinMaxScaler()
X_minmax = scaler_minmax.fit_transform(X)

在上述代码中，`StandardScaler`和`MinMaxScaler`分别用于标准化和归一化数据。根据不同的需求选择适当的方法是很重要的。

### 2.3.2 缩放技术的实际案例分析

在实际应用中，根据数据的分布和模型的需求选择合适的缩放方法至关重要。

- 使用标准化处理数据，当数据具有异常值时，可能需要进行异常值处理后再标准化。
- 归一化通常用于人工神经网络、k-最近邻和基于树的算法。

**案例分析代码示例：**

import numpy as np

# 模拟数据集，包含异常值
X = np.array([[1, 200], [2, 300], [3, 400]])
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 计算标准化后的均值和标准差
print("均值:", scaler.mean_)
print("标准差:", np.sqrt(scaler.var_))

在上面的例子中，我们首先创建了一个包含异常值的数据集，然后使用`StandardScaler`进行了标准化处理。通过查看处理后的均值和标准差，我们可以确认数据已被成功标准化。

# 3. 特征选择与优化方法

特征选择和优化是特征工程的关键环节，它们在减少模型复杂性、提高预测准确率以及增强模型泛化能力方面起着至关重要的作用。本章节将深入探讨特征选择的方法、实战案例以及优化策略。

## 3.1 常用特征选择技术

在特征选择过程中，算法需要区分哪些特征对模型的预测能力更为重要。常见方法包括过滤法、包裹法和嵌入法，它们各有特点和适用场景。

### 3.1.1 过滤法

过滤法是一种独立于模型的选择方法，它通过评估特征和目标变量之间的关系来选择特征。这一类方法通常依赖于统计测试，如卡方检验、ANOVA和相关系数。

from sklearn.feature_selection import SelectKBest, chi2

# 使用卡方检验进行特征选择
X_new = SelectKBest(chi2, k=10).fit_transform(X, y)

在这段代码中，我们使用了`SelectKBest`类和`chi2`方法从原始特征集合中选择出10个特征。`SelectKBest`类允许我们基于不同准则来选择特征，而`chi2`是专门用于分类问题的卡方检验，它可以帮助我们识别哪些特征与目标变量之间存在较强的相关性。

### 3.1.2 包裹法

包裹法涉及使用一个外部模型来评估特征组合的好坏。最著名的包裹法是递归特征消除（RFE）。

from sklearn.feature_selection import RFE
from sklearn.ensemble import RandomForestClassifier

# 使用RFE和随机森林进行特征选择
estimator = RandomForestClassifier(n_estimators=100)
selector = RFE(estimator, n_features_to_select=10, step=1)
X_new = selector.fit_transform(X, y)

上述代码中，我们使用了`RFE`类来包装随机森林分类器，通过逐步剔除特征的方式来选择最重要的10个特征。递归特征消除是一种强大的特征选择技术，因