CART决策树算法在机器学习中的权威指南

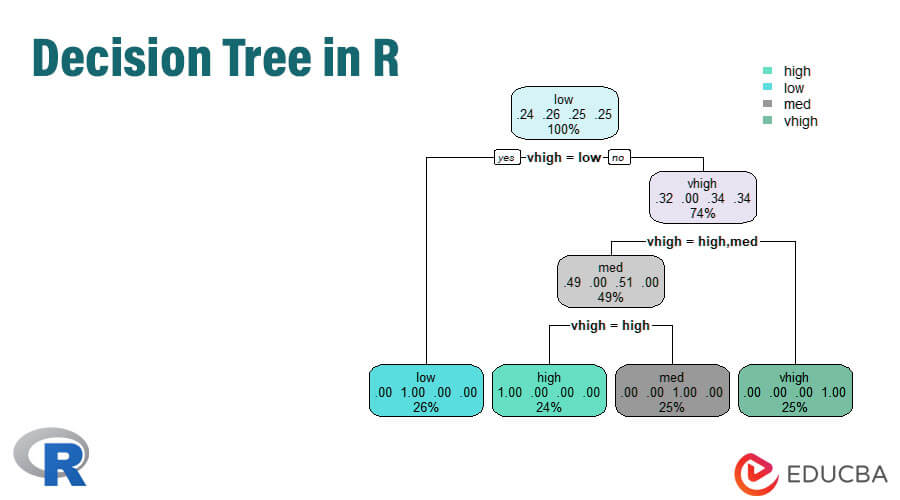
# 1. CART决策树算法概述**

CART（Classification And Regression Tree）决策树算法是一种广泛用于机器学习中的监督学习算法。它是一种非参数算法，可以处理分类和回归问题。CART决策树通过递归地将数据拆分成更小的子集来构建一个二叉树结构，其中每个节点代表一个特征，每个分支代表该特征的不同值。

CART决策树算法的关键思想是使用信息增益或基尼不纯度等度量标准来选择最佳的特征进行拆分。信息增益衡量特征将数据分成更纯净子集的程度，而基尼不纯度衡量数据集中不同类别的混合程度。算法将选择具有最高信息增益或最低基尼不纯度的特征作为拆分点，并继续递归地拆分数据，直到达到预定义的停止条件（例如，最大深度或最小样本数）。

# 2. CART决策树算法的理论基础

### 2.1 决策树的基本概念和算法

#### 2.1.1 决策树的结构和表示

决策树是一种树形结构，其中每个内部节点表示一个特征，每个分支表示该特征的可能取值，每个叶节点表示一个类标签或预测值。

        根节点
        /    \
       /      \
      /        \
     /          \
    /            \
   /              \
  /                \
 /                  \
/                    \
叶节点1            叶节点2

#### 2.1.2 决策树的构建算法

决策树的构建算法是一个递归过程，从根节点开始，根据以下步骤进行：

1. **选择特征：**选择一个最能区分不同类别的特征作为根节点。
2. **划分数据：**根据所选特征的取值将数据划分成子集。
3. **递归构建：**对每个子集重复步骤1和步骤2，直到所有数据都被划分到叶节点。

### 2.2 CART决策树算法的原理

CART（Classification and Regression Trees）决策树算法是一种二叉决策树，其构建过程基于以下两个准则：

#### 2.2.1 基尼不纯度和信息增益

**基尼不纯度**衡量数据集的异质性，计算公式为：

基尼不纯度 = 1 - Σ(p_i)^2

其中，p_i是数据集第i个类别的概率。

**信息增益**衡量一个特征划分数据集的有效性，计算公式为：

信息增益 = 基尼不纯度(父节点) - Σ(基尼不纯度(子节点) * 权重(子节点))

#### 2.2.2 CART决策树的构建过程

CART决策树的构建过程如下：

1. **选择特征：**选择具有最高信息增益的特征作为根节点。
2. **划分数据：**根据所选特征的取值将数据划分成子集。
3. **递归构建：**对每个子集重复步骤1和步骤2，直到所有数据都被划分到叶节点。
4. **叶节点的确定：**当一个子集中的所有数据都属于同一类别时，该子集成为叶节点。

# 3. CART决策树算法的实践应用

### 3.1 CART决策树算法在分类问题中的应用

#### 3.1.1 分类问题的建模和评估

**分类问题**是机器学习中常见的任务，其目标是将输入数据映射到一组预定义的类别。CART决策树算法可以有效地用于分类问题，其建模过程如下：

1. **数据准备：**收集和预处理数据，包括处理缺失值、异常值和特征缩放。
2. **决策树构建：**使用CART算法构建决策树，选择最佳分割属性和分割点，递归地将数据划分为更小的子集。
3. **模型评估：**使用交叉验证或留出法评估决策树的性能，计算准确率、召回率、F1分数等指标。

#### 3.1.2 CART决策树算法在分类问题中的实践

以下代码示例演示了如何使用CART决策树算法解决分类问题：

import pandas as pd
from sklearn.tree import