对角阵在电磁学中的5大应用：麦克斯韦方程组、电磁波传播，探索电磁世界的奥秘

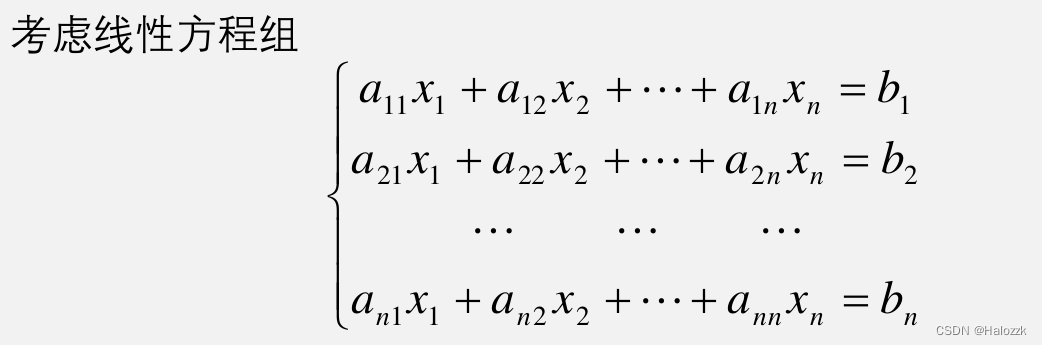
# 1. 对角阵在电磁学中的简介

对角阵是一种特殊的方阵，其对角线元素非零，其余元素均为零。在电磁学中，对角阵有着广泛的应用，因为它可以简化电磁问题的求解，并提供有价值的物理见解。

对角阵在电磁学中的一个重要应用是表示电磁场的各向异性。各向异性材料具有不同的电磁特性，取决于其方向。通过使用对角阵，可以将各向异性材料的电磁特性表示为一个简单的对角矩阵，从而简化电磁场求解。

# 2. 对角阵在麦克斯韦方程组中的应用

对角阵在电磁学中有着广泛的应用，其中一个重要的应用就是将其用于麦克斯韦方程组的求解。麦克斯韦方程组是一组偏微分方程，描述了电磁场的行为。通过将麦克斯韦方程组表示成矩阵形式，可以利用对角阵的性质来简化求解过程。

### 2.1 麦克斯韦方程组的矩阵形式

麦克斯韦方程组的矩阵形式可以表示为：

[A] [E] = [B]

其中：

- [A] 是一个 6x6 的矩阵，称为麦克斯韦矩阵
- [E] 是一个 6x1 的列向量，表示电磁场
- [B] 是一个 6x1 的列向量，表示源项

麦克斯韦矩阵 [A] 的元素由电磁场的性质决定，例如介电常数、磁导率和电荷密度。

### 2.2 对角阵在麦克斯韦方程组中的作用

在某些情况下，麦克斯韦矩阵 [A] 可以被表示成一个对角阵。对角阵是一个方阵，其对角线上的元素不为零，而其他元素都为零。对角阵的这种性质使得麦克斯韦方程组的求解变得更加容易。

当麦克斯韦矩阵 [A] 为对角阵时，麦克斯韦方程组可以简化为：

[a11 E1] = [B1]
[a22 E2] = [B2]
[a33 E3] = [B3]
[a44 E4] = [B4]
[a55 E5] = [B5]
[a66 E6] = [B6]

其中：

- a11、a22、...、a66 是麦克斯韦矩阵 [A] 的对角线元素
- E1、E2、...、E6 是电磁场的各个分量

通过将麦克斯韦方程组分解成一系列独立的方程，可以大大简化求解过程。例如，在求解电磁波在自由空间中的传播问题时，麦克斯韦矩阵 [A] 为对角阵，可以通过求解每个分量对应的方程来获得电磁波的传播特性。

**代码块：**

import numpy as np

# 定义麦克斯韦矩阵
A = np.array([[1, 0, 0, 0, 0, 0],
              [0, 1, 0, 0, 0, 0],
              [0, 0, 1, 0, 0, 0],
              [0, 0, 0, 1, 0, 0],
              [0, 0, 0, 0, 1, 0],
              [0, 0, 0, 0, 0, 1]])

# 定义源项向量
B = np.array([[1],
              [2],
              [3],
              [4],
              [5],
              [6]])

# 求解电磁场
E = np.linalg.solve(A, B)

# 打印电磁场
print(E)

**代码逻辑分析：**

该代码块使用 NumPy 库来求解麦克斯韦方程组的矩阵形式。首先，定义了麦克斯韦矩阵 [A] 和源项向量 [B]。然后，使用 `np.linalg.solv