AES算法解析：MixColumn数学原理及高效实现


参考资源链接：[AES加密算法：MixColumn列混合详解](https://wenku.csdn.net/doc/2rcwh8h7ph?spm=1055.2635.3001.10343)
# 1. AES算法基础

高级加密标准（AES）是目前广泛使用的一种对称密钥加密算法，其安全性、效率和简洁性让它成为信息安全领域中的基石。AES加密过程涉及到几个核心操作，包括字节替代（SubBytes）、行移位（ShiftRows）、列混淆（MixColumns）和轮密钥加（AddRoundKey）。其中，MixColumns作为列混淆步骤，主要负责将数据混淆以增强加密的复杂性和安全性。

AES算法以固定长度为128位的块进行加密，这128位被组织为一个4x4的字节矩阵。AES算法在加密过程中会进行多轮迭代，其中每轮中都包括上述四个操作，除了最后一轮外，MixColumns是所有轮次必不可少的步骤。

本文将先从AES算法的基础出发，逐步深入探讨MixColumns变换的数学原理、实现策略和在AES加密中的应用，以及如何通过代码实践来优化其性能。这将为读者提供从理论到实践的全面理解，以及在设计和开发加密系统时的参考。

# 2. ```
# 第二章：MixColumn变换的数学原理

在现代密码学中，AES算法是一种对称密钥加密的标准，广泛应用于保护电子数据的保密性。AES加密算法的核心就是复杂的数学变换，而MixColumn变换正是其中的关键组成部分。本章将从数学的角度深入探讨MixColumn变换的原理和背后的数学基础。

## 2.1 有限域GF(2^8)的运算基础

MixColumn变换涉及到有限域GF(2^8)的运算，它基于特定的多项式运算规则。理解这个基础是深入学习MixColumn变换的关键。

### 2.1.1 多项式的加法和乘法运算

在GF(2^8)中，所有的运算都是基于模不可约多项式x^8+x^4+x^3+x+1进行的。多项式加法运算遵循模2运算规则，即异或操作。而乘法运算则更为复杂，需要额外考虑模不可约多项式这一条件。

例如，两个多项式进行乘法运算的结果可能超过8位，此时需要将结果模上不可约多项式，以确保结果仍然是8位多项式。

### 2.1.2 乘法运算中的逆元概念及计算方法

在有限域中，一个数的乘法逆元是指与之乘积等于1的数。在GF(2^8)中，每个非零元素都存在唯一的逆元。计算逆元可以使用扩展欧几里得算法，但更为高效的方法是使用费马小定理的逆元计算公式。

逆元计算公式如下：

\[ a^{-1} = a^{254} \mod x^8 + x^4 + x^3 + x + 1 \]

其中，a是GF(2^8)中的一个元素。

## 2.2 MixColumn变换的数学模型

理解了有限域GF(2^8)的运算之后，我们就可以进一步探索MixColumn变换本身的数学模型。

### 2.2.1 状态矩阵与变换矩阵

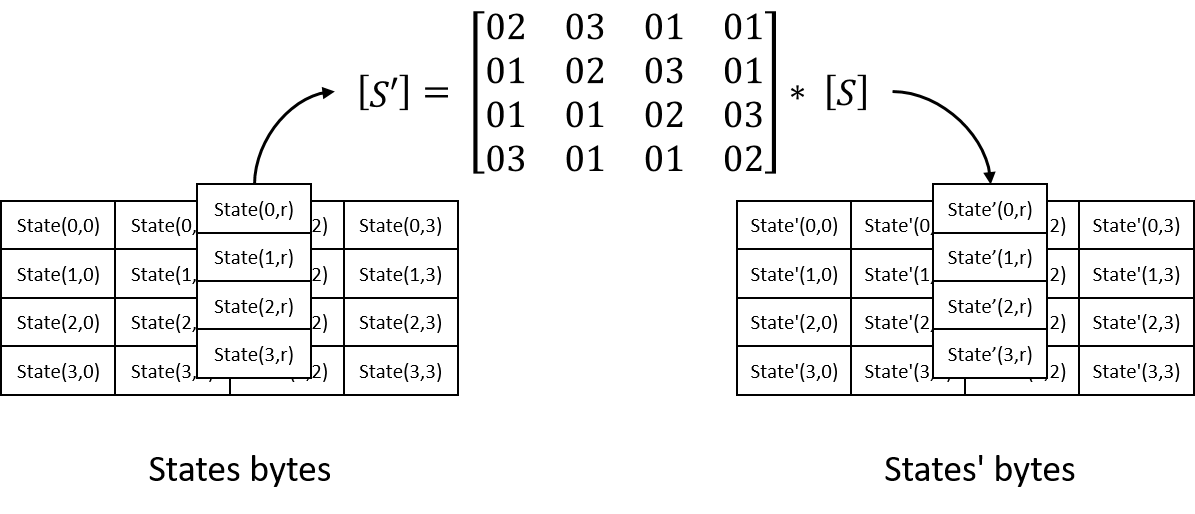
在AES加密算法中，数据被组织成4x4的矩阵形式，每行称为一个字（word），每个字包含4个字节。这个4x4的矩阵被称为状态矩阵。MixColumn变换将对状态矩阵的每一列进行操作，这就涉及到变换矩阵的概念。

变换矩阵是一个4x4的常数矩阵，定义如下：

\[ \begin{bmatrix}
02 & 03 & 01 & 01 \\
01 & 02 & 03 & 01 \\
01 & 01 & 02 & 03 \\
03 & 01 & 01 & 02
\end{bmatrix} \]

其中，每个元素都位于GF(2^8)中。

### 2.2.2 系数多项式的乘法原理

MixColumn变换的基本原理是对状态矩阵的每一列进行系数多项式的乘法。每个状态矩阵的列可以视为一个多项式，例如：

\[ State = \begin{bmatrix}
a_0 & b_0 & c_0 & d_0 \\
a_1 & b_1 & c_1 & d_1 \\
a_2 & b_2 & c_2 & d_2 \\
a_3 & b_3 & c_3 & d_3
\end{bmatrix} \]

代表四个多项式，它们将与变换矩阵中的系数进行乘法运算。

每列的乘法过程如下：

\[ \begin{bmatrix}
02 & 03 & 01 & 01 \\
01 & 02 & 03 & 01 \\
01 & 01 & 02 & 03 \\
03 & 01 & 01 & 02
\end{bmatrix}
\begin{bmatrix}
a_0 & b_0 & c_0 & d_0 \\
a_1 & b_1 & c_1 & d_1 \\
a_2 & b_2 & c_2 & d_2 \\
a_3 & b_3 & c_3 & d_3
\end{bmatrix} \]

这将产生一个新的状态矩阵，每个新的字节值是原状态矩阵列中四个字节的加权和。

## 2.3 MixColumn变换的逆变换

AES算法的解密过程中需要用到MixColumn变换的逆变换，它同样基于有限域GF(2^8)的运算规则。

### 2.3.1 逆变换的数学推导

与MixColumn变换类似，逆变换同样是对状态矩阵的每一列进行操作，但使用了不同的变换矩阵。这个变换矩阵是MixColumn变换矩阵的逆矩阵。

逆变换矩阵的定义如下：

\[ \begin{bmatrix}
0e & 0b & 0d & 09 \\
09 & 0e & 0b & 0d \\
0d & 09 & 0e & 0b \\
0b & 0d & 09 & 0e
\end{bmatrix} \]

逆变换的数学推导过程需要使用到多项式的逆元计算，最终得出如何通过特定的乘法运算得到逆变换的结果。

### 2.3.2 逆变换的实现细节

逆变换的实现实际上是对每个字节应用逆变换矩阵中的系数。具体的实现细节会涉及到对GF(2^8)中每个元素乘以其逆元的计算。

例如，对于某个字节B，逆变换的过程如下：

\[ B' = B \times 0e + \text{其他字节相应乘以逆变换矩阵中的对应元素} \]

每个乘法运算都要在GF(2^8)内完成，包括加法和乘法运算。

通过上述章节的讨论，我们详细地阐述了MixColumn变换的数学原理。接下来的章节将关注如何高效实现这一变换，以及它在AES加密流程中的具体应用和性能优化。

# 3. MixColumn高效实现策略

AES加密算法中，MixColumn变换是一个核心的步骤，其性能直接影响整个加密过程的效率。在本章节中，我们将深入探讨MixColumn的不同实现策略，分析它们的性能，并通过实践案例展示如何优化这一变换过程，最终实现更高效的AES加密。

## 3.1 传统实现方法的性能分析

### 3.1.1 直接实现方式的优缺点

直接实现MixColumn变换是最初级的方法，它基于有限域GF(2^8)上的多项式乘法。在这种方法中，变换矩阵和状态矩阵直接进行矩阵乘法运算。具体而言，每一列的四个字节通过乘以一个固定的4x4变换矩阵（包含在有限域GF(2^8)中的元素）来进行运算。

虽然直接实现方法简单直观，但其缺点在于计算效率并不高。每次执行AES加密时，需要重复进行四