探索AES加密：MixColumn变换的实用指南与优化策略


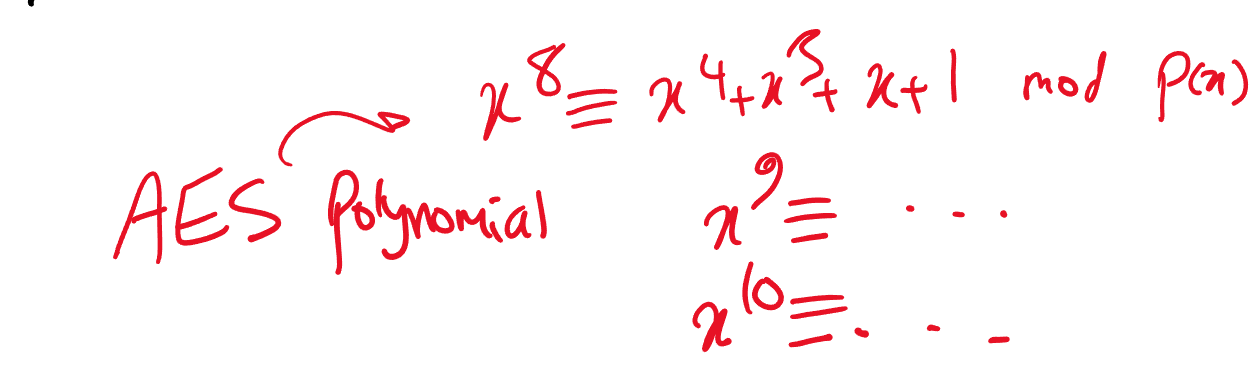
参考资源链接：[AES加密算法：MixColumn列混合详解](https://wenku.csdn.net/doc/2rcwh8h7ph?spm=1055.2635.3001.10343)
# 1. AES加密概述与MixColumn变换基础

## AES加密概述

高级加密标准（AES）是一种广泛应用于数据加密的对称加密算法。它被设计为能够抵御各种攻击，包括线性和差分密码分析。AES的加密过程涉及多个轮次的变换，其中包括初始轮、中间若干轮和最终轮。每一轮都包括四个基本步骤：字节替换（SubBytes）、行移位（ShiftRows）、列混淆（MixColumns）和轮密钥加（AddRoundKey）。其中，MixColumns变换是AES算法中实现混淆的关键步骤，它增强了加密过程的复杂性，从而提高安全性。

## MixColumn变换的作用

MixColumns变换在每一轮中对状态矩阵中的列进行操作。它将列视为多项式，并在有限域GF(2^8)上进行运算。这一变换的核心在于通过特定的矩阵乘法，实现列内元素的混合，使得任何一列的改变都会影响到该列的所有四个元素。这样一来，攻击者就很难通过分析单个字节的变化来推断密钥，从而显著提高了密码系统的安全性。

# 2. 深入理解MixColumn变换的数学原理

## 2.1 列混淆操作的矩阵解释

### 2.1.1 AES中的有限域 GF(2^8)

在密码学领域，特别是AES加密算法中，MixColumn变换利用了有限域GF(2^8)来执行多项式运算。有限域是由一组有限的元素构成的数学集合，它允许执行特定的加法和乘法规则。在GF(2^8)中，所有运算都是在模2^8的基础上进行的。这意味着，任何超出2^8范围的值都会被模2^8运算“截断”，只保留低8位。

在GF(2^8)中，多项式系数只能取0或1，这意味着所有的运算都可以通过位运算来实现，因此非常适合于计算机算法实现。AES算法中使用的生成多项式是x^8 + x^4 + x^3 + x + 1，即在GF(2^8)中多项式系数被限制在0和1之间。

### 2.1.2 MixColumn变换的矩阵乘法

MixColumn变换是一个混淆步骤，它作用于AES算法中的State（状态）的每一列上。State是一个由4行4列共16个字节组成的矩阵，每个字节都可以看作是GF(2^8)上的一个元素。MixColumn变换通过一个固定的4x4矩阵乘以State的每一列来实现。这个矩阵包含的是GF(2^8)中的系数，具体的变换公式如下：

| 02 | 03 | 01 | 01 |
| 01 | 02 | 03 | 01 |
| 01 | 01 | 02 | 03 |
| 03 | 01 | 01 | 02 |

在执行这个变换时，每一列都被视为一个多项式，然后与上述矩阵中的对应行做模x^4+1的多项式乘法。这一过程可以理解为一种特殊的矩阵乘法，其结果将得到新的列。

为了深入理解MixColumn变换的数学原理，我们需要深入了解在GF(2^8)上的多项式运算法则。下面的表格列出了GF(2^8)上的加法和乘法规则：

| 操作 | 描述 |
|:------:|:------:|
| 加法 | 对应位进行异或运算 (XOR) |
| 乘法 | 通过模x^8 + x^4 + x^3 + x + 1的乘法实现 |

这里不难发现，GF(2^8)上的加法实际上就是位运算中的异或操作，而乘法则稍微复杂，需要执行模多项式运算。

## 2.2 MixColumn变换的数学表示

### 2.2.1 多项式与矩阵乘法的关系

多项式运算是MixColumn变换的基础。在GF(2^8)中，每列可以表示为一个三次多项式，例如，如果列向量是(a3, a2, a1, a0)，则对应的多项式是a3x^3 + a2x^2 + a1x + a0。在进行MixColumn变换时，我们实际上是在将State的每个列多项式乘以变换矩阵中的对应行多项式。

这种运算的数学公式如下：

C(x) = {02, 03, 01, 01}[a3, a2, a1, a0]T

其中，C(x)表示列变换后的结果，[a3, a2, a1, a0]T表示原State列向量，而{02, 03, 01, 01}表示变换矩阵的一行。这个运算可以拆分为以下步骤：

1. 将每个系数乘以State列向量的对应元素。
2. 对结果执行GF(2^8)上的加法运算。

### 2.2.2 变换中使用的常数的数学性质

MixColumn变换中使用的常数具有特定的数学性质，这些性质在一定程度上决定了变换的安全性和效率。例如，02, 03, 01, 01这四个系数是经过精心选择的，它们保证了在GF(2^8)上的乘法运算具有良好的扩散效应和混淆性。

- 02，也称为α，在GF(2^8)上是一个元素的平方，因为它满足x^2 + 1 = 0。
- 03，即α + 1，在GF(2^8)上是一个既不是0也不是1的元素。
- 01，即1，它的作用是保持原有元素不变。

选择这些特定的系数能够保证在矩阵乘法中，State的每个字节都会影响到其他三个字节，从而使得即使攻击者获取了部分明文和密文，也难以推断出密钥信息。此外，这种设计也利用了有限域的数学性质，以确保变换的线性复杂度和良好的扩散性，增加了攻击破解的难度。

理解了MixColumn变换中的常数和它们的数学性质，我们可以更好地评估这些设计决策对于整个加密算法安全性的影响。这将为我们在实践中实现和优化AES加密提供坚实的理论基础。

# 3. MixColumn变换的实现与实践

MixColumn变换是高级加密标准（AES）中的一个关键步骤，负责数据的列混淆操作，极大提升了加密过程的复杂性，从而增强了加密算法的安全性。在本章节中，我们将探索MixColumn变换的软件和硬件实现方法，并对它们的性能进行分析。

## 3.1 MixColumn变换的软件实现

### 3.1.1 使用高级语言实现MixColumn

MixColumn变换可以通过高级编程语言如C/C++、Python等实现。在软件层面，我们通常关注算法的可读性、可维护性以及执行效率。

下面是一个使用C语言实现的MixColumn变换示例代码：

#include <stdint.h>

void mix_column(uint8_t *column) {
    uint8_t a[4], b[4];
    for (int i = 0; i < 4; i++) {
        a[i] = column[i];
        b[i] = column[(i + 1) % 4] ^ column[(i + 2) % 4] ^ column[(i + 3) % 4] ^ column[i];
    }

    column[0] = GF28_multiply(a[0], 2) ^ GF28_multiply(a[3], 3) ^ GF28_multiply(a[2], 1) ^ GF28_multiply(a[1], 1);
    column[1] = GF28_multiply(a[1], 2) ^ GF28_multiply(a[0], 3) ^ GF28_multiply(a[3], 1) ^ GF28_multiply(a[2], 1);
    column[2] = GF28_multiply(a[2], 2) ^ GF28_multiply(a[1], 3) ^ GF28_multiply(a[0], 1) ^ GF28_multiply(a[3], 1);
    column[3] = GF28_multiply(a[3], 2) ^ GF28_multiply(a[2], 3) ^ GF28_multiply(a[1], 1) ^ GF28_multiply(a[0], 1);
}

// 示例