密码学与AES加密：深入理解MixColumn变换的关键步骤与技巧


参考资源链接：[AES加密算法：MixColumn列混合详解](https://wenku.csdn.net/doc/2rcwh8h7ph?spm=1055.2635.3001.10343)
# 1. 密码学基础与AES概述

密码学是构建现代信息安全体系的基石，它涉及到信息的加密和解密，确保数据传输的机密性和完整性。在众多密码学算法中，高级加密标准（AES）因其高效性和可靠性成为了广泛使用的加密算法。AES不仅被美国政府采用，还被全球范围内众多企业和组织用于数据保护。本章将带您一起了解密码学的基础知识，并对AES进行概述，为深入探讨其内部工作机制打下基础。

## 密码学的基本概念

在密码学中，我们将明文（plaintext）转化为密文（ciphertext）的过程称为加密（encryption），其反向过程称为解密（decryption）。为了进行这些操作，我们需要使用密钥（key）和加密算法。密钥是一个秘密参数，用于控制加密和解密过程中信息的转换方式。而加密算法是一系列公式和规则，它们定义了如何使用密钥来操作数据。

## AES算法的由来与特点

高级加密标准（AES）是美国国家标准与技术研究院（NIST）在2001年提出的替代旧有的数据加密标准（DES）的算法。AES是分组密码算法，意味着它一次处理固定长度的数据块，而不是连续的数据流。AES的特点在于它的对称性，即同一个密钥可以用于加密和解密过程。AES的密钥长度可以是128位、192位或256位，提供不同的安全级别，但无论密钥长度如何，每个AES加密操作都是基于128位的数据块进行的。

## AES的加密流程概述

AES加密过程是一个迭代的、重复的算法流程，它主要由四部分组成：初始轮、若干中间轮和最终轮。每一轮都包含四个主要步骤：字节代换（SubBytes）、行移位（ShiftRows）、列混淆（MixColumns）和轮密钥加（AddRoundKey）。这些步骤反复执行，其中轮密钥加是利用轮密钥与数据块进行异或操作。最终轮会省略列混淆步骤，使得算法能够完成加密流程并输出最终的密文。

在下一章中，我们将深入探讨AES加密算法的核心组件，包括它的数学原理、密钥扩展算法以及MixColumns变换的理论基础。这将帮助我们更深入地理解AES的工作机制。

# 2. AES加密算法的核心组件

## 2.1 AES加密的数学原理

### 2.1.1 字节代换(BS)与有限域运算

在高级加密标准（AES）中，字节代换（Byte Substitution，BS）是一个基础操作，其目的是混淆数据，使得数据的统计特性变得不明显。字节代换过程基于一个固定的替换表，称为S盒（Substitution box）。每个字节输入至S盒，都会得到一个对应的输出，这个过程实际上是一个非线性的字节到字节的映射。

S盒的设计具有两个基本的特性：任意字节与S盒输出的差都不应为零，且与S盒输出差的逆不应为零。这样的设计能够确保特定的代数结构不会被轻易地透露出来，从而增加了密码学上的安全性。

有限域运算在AES中扮演了另一个关键角色。特别是在AES中的多项式算术操作中，定义在特定有限域上，这个域通常表示为GF(2^8)。在这个域中，基本的算术运算比如加法、乘法与模运算都与传统的算术不同。这种运算的特殊性为加密过程提供了额外的安全性。

### 2.1.2 行移位(RS)与列混淆(MC)

行移位（ShiftRows，SR）是AES中的另一个核心操作，它涉及到数据的行混合。在AES中，数据被组织为一个4x4的字节矩阵，即状态矩阵。行移位操作对这个矩阵的行进行移位操作，其中第一行不变，第二行循环左移一位，第三行循环左移两位，第四行循环左移三位。这样做的目的是为了使得数据的列之间产生复杂的依赖关系，从而增强加密的强度。

列混淆（MixColumns，MC）是另一个确保安全性的重要操作。该过程针对状态矩阵中的每一列，将它们视为多项式并进行乘以一个固定多项式的操作。结果是，每个列中的字节都会以一种复杂的方式相互影响，这大大增加了解密的难度。

## 2.2 AES中的密钥扩展算法

### 2.2.1 密钥生成过程详解

AES的密钥生成算法是整个加密过程的核心部分之一，它负责生成多个轮密钥，用于执行各个加密轮次。对于AES-128来说，初始密钥是128位长（即16字节），而整个密钥扩展过程可以生成11个128位的轮密钥，每一轮使用一个轮密钥。

密钥扩展过程可以分为以下几个步骤：

1. 将初始密钥复制到轮密钥数组中。
2. 对于每一个轮密钥（除了第一个轮密钥），密钥的最后一个字进行一个特定的变换，然后与前一个轮密钥的对应字进行异或操作。
3. 变换的输出会进入一个循环，其中包含一系列的替代和移位操作，最终生成新的轮密钥。

这种结构化的方法允许密钥在不同的轮次中以高度有序但又不完全相同的方式使用，从而提高了加密的复杂性和安全性。

### 2.2.2 密钥调度的数学基础

密钥调度的数学基础依赖于有限域上的算术运算。对于AES算法来说，使用了一个称为Rijndael多项式的特定构造，它基于GF(2^8)域上的元素。

每一步的密钥扩展操作都涉及到以下数学运算：

- 字节置换（SubByte）：这个操作和S盒替换一样，通过S盒得到新的字节。
- 循环移位（RotWord）：将一个字中的字节循环移动。
- 字节加（AddRoundKey）：对字节进行异或操作。
- 轮常数（Rcon）：在每次迭代中加入一个特定的轮常数。

这些操作的组合保证了轮密钥之间在数学上的强相关性，同时又使它们在结构上具有足够的差异性，这对于保证加密的安全性至关重要。

## 2.3 MixColumn变换的理论基础

### 2.3.1 矩阵与向量乘法在AES中的应用

在AES中，MixColumns变换是通过矩阵乘法来实现的。对于状态矩阵中的每一列，将其视为一个向量，并将其与一个固定的矩阵相乘。这个矩阵是4x4的，且其元素定义在有限域GF(2^8)中。

MixColumns变换中的矩阵如下所示：

3  1  1  1
1  3  1  1
1  1  3  1
1  1  1  3

每一个状态矩阵的列向量与该矩阵相乘时，实际上是在进行如下操作：

- 将每一列中的四个字节视为一个四次多项式。
- 将状态多项式乘以MixColumns矩阵中的多项式。
- 执行多项式乘法和模减法运算。

这样做的目的是实现所谓的"列混淆"，即对每一列的数据进行复杂的线性混合，以增强密码系统的安全性。

### 2.3.2 多项式运算及其与MixColumn的关系

AES中的多项式运算主要是在GF(2^8)域内完成的。这个域内的加法和乘法与传统的算术有本质的不同，因此需要特别的运算规则。

乘法规则采用了一个特殊的多项式作为模的生成元，即`x^8 + x^4 + x^3 + x + 1`。这个多项式是不可约的，意味着不能被分解为更小的多项式的乘积。在GF(2^8)域内进行乘法运算时，我们需要对乘积结果进行模这个生成元多项式的运算。

多项式运算与MixColumn变换的关系紧密，因为在执行列混淆操作时，我们实际上是在做多项式乘法。每一个状态矩阵的列，通过与固定矩阵的每一列相乘，实际上是在做多项式乘法运算。

例如，一个列向量`(b0,b1,b2,b3)`乘以MixColumns矩阵的第一列`(3,1,1,1)`实际上是计算如下多项式：

(b0*3 + b1 + b2 + b3) mod x^8 + x^4 + x^3 + x + 1

这个计算确保了列向量的四个字节被混合，且这种混合是通过特定的多项式运算规则来实现的。

整个MixColumn变换和相关多项式运算的设计是建立在对现代密码学中扩散和混淆原理的深刻理解之上，通过这种方式，AES确保了即使攻击者拥有部分信息，也难以推断出密钥或是明文信息。

# 3. MixColumn变换的深入剖析

## 3.1 MixColumn变换的运算细节

### 3.1.1 状态矩阵的列变换原理

在AES算法中，状态矩阵的每一列可以被视为一个多项式，而这些多项式在有限域GF(2^8)内进行运算。MixColumn变换涉及到状态矩阵中每一列的线性变换，其目的主要是确保数据之间的扩散，从而增加密码学分析的难度，提高加密的安全性。

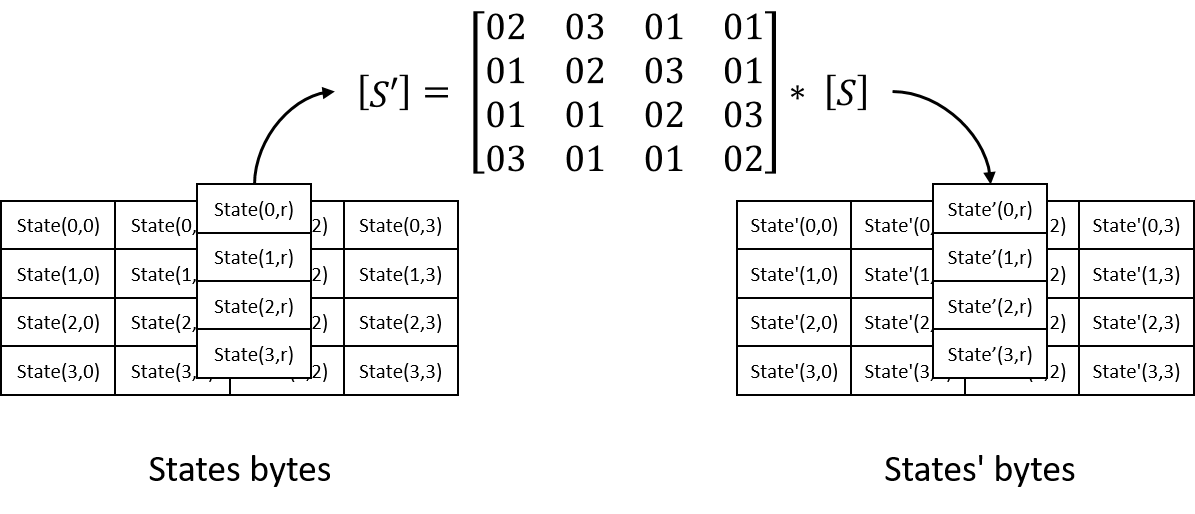
MixColumn变换可表示为：

| b0, b4, b8,  b12 |   | 02 03 01 01 |   | s0, s4, s8,  s12 |
| b1, b5, b9,  b13 | * | 01 02 03 01 | = | s1, s5, s9,  s13 |
| b2, b6, b10, b14 |   | 01 01 02 03 |   | s2, s6, s10, s14 |
| b3, b7, b11, b15 |   | 03 01 01 02 |   | s3, s7, s11, s15 |

上式中，每一个元素`bi`和`sj`都是在GF(2^8)中的字节。乘法和加法运算也都在这个有限域内进行。

MixColumn变换中的系数矩阵（[02 03 01 01]，[01 02 03 01]，[01 01 02 03]，[03 01 01 02]）都遵循特定的数学规则，确保变换是可逆的，以便在解密过程中可以准确地恢复原始数据。

### 3.1.2 系数矩阵的构造及其意义

在MixColumn变换中，系数矩阵的选择对于算法的性能和安全性具有决定性作用。这些系数是精心挑选的，以保证其数学属性能够满足加密的需求。例如，系数矩阵的每行元素都是GF(2^8)中的一个多项式，并且这些多项式都具有特定的“最大公因数”，即它们都是同一个多项式的倍数，但互不相同。

系数矩阵中的每一个元素都对应于一个2x2的矩阵，当它用于变换时，实质上是将状态矩阵中的每个元素乘以对应的2x2矩阵。这种构造方式确保了每次操作都是可逆的，因为这些2x2矩阵的逆在有限域内也是存在的。

### 3.2 MixColumn变换的数学分析

#### 3.2.1 有限域内的乘法运算规则

在GF(2^8)有限域内进行乘法运算时，由于模不可被2整除，所以需