AES加密之MixColumn变换:揭秘性能优化的核心技巧
发布时间: 2024-12-15 23:49:35 阅读量: 11 订阅数: 11 

参考资源链接:[AES加密算法:MixColumn列混合详解](https://wenku.csdn.net/doc/2rcwh8h7ph?spm=1055.2635.3001.10343)
# 1. AES加密算法与MixColumn变换概述
## 1.1 对称加密与AES特点
对称加密算法使用相同的密钥进行数据的加密与解密操作。高级加密标准(AES)是一种广泛使用的对称加密算法,它在安全性、效率和硬件与软件的实现上均表现出色。AES成为现代加密应用的首选标准,其特点在于固定块大小(128位)、可变的密钥长度(128、192、256位)以及出色的性能。
## 1.2 AES的轮次与操作
AES加密算法采用多轮迭代的方式处理数据,包括SubBytes、ShiftRows、MixColumns和AddRoundKey四个基本操作,它们共同构成了AES的主体。每一轮中的操作对数据块进行处理,逐步增加数据的复杂度和混淆程度,确保加密后的数据难以破解。
## 1.3 MixColumn变换的必要性
MixColumn变换是AES加密算法中增加数据复杂度的关键步骤之一。通过数学上的矩阵乘法,它对数据块的每一列进行操作,将列元素混合,从而在加密过程中引入了较高的扩散效果。这种变换对于提高加密的整体安全性至关重要,因为它使得密钥的每一比特变动都会影响到整个数据块的多个比特,从而提供了强大的抗击差分分析的能力。
AES算法的这种设计让其在各种应用场景中,包括资源受限的嵌入式系统和高吞吐量的网络应用,都具备了出色的实用性和性能。本文后续章节将深入探讨MixColumn变换的细节和优化方法,帮助理解AES的加密机制以及如何提高其性能。
# 2. MixColumn变换的理论基础
### 2.1 AES加密算法的结构
#### 2.1.1 对称加密与AES特点
对称加密是加密和解密使用相同密钥的加密方法。高级加密标准(AES)是目前广泛使用的对称加密算法之一。AES具有以下特点:
1. **高效性**:AES算法设计复杂度适中,能够高效地执行加密和解密操作。
2. **安全性**:AES提供了较高的安全性,即使在当前技术条件下,也没有发现有效的攻击方法可以破解。
3. **灵活性**:AES支持不同长度的密钥(如128、192和256位),使它适用于不同的安全需求。
4. **简洁性**:算法结构清晰,易于理解和实现。
#### 2.1.2 AES的轮次与操作
AES加密过程包括多轮迭代,每轮包含以下四个基本操作:
1. **AddRoundKey(轮密钥加)**:将轮密钥与状态矩阵进行逐字节异或操作。
2. **SubBytes(字节替换)**:通过S盒对状态矩阵中的每个字节进行替换。
3. **ShiftRows(行移位)**:对状态矩阵中的行进行循环移位操作。
4. **MixColumns(列混淆)**:对状态矩阵中的列进行数学变换。
在最后一轮,由于MixColumns操作不增加额外的混淆,因此省略了该步骤。
### 2.2 MixColumn变换的工作原理
#### 2.2.1 列混淆的数学背景
MixColumns变换基于有限域上的数学运算。在AES中,每个字节被视为有限域 GF(2^8) 上的一个多项式。列混淆操作对状态矩阵的每一列应用一个固定系数矩阵,并进行多项式乘法。
该变换表达式可以表示为:
\[ S_{column}(x) = { 03 } \times x^{ 3 } + { 01 } \times x^{ 2 } + { 01 } \times x + { 02 } \]
这里的03, 01, 和 02是多项式的系数,在二进制表示下,这些系数可以转换为对应的字节,以便于在有限域上进行操作。
#### 2.2.2 MixColumn在AES中的作用
MixColumns变换的作用是增加混淆,它使得每一列的状态依赖于所有四个输入字节。这样的混合操作确保了输出状态与输入状态之间的高度非线性关系,从而增强了加密的安全性。
### 2.3 MixColumn变换的性能考量
#### 2.3.1 加密速度的影响因素
影响MixColumns变换速度的因素包括:
1. **硬件能力**:处理器的性能和指令集对加密速度有直接影响。
2. **软件优化**:算法实现方式以及是否采取优化策略。
3. **并行计算能力**:在现代多核处理器中,能够有效利用并行计算能力的实现方式可以显著提高速度。
#### 2.3.2 硬件与软件实现的效率差异
硬件实现通常比软件实现更快,主要因为它能够利用专用的硬件电路直接支持加密操作。而软件实现虽然灵活,但受限于通用CPU架构的处理速度。
在软件实现中,MixColumns变换可以通过优化算法来提高效率,例如使用查找表(LUT)等技术。
### 2.3.3 MixColumns变换的性能考量表格
| 性能考量 | 说明 |
| --------- | ---- |
| 硬件加速 | 利用专用硬件电路加速特定计算任务 |
| 代码优化 | 使用算法优化技术提高软件执行效率 |
| 并行处理 | 利用多核处理器并行执行任务以提升性能 |
为了说明硬件加速与软件优化之间的性能差异,可以使用以下代码块进行对比。
```c
// MixColumns变换的传统软件实现(伪代码)
for (int i = 0; i < Nb; i++) {
// 执行列混淆操作
MixColumn(state_column);
}
// MixColumns变换的硬件加速版本(伪代码)
// 通常在拥有AES-NI指令集的处理器上执行
for (int i = 0; i < Nb; i++) {
// 使用AES-NI指令执行列混淆操作
_mm_aesenc_si128(state_column, key_schedule[i]);
}
```
以上代码块展示了一个简单的性能考量,传统软件实现与硬件加速实现的区别在于后者利用特定的硬件指令进行操作,这通常能带来性能上的显著提升。
在下一章节中,我们将深入探讨MixColumn变换的实践优化方法,包括传统的实现方法和优化技巧。
# 3. MixColumn变换的实践优化
## 3.1 MixColumn变换的传统实现方法
### 3.1.1 矩阵乘法的直接实现
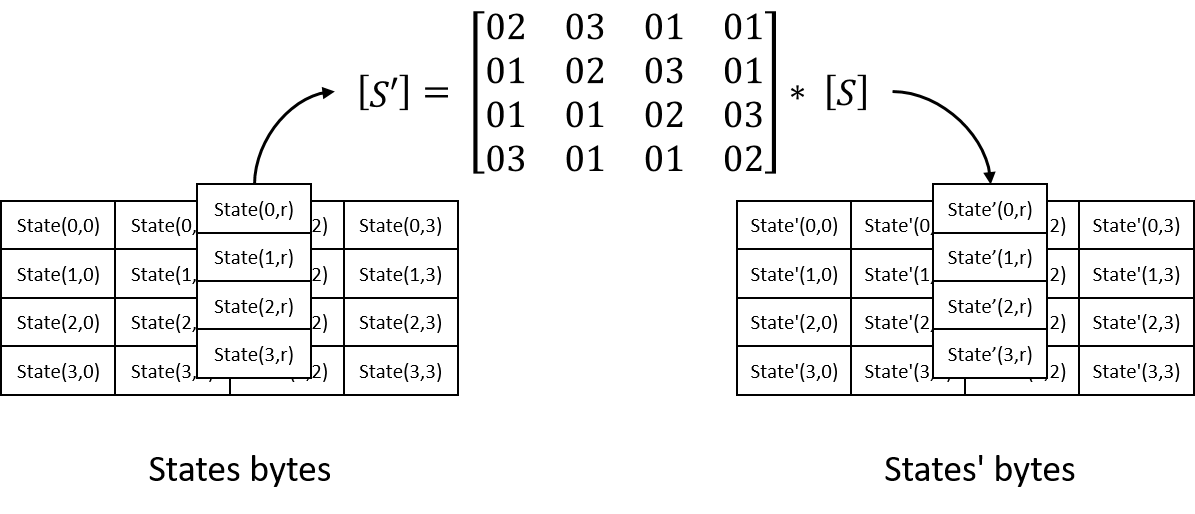
在 AES 算法中,MixColumn 变换是对状态矩阵进行列混淆操作,其中状态矩阵是由待加密的明文或密文块构成的 4x4 字节矩阵。该变换通过一个固定的 4x4 矩阵与状态矩阵相乘来实现。矩阵乘法在数学上可以表示为以下公式:
```
| s0,0 s0,1 s0,2 s0,3 | | 02 03 01 01 | | s'0,0 s'0,1 s'0,2 s'0,3 |
| s1,0 s1,1 s1,2 s1,3 | * | 01 02 03 01 | = | s'1,0 s'1,1 s'1,2 s'1,3 |
| s2,0 s2,1 s2,2 s2,3 | | 01 01 02 03 | | s'2,0 s'2,1 s'2,2 s'2,3 |
| s3,0 s3,1 s3,2 s3,3 | | 03 01 01 02 | | s'3,0 s'3,1 s'3,2 s'3,3 |
```
其中,s*i*,j 表示原始状态矩阵中的字节,s'*i*,j 表示变换后状态矩阵中的字节。矩阵中的数字是十六进制数。
在编程语言中实现矩阵乘法需要对字节进行循环操作,以下是使用 C 语言实现 MixColumn 变换的示例代码:
```c
void mix_column(unsigned char state[4][4]) {
unsigned char a[4], b[4];
for (int col = 0; col < 4; col++) {
a[0] = state[0][col];
a[1] = state[1][col];
a[2] = state[2][col];
a[3] = state[3][col];
b[0] = GF256_mult(a[0], 0x02) ^ GF256_mult(a[1], 0x03) ^ a[2] ^ a[3];
b[1] = a[0] ^ GF256_mult(a[1], 0x02) ^ GF256_mult(a[2], 0x03) ^ a[3];
b[2] = a[0] ^ a[1] ^ GF256_mult(a[2], 0x02) ^ GF256_mult(a[3], 0x03);
b[3] = GF256_mult(a[0], 0x03) ^ a[1] ^ a[2] ^ GF256_mult(a[3], 0x02);
for (int row = 0; row < 4; row++) {
state[row][col] = b[row];
}
}
}
```
在上述代码中,`GF256_mult` 函数用于在 GF(2^8) 上进行模乘操作。`GF256_mult` 的实现与 AES 的有限域上的乘法有关,这不在本节讨论的范围内,因此不会详细展开。
### 3.1.2 代码优化的常见策略
针对 MixColumn 的传统实现,代码优化可以考虑以下策略:
- **循环展开(Loop Unrolling)**:减少循环的开销,直接通过编写多个独立的计算语句代替循环。
- **临时变量减少**:利用局部变量来存储中间结果,减少重复计算。
- **内联函数(Inline Functions)**:将函数调用替换为函数体本身,减少函数调用的开销。
以上策略可以减少 CPU 指令的数目,提高执行效率。
## 3.2 MixColumn变换的优化技巧
### 3.2.1 查表法的原理和实现
查表法是一种优化 MixColumn 变换的技术,通过预先计算好的查找表(Lookup Table)来替代复杂的矩阵乘法计算。这种方法利用了内存与 CPU 计算速度之间的性能差异,通过牺牲内存空间来换取运算速度。
为了实现查表法,我们需要创建一个 256x4 的查找表。每一行代表了 0-255 值的列混淆结果。以下代码展示了如何使用查表法实现 MixColumn 变换:
```c
unsigned char mix_column_table[256][4];
void generate_mix_column_table(void) {
for (int i = 0; i < 256; i++) {
mix_column_table[i][0] = GF256_mult(0x02, i) ^ GF256_mult(0x03, (i >> 7)) ^ (i >> 6) ^ (i >> 5);
mix_column_table[i][1] = GF256_mult(0x02, (i >> 7)) ^ GF256_mult(0x03, i) ^ (i >> 5) ^ (i >> 4);
mix_column_table[i][2] = GF256_mult(0x2, (i >> 6)) ^ GF256_mult(0x3, (i >> 7)) ^ (i >> 4) ^ (i >> 3);
mix_column_table[i][3] = GF256_mult(0x3, (i >> 7)) ^ GF256_mult(0x2, i) ^ (i >> 3) ^ (i >> 2);
}
}
void mix_column_lookup(unsigned char state[4][4]) {
unsigned char temp[4];
for (int col = 0; col < 4; col++) {
for (int row = 0; row < 4; row++) {
temp[row] = mix_column_table[state[row][col]][row];
}
for (int row = 0; row < 4; row++) {
state[row][col] = temp[row];
}
}
}
```
在 `generate_mix_column_table` 函数中,我们初始化查表。注意,这里的 `GF256_mult` 函数和前面提到的相同,用于有限域上的乘法运算。
### 3.2.2 并行计算与优化
随着现代 CPU 的多核架构,执行并行计算成为提高程序效率的一个重要方面。为了使 MixColumn 变换能够利用并行计算的优势,可以将状态矩阵的列分散到不同的线程中去,然后并行处理这些列。
并行计算的实现可以通过多线程或多进程来完成。在 C 语言中,可以使用 `pthreads` 库来创建和管理线程。
```c
void *mix_column_parallel(void *arg) {
int col = *((int *)arg);
unsigned char *state = (unsigned char *)mix_column_parallel_state;
for (int row = 0; row < 4; row++) {
unsigned char a = state[row * 4 + col];
state[row * 4 + col] = GF256_mult(0x02, a) ^ GF256_mult(0x03, (a >> 7)) ^ (a >> 6) ^ (a >> 5);
}
return NULL;
}
void mix_column_parallel(unsigned char state[4][4]) {
pthread_t threads[4];
int arg[4] = {0, 1, 2, 3};
for (int i = 0; i < 4; i++) {
pthread_create(&threads[i], NULL, mix_column_parallel, (void *)&arg[i]);
}
for (int i = 0; i < 4; i++) {
pthread_join(threads[i], NULL);
}
}
```
在上述代码中,`mix_column_parallel` 函数创建了四个线程,每个线程负责处理状态矩阵的一列。
## 3.3 MixColumn变换的性能测试
### 3.3.1 测试环境的搭建
为了测试 MixColumn 变换的性能,需要设置一个适合的测试环境。这个环境应该包括:
- **硬件**:性能均衡的 CPU,足够的 RAM。
- **操作系统**:稳定的 Linux 发行版或 Windows。
- **编译器**:支持优化选项的编译器,如 GCC 或 MSVC。
- **测试工具**:性能测试软件,如 perf, Intel Vtune 或 Windows Performance Analyzer。
搭建测试环境时,需要确保系统的其他进程不会影响测试结果。测试工具应该能够测量 MixColumn 变换函数的执行时间,CPU 使用率,以及可能的缓存命中率等性能指标。
### 3.3.2 性能评估与分析
性能评估与分析是优化过程中的关键环节。通过测试数据可以了解当前算法实现的性能瓶颈,以及优化措施的效果。以下是一些性能评估的步骤:
- **执行时间测量**:记录优化前后 MixColumn 变换的执行时间,比较它们的差异。
- **指令计数**:使用如 `perf` 的工具来统计 CPU 执行的指令数目。
- **缓存命中分析**:分析代码对 CPU 缓存的使用效率,如数据是否在 L1/L2/L3 缓存中命中。
- **并行度分析**:对于并行计算,应测量并行代码的扩展性和效率。
性能评估可能需要多次迭代,每次迭代根据分析结果对代码进行调整,以达到更优的性能。
由于篇幅限制,第三章的其他部分和后续章节无法在此展示,但上述内容涵盖了3.1至3.3小节的内容。在后续章节中,将深入探讨 AES 加密优化的高级策略,并通过案例研究,展示 MixColumn 变换优化实例的分析和总结。
# 4. AES加密优化的高级策略
## 4.1 硬件加速技术
### 4.1.1 AES指令集(AES-NI)的介绍
AES-NI是Intel在2010年引入的一组指令集扩展,旨在提高AES加密和解密操作的效率。这个指令集包括了执行AES加密、解密、密钥扩展和其他相关操作的指令。通过直接在处理器级别实现这些操作,AES-NI显著降低了进行AES操作所需的周期数,从而提高了性能并减少了CPU资源的占用。
在AES-NI支持的CPU上执行AES操作比传统的软件实现要快得多,因为它利用了专门的硬件电路来执行特定的计算,这些计算在软件中执行会涉及到复杂的数组操作和位操作。使用AES-NI可以减少能耗,提升加密操作的速度,特别适合需要大量加密/解密操作的应用场景,比如云服务和大数据处理。
### 4.1.2 AES-NI在MixColumn中的应用
在AES算法的MixColumn操作阶段,AES-NI指令集提供了一些非常有用的指令,它们能够直接对数据块的各个列进行操作,这样就可以直接在硬件层面上进行列混淆,而不是通过软件层面的复杂计算。
具体来说,`AESENC` 和 `AESENCLAST` 指令可以用来对数据块执行单轮或多轮的加密操作,而`AESDEC` 和 `AESDECLAST` 则用于解密。使用这些指令可以显著简化代码,提高效率。例如,在执行MixColumn操作时,传统实现可能需要多个步骤来构建变换矩阵并执行矩阵乘法。利用AES-NI,这些步骤可以被简化为几条指令的调用。
```assembly
; 示例代码片段:使用AES-NI指令集进行AES加密
aesenc %r10, %r11 ; 第一轮加密
aesenc %r12, %r11 ; 第二轮加密
aesenc %r13, %r11 ; 第三轮加密
aesenc %r14, %r11 ; 第四轮加密
aesenc %r15, %r11 ; 第五轮加密
aesenc %r16, %r11 ; 第六轮加密
aesenc %r17, %r11 ; 第七轮加密
aesenc %r18, %r11 ; 第八轮加密
aesenc %r19, %r11 ; 第九轮加密
aesenc %r20, %r11 ; 第十轮加密
aesenclast %r21, %r11 ; 最后一轮加密
```
这个例子展示了如何使用`aesenc`指令执行多个加密轮次。每条指令执行一轮,最后一条执行最后一轮。`aesenclast`指令执行最后一轮加密操作,它和普通的`aesenc`指令有轻微的不同,以确保最终输出是正确的。
## 4.2 软件优化技巧
### 4.2.1 编译器优化选项
编译器优化选项是提升代码性能的重要手段。对于加密算法,特别是像AES这样的对性能要求极高的算法,正确使用编译器优化选项可以显著提高执行速度和效率。常见的编译器优化选项包括:
- **O2/O3**:这两个选项是GCC/Clang编译器中常用的优化级别,它们会启用包括循环展开、函数内联等优化技术,减少程序运行时的开销。
- **Ofast**:比O3更进一步,它允许进行一些不改变程序数学属性的优化。
- **march=native**:让编译器为当前运行代码的CPU架构生成最优代码。
- **fp-model fast=2**:在支持编译器上,此选项将启用对浮点运算的特殊优化。
使用这些优化选项时,开发者应该了解它们的具体行为和可能对程序产生的影响。特别是对于加密算法而言,有些优化可能会引入数值计算上的误差,这在安全敏感的应用中是不允许的。
例如,在编译优化级别为O2的情况下,编译器会进行如下优化:
- 移除未使用的函数和变量。
- 优化循环,包括循环展开、循环测试的优化等。
- 尽可能地内联小函数。
- 重新排序指令以减少处理器的延迟。
### 4.2.2 高级编程语言中的优化
虽然高级编程语言如Python、Java等在性能上无法与C/C++等语言相比,但它们在开发效率和跨平台方面具有明显优势。因此,针对这些语言的优化策略也是十分必要的。优化高级编程语言中的AES加密算法,通常包括以下几个方面:
- **算法优化**:对于Python等动态类型语言,可以使用静态类型注解来加快运行时类型推断的速度。
- **库优化**:使用专门的加密库,如Python中的`cryptography`库,这些库内部已经进行了优化。
- **编译为本地代码**:使用工具如PyInstaller将Python代码编译为本地机器码,从而加快执行速度。
- **并行计算**:使用多线程或异步IO来提高计算密集型任务的性能。
在实现AES加密时,选择合适的数据结构和算法结构也非常重要。例如,在Python中,可以使用`bytearray`来代替`bytes`,因为`bytearray`提供了更多的操作方法,且在很多情况下有更好的性能表现。
```python
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
from cryptography.hazmat.backends import default_backend
# 示例代码片段:使用cryptography库进行AES加密
def encryptAES(data: bytearray, key: bytearray):
backend = default_backend()
cipher = Cipher(algorithms.AES(key), modes.CBC(b'\x00'*16), backend=backend)
encryptor = cipher.encryptor()
return encryptor.update(data) + encryptor.finalize()
```
在这个Python示例中,我们使用了`cryptography`库的`Cipher`类进行加密操作。这种库提供了优化后的实现,并且易于使用,但开发者应该注意检查库文档,确保库的实现方式满足自己的安全性要求。
## 4.3 安全与优化的平衡
### 4.3.1 优化对安全性的影响
优化代码时,特别是在涉及加密算法的情况下,开发者必须格外注意安全性的保持。优化可能会引入新的漏洞,或使得现有漏洞更容易被利用。例如:
- **缓冲区溢出**:在执行优化,尤其是手动优化时,开发者可能会错误地管理内存缓冲区,从而导致缓冲区溢出漏洞。
- **时间攻击**:某些优化可能会暴露时间差异,恶意用户可以利用这些差异来获取有关加密密钥的信息。
- **密钥空间泄露**:优化后的代码可能会无意中减少密钥空间,从而降低加密的强度。
因此,开发者必须在优化和安全性之间找到一个平衡点,特别是在对性能有极高要求的场合。对加密算法进行优化时,应当遵循如下原则:
- **不改变算法的数学属性**:优化不应影响加密操作的数学基础和结果。
- **保持操作一致性**:优化不能改变数据处理的逻辑,以避免引入新的漏洞。
- **测试与验证**:任何优化后都需要进行彻底的安全测试,以确保没有引入安全漏洞。
### 4.3.2 寻找优化与安全的平衡点
找到优化与安全之间的平衡点是加密算法实现中的重要任务。为了实现这一平衡,开发者可以采取以下措施:
- **使用经过验证的库**:使用经过广泛测试和审计的加密库,而不是自己实现算法。这些库通常由专家维护,并且已经考虑到了安全性和性能。
- **开启编译器安全选项**:一些编译器提供了用于提高代码安全性的选项,比如GCC的`-D_FORTIFY_SOURCE`选项,这可以在编译时进行安全检查。
- **执行动态代码分析**:使用如Valgrind、AddressSanitizer等工具对代码进行运行时分析,确保没有内存安全问题。
- **代码审查**:通过同行审查,可以发现潜在的安全漏洞和性能问题。
- **性能基准测试**:使用专业的性能测试工具,对加密算法的性能进行基准测试,确保优化没有降低性能。
在平衡优化和安全时,还需要进行权衡。开发者应该明确性能目标和安全需求,然后制定相应的优化策略。在某些情况下,牺牲一些性能来获得更强的安全保障是值得的,反之亦然。然而,这两者并不是相互排斥的,很多优化措施可以同时提高性能和安全性。例如,使用AES-NI指令集不仅提高了性能,同时也由于其硬件实现的特性,提高了抵抗侧信道攻击的能力。
# 5. 案例研究:MixColumn变换的优化实例
在现代信息安全领域,对加密算法的优化不仅仅是理论上的探讨,更多的是为了在现实世界中的应用场景提供效率和安全的保障。本章将以MixColumn变换为例,分析并展示不同优化方法在实际应用中的效果对比,包括硬件加速与软件优化的性能对比,以及在不同应用场景下的性能优化策略。通过对这些案例的分析,我们将总结出成功的要素,并展望未来优化的方向。
## 5.1 实例分析:不同优化方法的效果对比
### 5.1.1 传统方法与优化方法的比较
传统的MixColumn变换通常使用矩阵乘法进行实现,这种方法在理论上是清晰的,但在实际执行时却可能面临效率的挑战。以下是一个简化的传统MixColumn变换的矩阵乘法实现示例:
```c
void traditional_mix_column(uint8_t state[4]) {
uint8_t a[4], b[4], c[4];
// ... 假设a是原始状态,b是混合后的状态 ...
for (int i = 0; i < 4; i++) {
c[i] = gmult(a[0], 0x02) ^ gmult(a[1], 0x03) ^ a[2] ^ a[3]; // 假设gmult是有限域上的乘法函数
// ... 对于每个列进行类似的操作 ...
}
// 将b设置为新的状态
memcpy(b, c, 4);
}
```
而优化方法,如查表法,通过预计算的方式显著减少了运算量:
```c
void optimized_mix_column(uint8_t state[4]) {
static const uint8_t mix_column_table[256] = {
// 预计算的混合列表...
};
for (int i = 0; i < 4; i++) {
state[i] = mix_column_table[state[i]]; // 直接查表替代矩阵乘法
}
}
```
查表法通过牺牲内存空间来换取计算时间,但这种优化在现代计算机体系结构中通常是值得的,因为它能够极大提升处理速度。
### 5.1.2 硬件加速与软件优化的性能对比
硬件加速和软件优化是两种不同的性能提升途径。在硬件层面上,AES-NI指令集提供了一种特别设计的硬件支持,能够在处理器级别上直接执行AES加密操作,从而大大加快了加密速度。以下是一个使用AES-NI指令集的例子:
```asm
# 示例代码展示如何使用AES-NI指令集进行加密操作
# 这里假设使用的是Intel架构的汇编指令
vmovdqu ymm0, [rdx] ; 将状态加载到寄存器
vpclmulqdq ymm1, ymm0, ymmword ptr [rcx], 0x00 ; 执行MixColumn变换
vmovdqu [rdx], ymm1 ; 存储新状态
```
软件优化,例如编译器优化选项,可以利用现代编译器的高级优化技术。使用`-O3`编译选项通常能够让编译器进行更为激进的优化,提高执行速度和减少资源消耗。
性能对比通常需要在测试环境下进行,通过实际测量来确定不同优化方法的效果。
## 5.2 应用场景下的性能优化
### 5.2.1 实时加密场景的优化考虑
在需要进行实时数据加密的场景,如视频流加密或金融交易加密,性能优化显得尤为重要。由于数据需要在极短的时间内完成加密,因此对算法的效率要求极高。
对于这类场景,需要综合考虑硬件加速和软件优化的结合使用。例如,在支持AES-NI的处理器上,将MixColumn变换交给硬件执行,同时对其他算法步骤进行软件层面的优化。
### 5.2.2 低资源消耗设备的加密策略
在资源受限的环境下,例如物联网设备或移动设备,需要在保持安全性的同时减少资源消耗。在这种情况下,优化策略可能需要牺牲一定的速度来换取更低的资源使用。
例如,在某些情况下,可以使用一种轻量级的加密算法作为替代方案,或者在算法中采用更小的密钥长度来减少计算需求。
## 5.3 案例总结与启示
### 5.3.1 案例的成功要素分析
本章通过具体案例分析了不同优化方法在实际中的应用效果。成功要素主要包括:
1. 理解应用场景需求:了解加密算法将被应用在什么类型的场景中,这将决定优化的方向和重点。
2. 选择适当的优化技术:无论是硬件加速还是软件优化,选择适合特定场景的技术至关重要。
3. 综合多种优化策略:通过结合不同的优化手段,达到最佳的性能和安全性平衡。
4. 持续的测试与评估:优化效果需要通过实际测试来验证,并根据测试结果不断调整优化策略。
### 5.3.2 未来优化方向的展望
未来优化方向可以朝着以下几个方向发展:
1. 高效的轻量级算法研究:随着物联网设备的普及,对轻量级加密算法的需求越来越高。
2. 量子计算的适应性:研究加密算法如何适应量子计算环境,提高抗量子攻击的能力。
3. 自适应算法:根据实际运行环境动态调整加密算法的执行策略,以实现最佳的性能和安全性。
通过不断的研究和实验,我们可以进一步提升AES加密算法,特别是MixColumn变换的性能和效率,在保证安全的前提下满足未来多样化的需求。
# 6. 总结与展望
在前几章节中,我们深入探讨了AES加密算法中的MixColumn变换,从理论基础、实践优化到高级策略,再到实际案例分析。在此基础上,本章将对这些内容进行汇总,重点回顾MixColumn变换优化的关键点,并展望加密算法优化的未来趋势。
## 6.1 MixColumn变换优化的总结
### 6.1.1 优化实践的关键点回顾
在MixColumn变换的优化实践中,我们从多个角度对传统实现方法进行了改进。首先,在传统的矩阵乘法实现中,通过代码优化,我们尝试了减少乘法和加法操作的次数,避免不必要的内存访问,以及使用更高效的算法结构,如查找表(Lookup Table)和并行计算。
以查找表优化为例,通过预先计算列混淆操作中可能出现的所有结果,并将它们存储在查找表中,从而在执行时能够通过索引直接访问结果,这大大减少了运算时间。此外,现代处理器的向量化指令集(如SSE和AVX)能够对数据进行批量处理,进一步提升了MixColumn变换的性能。
### 6.1.2 理论与实践结合的价值
理论研究为实践提供了坚实的基础。在理论层面,我们分析了MixColumn变换的数学原理,揭示了它在AES加密中的重要性。在实践层面,理论的指导使得优化策略更加有的放矢。例如,了解列混淆操作如何影响轮次的输出,让我们能够设计出更高效的算法实现和优化方案。
结合理论与实践,我们不仅提升了算法效率,还确保了在优化过程中不损害加密的安全性。实践中得出的宝贵经验,又反哺理论研究,推动了加密技术的持续进步。
## 6.2 加密算法优化的未来趋势
### 6.2.1 新兴技术与加密优化
随着硬件技术的快速发展,特别是量子计算和人工智能的发展,加密算法优化将面临新的机遇与挑战。量子计算有望在理论上打破现有的加密体系,但同时也推动了后量子加密算法的研究,旨在构建能够抵抗量子攻击的加密技术。
另一方面,人工智能的算法优化能力可以应用于加密算法的自适应调整,使算法能够在特定的硬件和软件环境中找到最优的性能表现。例如,机器学习算法能够分析大量加密操作的数据,从而发现性能瓶颈并提出改进措施。
### 6.2.2 持续优化与安全挑战
优化是一个持续的过程。随着攻击技术的发展和加密算法的广泛部署,优化工作需要不断适应新的威胁环境。安全研究人员必须不断寻找潜在的漏洞,并通过优化手段来加以修补。例如,侧信道攻击揭示了物理信息泄露的可能性,从而推动了对加密算法实现方式的深入研究和改进。
此外,随着物联网(IoT)设备的普及,对轻量级加密算法的需求日益增长。在保证安全的前提下,优化这些算法以适应资源受限的环境,将是未来研究的重点方向之一。
总之,MixColumn变换的优化不仅加深了我们对AES加密算法的认识,也为我们提供了处理更广泛加密问题的思路和方法。未来,随着技术的发展,我们将继续在优化与安全之间寻找平衡,推动加密技术的进步。
0
0






