【fsolve的限制与挑战】：面对高难度问题时的策略与方法


参考资源链接：[MATLAB fsolve函数详解：求解非线性方程组](https://wenku.csdn.net/doc/6471b45dd12cbe7ec3017515?spm=1055.2635.3001.10343)
# 1. fsolve基本概述与应用场景

## 1.1 fsolve简介
`fsolve`是MATLAB中用于求解非线性方程组的函数。它采用牛顿法、拟牛顿法等算法，能够高效地找到方程或方程组的根。该工具在工程计算、科学研究、数据分析等多个领域有着广泛的应用。

## 1.2 应用场景
fsolve的应用场景包括但不限于以下几个方面：
- **工程设计**：在机械设计、电路分析等领域用于求解复杂的非线性系统。
- **科学研究**：在物理、化学等学科中，用于解决模型中出现的非线性方程。
- **数据分析**：在统计分析、机器学习等领域，用于优化问题的求解。

## 1.3 fsolve使用示例
假设我们要解决以下非线性方程组：
\[ f(x, y) = \begin{cases}
3x^2 - y^2 = 0 \\
x^2 + y = 1
\end{cases} \]

在MATLAB中，首先定义方程组：

function F = myfun(x)
    F = [3*x(1)^2 - x(2)^2; x(1)^2 + x(2) - 1];
end

然后使用`fsolve`进行求解：

x0 = [0.5, 0.5]; % 初始猜测值
[x, fval, exitflag, output] = fsolve(@myfun, x0);

以上代码会输出方程组的根，并且包含了关于求解过程的详细信息。

fsolve作为解决非线性问题的强大工具，其应用远不止于此，更多高级使用技巧和场景将在后续章节中深入探讨。

# 2. fsolve算法的理论基础

## 2.1 数学模型与问题表达

### 2.1.1 高难度问题的数学描述

在面对现实世界的复杂问题时，数学模型提供了一种将其抽象化、量化的有效手段。对于高难度问题，尤其是那些无法直接通过解析方法求解的问题，数学建模成为了获取解决方案的必要途径。

考虑一个非线性系统，其数学模型可表示为一组方程组：

\[ F(x) = \begin{bmatrix} f_1(x_1, x_2, \ldots, x_n) \\ f_2(x_1, x_2, \ldots, x_n) \\ \vdots \\ f_n(x_1, x_2, \ldots, x_n) \end{bmatrix} = \mathbf{0} \]

这里，\( F \) 为 \( n \) 维向量函数，\( x \) 为变量向量，且每一项 \( f_i \) 都是非线性的。求解这类方程组以找到 \( x \) 使得 \( F(x) \) 为零，即求解 \( x \) 使得系统达到某种平衡或稳定状态。

在高难度问题中，可能涉及非线性、不连续、甚至不确定性因素，从而对传统的解析方法提出了挑战。例如，在化学反应模型、流体动力学以及结构力学等问题中，非线性特征显著，并且通常需要借助数值方法来求解。

### 2.1.2 非线性系统与优化问题

非线性系统中存在诸多不确定性和复杂性，使得传统线性方法无法直接应用。非线性系统中的优化问题往往难以求得全局最优解，因为非线性函数可能拥有多个局部极值点。这导致优化问题不仅要找出解，还需要确定解的类型（全局极值或局部极值）。

在优化问题中，目标函数可以描述为：

\[ \min_{x \in \mathbb{R}^n} f(x) \]

其中，\( f(x) \) 是非线性函数。该问题的解可能位于函数的鞍点、局部最小点，或者全局最小点。求解这类问题需要采用梯度下降法、遗传算法、模拟退火等启发式算法，或是结合fsolve进行求解。

## 2.2 fsolve算法原理与实现

### 2.2.1 算法的核心思想

fsolve 算法，常用于求解无约束非线性方程组的根。核心思想是利用迭代方法逐渐逼近方程的解，直至满足预定的误差范围或达到最大迭代次数。

算法迭代公式通常采用：

\[ x^{(k+1)} = x^{(k)} + \Delta x \]

其中，\( x^{(k)} \) 表示第 \( k \) 次迭代的结果，\( \Delta x \) 表示迭代步长或修正项。步长的选取至关重要，过小会导致收敛速度慢，过大则可能使迭代过程发散。

### 2.2.2 关键步骤的详细解析

fsolve 算法的核心步骤包括：

1. **初始猜测**：选择一个合适的初始猜测值 \( x^{(0)} \)。初始值对收敛性有很大影响。
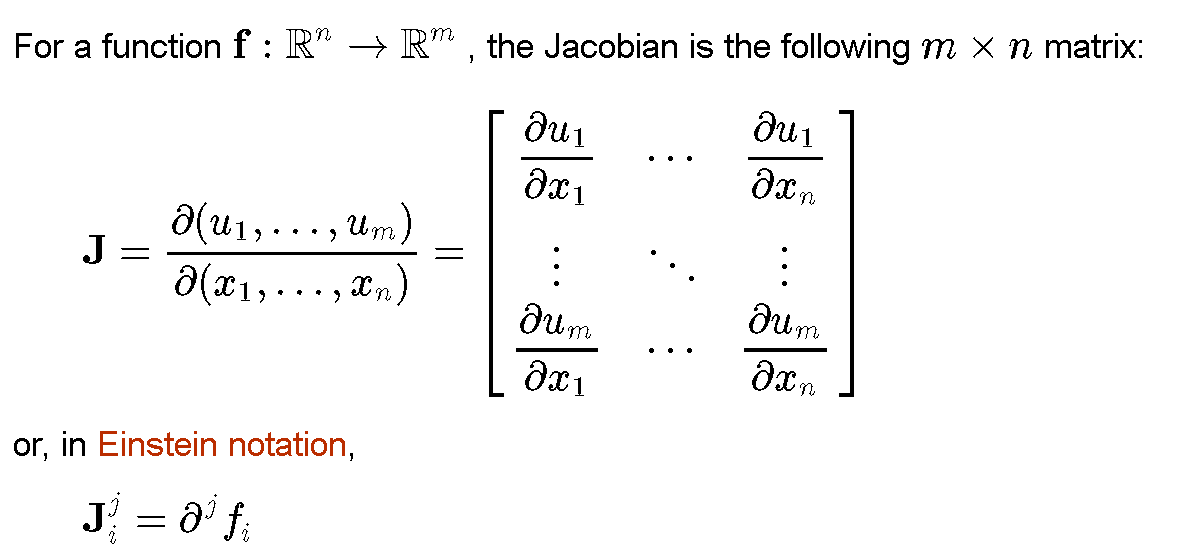
2. **线性近似**：将非线性函数 \( F(x) \) 在当前点 \( x^{(k)} \) 处进行线性近似，得到雅可比矩阵 \( J(x^{(k)}) \)。
3. **求解线性方程组**：求解线性方程组 \( J(x^{(k)}) \Delta x = -F(x^{(k)}) \) 得到修正项 \( \Delta x \)。
4. **更新解**：更新 \( x^{(k+1)} = x^{(k)} + \Delta x \) 并检查是否满足收敛条件。

### 2.2.3 算法的限制因素

尽管fsolve在许多情况下都很有效，但它并非万能。其限制因素主要来自：

- **初值选择**：如果初始猜测值距离真实的解太远，算法可能无法找到正确的解。
- **雅可比矩阵的奇异性**：当雅可比矩阵 \( J(x) \) 奇异或接近奇异时，可能无法求解线性方程组，导致算法失效。
- **局部极值问题**：fsolve可能收敛到方程组的局部极值而非全局最优解。
- **计算资源**：求解雅可比矩阵和线性方程组可能需要大量的计算资源。

fsolve算法的具体实现涉及多个步骤和策略，接下来，我们从代码实现的角度深入了解其工作原理。

# 3. fsolve实践中的常见挑战

## 3.1 初始猜测值的重要性与选择策略

### 初始猜测值对收敛性的影响

在fsolve算法的应用中，初始猜测值的选择对于算法能否快速收敛至正确解具有决定性的作用。选择一个接近真实解的初始猜测值，可以显著减少迭代次数，加快求解速度。而一个不当的初始猜测值可能导致算法迭代失败，甚至发散，使得求解过程无法完成。

假设在求解非线性方程组时，方程组的解分布在解空间的不同区域，初始猜测值若选择在远离解的区域，fsolve算法的迭代过程会消耗更多的时间，甚至可能因为远离解的初始猜测值而导致无法找到任何解。

### 如何有效选取初始猜测值

选取初始猜测值并没有绝对的规则，但是在实践中，我们可以通过以下方法来提高初始猜测值的准确性：

- **领域知识**：在具体问题领域中，研究者往往能够根据经验和直觉选取一个较为合理的初始猜测值。
- **实验分析**：通过在问题的参数空间内进行采样，可以使用图形化的方法来分析解的分布情况，从而帮助我们选择一个好的初始猜测值。
- **数据驱动**：如果问题的历史数据是可用的，那么可以使用这些数据来估计一个较好的初始猜测值。

在编程实现上，我们也可以通过编写代码来对初始猜测值进行优化。以下是使用Python的示例代码，说明如何通过探索性数据分析选择一个合理的初始猜测值：

import numpy as np
import matplotlib.pyplot as plt

# 假设我们有历