【多项式分解的艺术】：揭秘分解奥秘，掌握数学难题利器

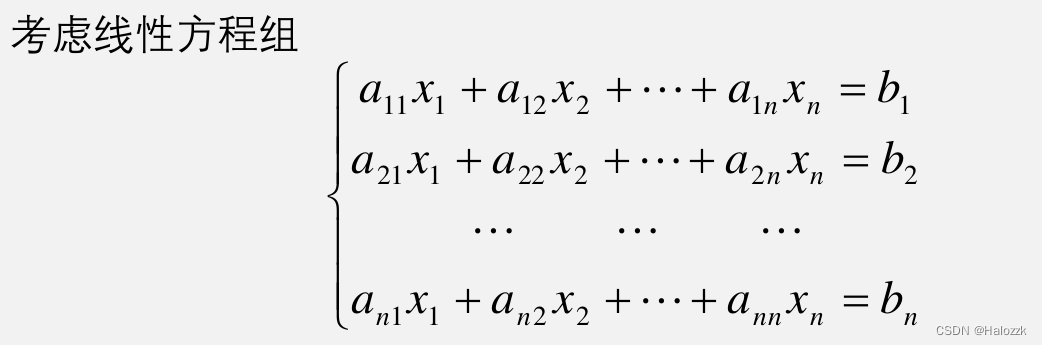
# 1. 多项式分解的基本原理

多项式分解是将一个多项式表示为多个因式的乘积的过程。其基本原理在于将多项式中的公因子提取出来，然后利用因式分解公式将剩余的部分分解为更简单的因式。

**公因式提取**是将多项式中所有项的公因子提取出来，从而得到一个公因子和一个余式。例如，多项式 `2x^2 + 4x + 6` 可以提取出公因子 `2`，得到 `2(x^2 + 2x + 3)`。

**因式分解公式**是将多项式分解为更简单的因式的公式。常见的因式分解公式包括差平方公式、完全平方公式和平方差公式。例如，差平方公式 `a^2 - b^2 = (a + b)(a - b)` 可以将多项式 `x^2 - 4` 分解为 `(x + 2)(x - 2)`。

# 2. 多项式分解的技巧

### 2.1 因式分解

因式分解是将一个多项式分解为几个因式的过程。它可以帮助我们化简多项式、求解方程、证明数学定理等。下面介绍几种常见的因式分解技巧。

#### 2.1.1 公因式提取

**原理：**如果一个多项式中的每一项都有一个公因子，则可以将这个公因子提取出来，得到一个新的多项式。

**步骤：**

1. 找出多项式中所有项的公因子。
2. 将公因子提取出来，得到一个新的多项式。

**示例：**

多项式：x^2 - 2x + 1
公因子：x
提取公因子：x(x - 2 + 1) = x(x - 1)

#### 2.1.2 差平方公式

**原理：**差平方公式可以将一个多项式分解为两个因式的差的平方。

**公式：**

a^2 - b^2 = (a + b)(a - b)

**步骤：**

1. 将多项式写成两个项的平方差的形式。
2. 应用差平方公式，得到两个因式的差。

**示例：**

多项式：x^2 - 4
差平方公式：x^2 - 4 = (x + 2)(x - 2)

#### 2.1.3 完全平方公式

**原理：**完全平方公式可以将一个多项式分解为一个二项式的平方。

**公式：**

(a + b)^2 = a^2 + 2ab + b^2
(a - b)^2 = a^2 - 2ab + b^2

**步骤：**

1. 将多项式写成一个二项式的平方和的形式。
2. 应用完全平方公式，得到二项式的平方。

**示例：**

多项式：x^2 + 4x + 4
完全平方公式：(x + 2)^2 = x^2 + 4x + 4

### 2.2 分解为二次因式

#### 2.2.1 平方差公式

**原理：**平方差公式可以将一个多项式分解为两个二次因式的差。

**公式：**

a^2 - b^2 = (a + b)(a - b)

**步骤：**

1. 将多项式写成两个二次项的差的形式。
2. 应用平方差公式，得到两个二次因式的差。

**示例：**

多项式：x^4 - 16
平方差公式：x^4 - 16 = (x^2 + 4)(x^2 - 4)

#### 2.2.2 配方法

**原理：**配方法可以将一个多项式分解为一个二次因式和一个常数。

**步骤：**

1. 将多项式写成一个二次项和一个常数的和的形式。
2. 将二次项补全平方，得到一个二次因式和一个常数。

**示例：**

多项式：x^2 + 6x + 5
配方法：x^2 + 6x + 5 = (x + 3)^2 - 4

### 2.3 分解为高次因式

#### 2.3.1 韦达定理

**原理：**韦达定理可以根据多项式的系数求出它的根。

**定理：**

对于一个 n 次多项式：

f(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0

它的根为：

x_1 + x_2 + ... + x_n = -a_{n-1}/a_n
x_1 x_2 ... x_n = (-1)^n a_0/a_n

**步骤：**

1. 根据韦达定理求出多项式的根。
2. 将根代入多项式，得到高次因式。

**示例：**

多项式：x^3 - 2x^2 + x - 2
韦达定理：x_1 + x_2 + x_3 = 2
x_1 x_2 x_3 = -2
高次因式：(x - 1)(x - 2)

#### 2.3.2 秦九韶算法

**原理：**秦九韶算法是一种求解高次多项式根的算法。

**步骤：**

1. 将多项式写成一个高次项和一个低次项的和的形式。
2. 将高次项的系数除以低次项的系数，得到一个商。
3. 将商的相反数与低次项的系数相乘，得到一个差。
4. 将差与高次项的系数相加，得到一个新的高次项的系数。
5. 将低次项的系数与商相乘，得到一个新的低次项的系数。
6. 重复步骤 2-5，直到得到一个一元二次方程。
7. 求解一元二次方程，得到多项式的根。

**示例：**

多项式：x^4 - 2x^3 + x^2 - 2x + 1
秦九韶算法：
高次项：x^4
低次项：1
商：x^3
差：-2x^3
新高次项系数：x^3 - 2x^3 = -x^3
新低次项系数：1 * x^3 = x^3
一元二次方程：x^2 - 2x + 1 = 0
根：x = 1 ± i

# 3.1 求解方程

多项式分解在求解方程中有着广泛的应用。通过将方程中的多项式分解为因式，我们可以更轻松地求解方程的根。

**步骤：**

1. **分解多项式：**将方程中的多项式分解为因式。
2. **令因式为零：**将每个因式分别令为零，得到一系列方程。
3. **求解方程：**求解每一组方程，得到方程的根。

**示例：**

求解方程：`x^3 - 2x^2 - 5x + 6 = 0`

**分解多项式：**

`(x - 1)(x^2 - x - 6) = 0`

**令因式为零：**

x - 1 = 0
x^2 - x - 6 = 0

**求解方程：**

x = 1

x = 3, -2

因此，方程的根为：`1, 3, -2`。

### 3.2 化简代数表达式

多项式分解还可以用于化简代数表达式。通过将表达式中的多项式分解为因式，我们可以简化表达式的形式，使其更易于求值或理解。

**步骤：**

1. **分解多项式：**将表达式中的多项式分解为因式。
2. **代入因式：**将分解后的因式代入表达式中。
3. **化简表达式：**利用代数运算，化简表达式。

**示例：**

化简表达式：`x^2 - 4xy + 4y^2 - 9`

**分解多项式：**

`(x - 2y)^2 - 9`

**代入因式：**

`x^2 - 4xy + 4y^2 - 9 = (x - 2y)^2 - 9`

**化简表达式：**

`x^2 - 4xy + 4y^2 - 9 = (x - 2y - 3)(x - 2y + 3)`

### 3.3 证明数学定理

多项式分解在证明数学定理中也发挥着重要作用。通过将定理中的多项式分解为因式，我们可以更清晰地理解定理的含义，并推导出更一般的结论。

**步骤：**

1. **分解多项式：**将定理中的多项式分解为因式。
2. **分析因式：**分析分解后的因式，找出它们的性质和关系。
3. **证明定理：**利用分解后的因式，推导出定理的结论。

**示例：**

证明定理：`对于任何正整数n，n^2 + n + 1不是素数`

**分解多项式：**

`n^2 + n + 1 = (n + 1/2)^2 + 3/4`

**分析因式：**

`(n + 1/2)^2`是一个平方项，始终非负。`3/4`是一个正数。因此，`n^2 + n + 1`始终大于1，且不是素数。

**证明定理：**

证毕。

# 4. 多项式分解的进阶方法

### 4.1 格罗布纳基

#### 4.1.1 格罗布纳基的定义和性质

格罗布纳基是多项式理想的一种基，它具有以下性质：

- **唯一性：**对于给定的多项式理想，存在唯一的格罗布纳基。
- **极小性：**格罗布纳基中不包含任何多项式的倍数。
- **归约性：**格罗布纳基中的任何多项式都可以表示为其他多项式的线性组合。
- **正则性：**格罗布纳基中的首项系数均为 1。

#### 4.1.2 格罗布纳基的应用

格罗布纳基在多项式分解中有着广泛的应用，包括：

- **求解方程组：**通过将方程组转化为多项式理想，并计算其格罗布纳基，可以求解方程组的解。
- **化简代数表达式：**通过计算表达式的格罗布纳基，可以化简表达式并提取出隐含的因子。
- **证明数学定理：**通过将定理转化为多项式理想，并计算其格罗布纳基，可以证明或反证定理。

### 4.2 同余分解

#### 4.2.1 同余分解的原理

同余分解是一种将多项式分解为模某个多项式的因子的方法。其原理如下：

设 $f(x)$ 是一个多项式，$g(x)$ 是一个不可约多项式，则存在多项式 $q(x)$ 和 $r(x)$，使得：

$$f(x) = q(x)g(x) + r(x)$$

其中 $r(x)$ 的次数小于 $g(x)$ 的次数。如果 $r(x) = 0$，则称 $f(x)$ 同余于 0 模 $g(x)$。

#### 4.2.2 同余分解的应用

同余分解在多项式分解中有着重要的应用，包括：

- **求解模方程：**通过将模方程转化为同余方程，并利用同余分解求解同余方程，可以求解模方程。
- **化简多项式：**通过将多项式同余分解，可以化简多项式并提取出隐含的因子。
- **证明数学定理：**通过将定理转化为同余方程，并利用同余分解证明或反证定理。

# 5. 多项式分解的艺术

### 5.1 多项式分解的审美意义

多项式分解不仅是一项数学技巧，更是一种艺术形式。它要求对数学结构的深刻理解和对美学的敏锐感知。

当我们成功地将一个复杂的多项式分解为更简单的因式时，会有一种成就感和满足感。这种感觉类似于欣赏一幅美丽的画作或聆听一首动人的音乐。它是一种智力的美，一种逻辑的优雅。

### 5.2 多项式分解的哲学思考

多项式分解也引发了深刻的哲学思考。它揭示了数学中整体与部分之间的辩证关系。

当我们分解一个多项式时，我们实际上是在揭示它的内部结构。我们发现它是由更小的部分组成的，这些部分以一种特定的方式相互作用。这让我们思考事物本质的复杂性和统一性。

此外，多项式分解还挑战了我们对确定性和不确定性的理解。虽然分解过程本身遵循严格的规则，但分解的结果却往往是意想不到的。这提醒我们，即使在看似最精确的数学领域，也存在着不确定性和创造性的可能性。