【布隆过滤器实用课】：大数据去重问题的终极解决方案

# 1. 布隆过滤器简介

## 1.1 布隆过滤器的概念

布隆过滤器（Bloom Filter）是一种空间效率极高的概率型数据结构，由Bloom在1970年提出，用于判断一个元素是否在一个集合中。它的核心优势在于在极低的误判率（假阳性率）情况下，使用远少于传统数据结构的存储空间，但其最主要的缺点是不能删除已经加入的元素。

## 1.2 布隆过滤器的应用场景

由于其空间效率，布隆过滤器广泛应用于网络服务、数据库系统、缓存机制等多种场景。例如，在分布式系统中，布隆过滤器可用于快速判断某个数据是否被缓存或者已经被处理过，从而避免重复的工作和不必要的网络通信。

## 1.3 布隆过滤器的原理简述

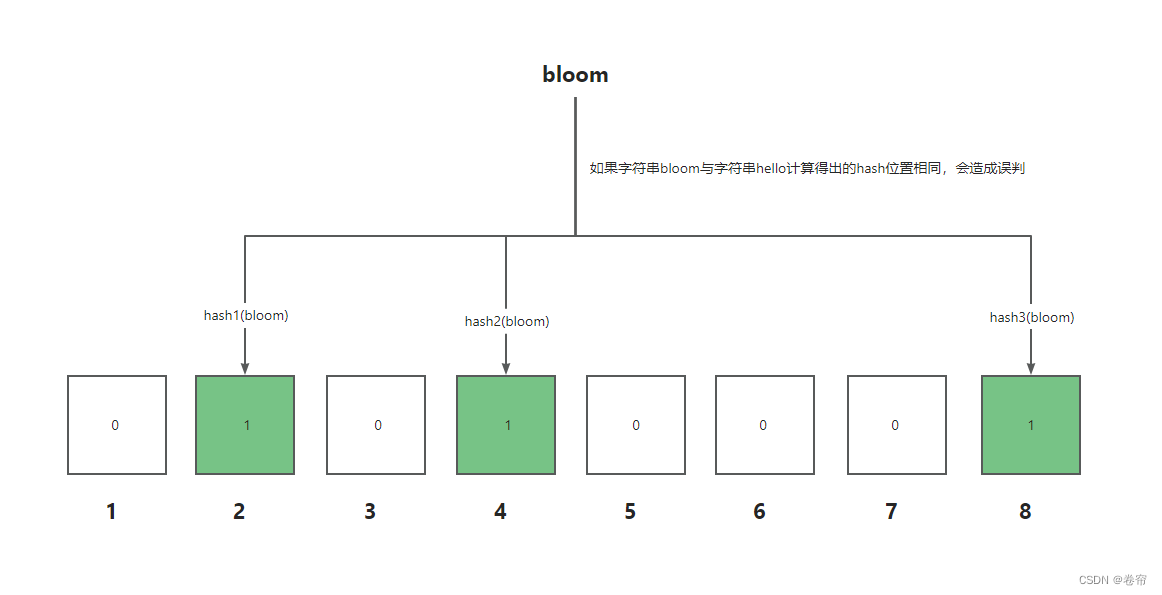
布隆过滤器的原理基于哈希函数和位数组。一个元素通过一组哈希函数被映射到位数组的一个位置，并将这些位置上的位标记为1。对于检查一个元素是否在集合中，只需看这些元素映射的位是否全部为1，即可判定元素是否存在。

+-----------------+
|     布隆过滤器   |
+-----------------+
|   位数组（bit）  |------> ***...
+-----------------+
|   哈希函数列表  |------> h1, h2, ..., hn
+-----------------+

要真正理解和应用布隆过滤器，接下来的章节我们将深入探讨它的理论基础、数学模型以及实现细节。

# 2. 理论基础与概率模型

在我们深入探讨布隆过滤器的实现和优化之前，理解其理论基础和概率模型是至关重要的。本章节将引导读者深入布隆过滤器的核心设计，揭开它的神秘面纱，包括其原理、数学模型、以及理论与实际应用之间的差距。

## 2.1 布隆过滤器的原理

### 2.1.1 基本概念和结构

布隆过滤器是一种空间效率极高的概率型数据结构，用于判断一个元素是否在一个集合中。它由伯顿·布隆于1970年提出。布隆过滤器的基本思想是在有限的空间内，通过k个独立的哈希函数将元素映射到位数组中，从而判断该元素是否在集合内。

在布隆过滤器的结构中，位数组是核心，所有操作都是围绕这个数组进行。当我们尝试添加一个元素时，我们会通过这k个哈希函数获取k个位置，并将这些位置对应位数组中的位设置为1。判断元素是否在集合内时，我们同样利用这k个哈希函数获取k个位置，检查所有这些位置的位是否都为1。如果有一个位不为1，则可以肯定元素不在集合内。

### 2.1.2 概率推导和参数选择

布隆过滤器的性能由假阳性率（false positive rate）和哈希函数数量k以及位数组的大小m决定。假阳性率定义为未插入的元素被错误地判断为已插入的概率。随着插入元素数量n的增加，假阳性率也会增加。

通过概率论推导，我们可以获得一组优化参数的近似解，以达到给定的假阳性率。位数组的大小m和哈希函数数量k可以通过以下公式估算：
\[ m = \left(\frac{-n \cdot \ln(p)}{(\ln(2))^2}\right) \]
\[ k = \frac{m}{n} \cdot \ln(2) \]
其中，p是目标假阳性率，n是要插入的元素数量。这些公式为我们提供了一个良好的起点来选择合适的m和k，以满足特定应用场景的需求。

## 2.2 布隆过滤器的数学模型

### 2.2.1 假阳性率分析

假阳性率是衡量布隆过滤器性能的关键指标。在没有任何插入操作时，假阳性率为0。随着插入操作的进行，假阳性率逐步增加。可以证明，对于给定的m和k，布隆过滤器的假阳性率随着插入元素数的增加而增加，呈指数级增长。

从数学角度分析，假阳性率p可以表示为：
\[ p \approx \left(1 - e^{-kn/m}\right)^k \]
该公式说明，当k和m固定时，假阳性率随着n的增加而增加，但增加的速度会随n的增大而减缓。该公式也表明，优化k和m的选择对于控制假阳性率至关重要。

### 2.2.2 过滤器大小和哈希函数数量的确定

在实际应用中，我们需要根据预期的元素数量、假阳性率容忍度来确定m和k的值。过大或过小的m和k都会对性能产生影响。如果m太大，空间浪费；如果m太小，假阳性率会过高。如果k太小，假阳性率同样会增加；如果k太大，每个元素的插入和查询操作会耗费更多时间。

一般情况下，我们会根据目标假阳性率p，通过上述公式计算出m和k。在实际应用中，还需要考虑到可能的负载因子变化，即实际插入元素数n可能与预期的不一致。因此，实际设计时可能会预留一定的余量，以适应未来可能的扩展需求。

## 2.3 理论与实际应用的差距

### 2.3.1 理论模型的局限性

理论模型在构建布隆过滤器时提供了宝贵的指导，但是它也有局限性。例如，模型假设哈希函数是完全随机且均匀分布的，这在实际中很难完全满足。真实的哈希函数可能会有冲突，且分布不均，这会导致实际的假阳性率高于理论推导的结果。

此外，模型没有考虑到实际操作过程中可能出现的错误，例如，当位数组非常大时，位数组的读写可能会出现延迟，以及在硬件层面可能出现的位翻转等问题。因此，实际应用中需要综合考虑这些因素，并进行适当的调整和优化。

### 2.3.2 实际应用中参数调整的策略

在实际应用中，参数调整策略是保证布隆过滤器性能的关键。一种常见的策略是动态调整哈希函数的数量k和位数组的大小m。当假阳性率超过预定阈值时，可以增加m的值，并重新选择k，以降低假阳性率。

另一种策略是使用多个布隆过滤器来分摊风险，比如采用多级布隆过滤器。每个过滤器使用不同的k和m，根据元素的特征或类型分别进行操作。这种方法不仅可以减少假阳性率，还可以增加布隆过滤器的灵活性，适应不同类型的数据处理需求。

此外，还可以针对具体应用场景进行优化。例如，在内存资源有限的情况下，可能需要设计一个能适应不同大小数据集的压缩型布隆过滤器，或者使用持久化存储来应对大规模数据集。实际应用中，需要根据具体情况权衡空间效率和时间效率，合理选择和调整参数。

以上就是第二章的内容，它为我们理解布隆过滤器的理论基础和概率模型提供了重要的视角，为接下来的实现和优化工作打下了坚实的基础。

# 3. 布隆过滤器的实现

## 3.1 硬件实现和软件实现的对比

### 3.1.1 硬件加速的优势与挑战

硬件加速通常涉及专门的计算设备，例如FPGA（现场可编程门阵列）或ASIC（应用特定集成电路）。这些硬件解决方案可以在执行重复和简单的数学运算时提供极高的效率。在布隆过滤器的上下文中，硬件实现通常意味着更快的哈希计算和位数组操作。因此，对于需要大量快速查询和插入操作的应用场景，硬件加速可以提供显著的性能提升。

尽管硬件加速提供了出色的性能，但它也存在一些挑战。首先是成本问题。研发和部署FPGA或ASIC解决方案的初始投资较高。其次，灵活性较差。与软件实现相比，硬件解决方案更难以修改和更新。此外，优化硬件设计通常需要在物理层面上进行调整，这需要深厚的电子工程知识。

### 3.1.2 软件实现的灵活性与效率

软件实现布隆过滤器的明显优势在于其灵活性。使用通用编程语言（如C++、Java或Python）可以快速开发和测试布隆过滤器。软件实现可以通过简单的代码更新来调整算法，或者根据需要更换哈希函数。而且，软件实现的开发和部署成本较低，更容易集成到现有系统中。

然而，软件实现的效率通常低于硬件实现。尤其是在需要处理极高吞吐量或极低延迟的应用时，软件处理速度可能会成为瓶颈。尽管如此，现代编程语言和编译器的优化技术（如JIT即时编译）已大幅提高了软件实现的性能，使得在许多情况下软件解决方案已经足够高效。

## 3.2 编程语言的选择与实现

### 3.2.1 各种编程语言实现的优缺点

不同编程语言在实现布隆过滤器时有着各自的优势和局限性。例如，C++因为其接近硬件的性能和灵活的内存管理，是实现高性能布隆过滤器的一个很好的选择。Java提供了跨平台的一致性和内置的垃圾收集机制，但可能会因为自动内存管理而带来性能开销。Python因其简单易用和丰富的库支持而受到开发者的喜爱，但其在性能上不如C++和Java。

### 3.2.2 关键代码解析与性能测试

关键代码实现布隆过滤器的基本操作，包括添加元素、检查元素是否存在以及初始化位数组。以下是使用Python实现的一个简单布隆过滤器示例代码：

import math
import mmh3
from bitarray import bitarray

class BloomFilter:
    def __init__(self, items_count, fp_prob):
        # items_count: 预计插入的元素总数
        # fp_prob: 允许的假阳性率
        self.fp_prob = fp_prob
        self.size = self.get_size(items_count, fp_prob)
        self.hash_count = self.get_hash_count(self.size, items_count)
        self.bit_array = bitarray(self.size)
        self.bit_array.setall(0)

    def add(self, item):
        # 使用多个哈希函数计算索引并设置位
        for i in range(self.hash_count):
            index = mmh3.hash(item, i) % self.size
            self.bit_array[index] = True

    def check(self, item):
        # 检查每个索引位置是否为True
        fo