WordCount在MapReduce中的应用：深入理解分片机制与优化

# 1. WordCount简介及基本原理

在大数据处理领域中，**WordCount**是一个经典的入门级案例，它实现了对一段文本中单词出现频率的统计。该程序不仅简单易懂，而且在学习分布式计算时提供了基础且直观的了解。

## 1.1 WordCount的基本原理

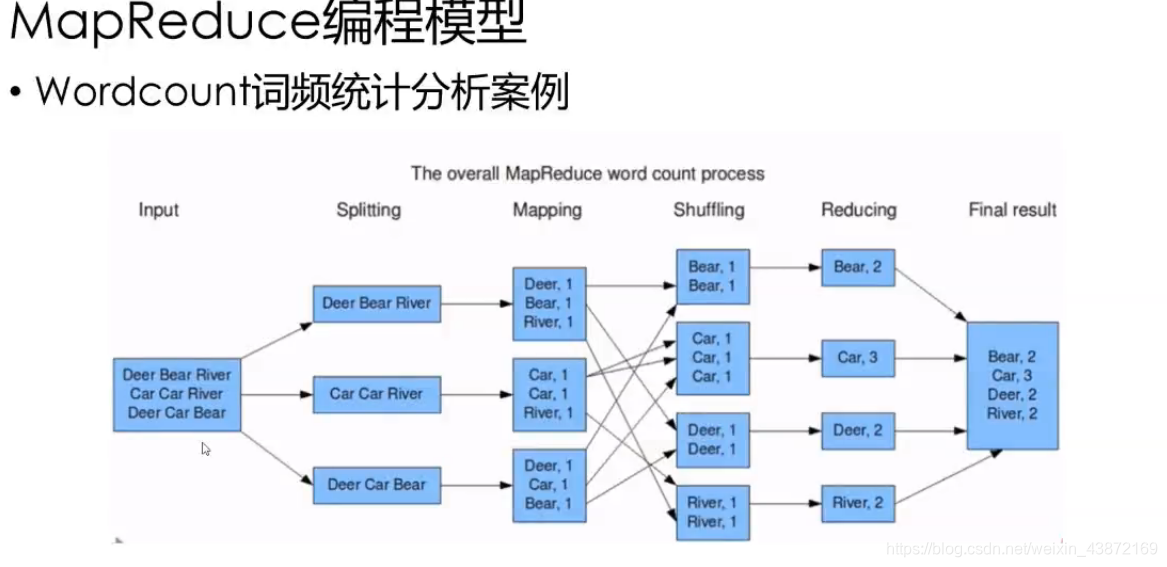
WordCount程序的工作原理可以概括为以下三个步骤：

1. **分割（Splitting）**：将输入数据分割成小数据块（称为分片），每个分片包含一部分文本数据。
2. **映射（Mapping）**：对每个分片中的文本进行处理，统计其中每个单词出现的次数，生成一系列键值对（word, count）。
3. **归约（Reducing）**：对所有映射产生的键值对进行合并操作，以汇总每个单词在整个数据集中的总出现次数。

这个过程涉及到的数据结构包括：键值对（key-value pairs），映射表（mappings）和归约操作（reductions）。WordCount的这种模式非常适合MapReduce编程模型，MapReduce模型由Google提出，并由Apache Hadoop框架广泛实现。

通过下一章我们将深入理解MapReduce的核心概念和分片机制，这将帮助我们更好地了解WordCount程序背后的原理及其在大数据处理中的重要性。

# 2. MapReduce核心概念与分片机制

### 2.1 MapReduce框架的组件与工作流程

MapReduce是一个编程模型，用于大规模数据集的并行运算。它的核心思想是“分而治之”，将大数据集切分成许多小数据集，由集群中的多个节点分别处理。

#### 2.1.1 输入分片与数据本地性

MapReduce将输入数据切分成固定大小的分片（split），每个分片作为独立的任务进行处理。数据本地性原则是MapReduce框架的重要优化策略，意在尽量在存储数据的物理机器上执行Map任务。

在Hadoop中，一个典型的输入分片大小是HDFS块的大小，通常是64MB或128MB。如果一个任务的输入数据位于同一HDFS块上，则这个任务就会尽量被调度到这个块所在的物理节点。

// 伪代码演示如何设置Hadoop的分片大小
Configuration conf = new Configuration();
// 设置分片大小为128MB
conf.set("mapreduce.input.fileinputformat.split.maxsize", "***");

#### 2.1.2 Map任务的处理

Map任务读取输入分片，处理数据并生成键值对（key-value pairs）。Map任务的输出会作为中间结果存储到磁盘上，并进行分区。

对于WordCount程序，Map函数会读取文本行，然后发出形如`(word, 1)`的键值对，表示单词及其出现的次数。

// Map函数示例
public static class TokenizerMapper
       extends Mapper<Object, Text, Text, IntWritable> {

    private final static IntWritable one = new IntWritable(1);
    private Text word = new Text();

    public void map(Object key, Text value, Context context
                    ) throws IOException, InterruptedException {
      // 将文本行分割成单词，并发出键值对
      StringTokenizer itr = new StringTokenizer(value.toString());
      while (itr.hasMoreTokens()) {
        word.set(itr.nextToken());
        context.write(word, one);
      }
    }
}

#### 2.1.3 Shuffle阶段的细节与优化

Shuffle阶段是MapReduce的核心部分，它负责将Map输出的中间数据进行排序、分区，并传输到Reduce任务所在的节点。

优化Shuffle阶段通常涉及调整中间数据的存储策略和网络传输优化。例如，使用Combiner在Map侧进行局部聚合可以减少Shuffle数据量。

// Combiner使用示例
job.setCombinerClass(MyCombiner.class);

### 2.2 分片机制详解

#### 2.2.1 默认分片策略与参数配置

Hadoop MapReduce的默认分片策略基于输入分片的大小。可以通过配置文件或代码中的参数来调整分片策略。

例如，可以通过以下配置来控制任务的并行度：

// 配置Map任务数量
job.setNumMapTasks(10);
// 配置Reduce任务数量
job.setNumReduceTasks(5);

#### 2.2.2 自定义分片器的实现与应用

在某些情况下，可能需要自定义分片器以更好地控制数据如何被分片。自定义分片器需要实现`org.apache.hadoop.mapreduce.Partitioner`接口。

// 自定义分片器的简单示例
public class CustomPartitioner extends Partitioner<Text, IntWritable> {
    public int getPartition(Text key, IntWritable value,
                            int numPartitions) {
        // 返回key的哈希值与numPartitions的模
        return (key.hashCode() & Integer.MAX_VALUE) % numPartitions;
    }
}

#### 2.2.3 分片与任务调度的关联

分片与任务调度紧密相关，好的分片策略可以提升任务的执行效率，减少数据传输开销。Map任务优先在拥有分片数据的节点上执行。

任务调度通常依赖于资源管理器（如YARN），它负责监控集群资源并调度任务。

下面是一个Mermaid流程图，描述了MapReduce工作流程：

graph LR
A[开始] --> B[输入分片]
B --> C[Map任务执行]
C --> D[Shuffle]
D --> E[Reduce任务执行]
E --> F[输出结果]

通过以上的介绍，我们可以看到MapReduce框架的工作流程，并且针对其中的分片机制进行了详细的解析。分片机制是MapReduce高效运行的关键，了解并应用好分片策略对于优化大数据处理至关重要。接下来的章节将继续深入介绍MapReduce在WordCount中的实现细节。

# 3. WordCount的MapReduce实现

MapReduce编程模型在大数据处理领域中占据着核心地位，而WordCount作为该模型的一个经典应用案例，是学习MapReduce的最佳起点。在本章中，我们将深入探讨WordCount在MapReduce框架下的实现方式，以及其背后的原理。通过分析关键代码，读者能够掌握Map和Reduce两个阶段的工作原理，并了解如何通过MapReduce框架实现一个完整的WordCount程序。

## 3.1 Map阶段的代码实现与原理分析

### 3.1.1 Map函数的工作流程

Map阶段的任务是处理输入数据，并将其转换为中间键值对（key-value pairs）。在WordCount案例中，Map函数读取原始文本数据，然后生成单词计数的中间键值对。每一个键值对中，键是单词本身，值是数字1，表示该单词出现了一次。

Map函数处理流程如下：

1. 输入数据被读取为一系列的记录，每条记录是一个键值对。
2. 对于每条记录，Map函数会对其值进行处理。
3. 处理的结果是一系列的中间键值对，这些键值对被写入到输出中。

### 3.1.2 关键代码解析

MapReduce编程中，开发者通常只需要关注Map函数和Reduce函数的实现。下面是一个简单的Map函数实现示例：

public static class TokenizerMapper
       extends Mapper<Object, Text, Text, IntWritable> {

    private final static IntWritable one = new IntWritable(1);
    private Text word = new Text();

    public void map(Object key, Text value, Context context
                    ) throws IOException, InterruptedException {
        StringTokenizer itr = new StringTokenizer(value.toString());
        while (itr.hasMoreTokens()) {
            word.set(itr.nextToken());
            context.write(word, one);
        }
    }
}

这段代码中，`TokenizerMapper`类继承自`Mapper`类。`map`方法是关键所在，它接受三个参数：

1. `Object key`：输入数据的键（在这里并不重要，因此使用Object类型）。
2. `Text value`：输入数据的值（在这里是文本数据）。
3. `Context context`：用于输出中间键值对的上下文。

方法体中使用`StringTokenizer`对输入的文本进行分词处理，并将每个单词作为键，数字1作为值输出。

### 3.1.3 实践操作

为了更好地理解Map函数的工作原理，我们可以通过以下几个步骤进行实践操作：

1. 安装并配置好Hadoop环境。
2. 编写上述J