聚类结果评估：量化聚类质量的专业方法论

# 1. 聚类分析基础概念

在探索数据的内在结构时，聚类分析是一种无监督的机器学习方法，用于将数据集中的样本划分为若干个由相似对象组成的群组或"簇"。这种技术在数据挖掘、市场细分、社交网络分析、图像分割等领域都有广泛应用。

## 1.1 聚类的目的与应用

聚类的目的是发现数据中的模式或集群，这些模式在很多情况下并不是显而易见的。在商业领域，聚类可以帮助企业识别不同的消费者群体；在生物学中，它可用于分类不同的植物或动物群体。

## 1.2 聚类分析的基本类型

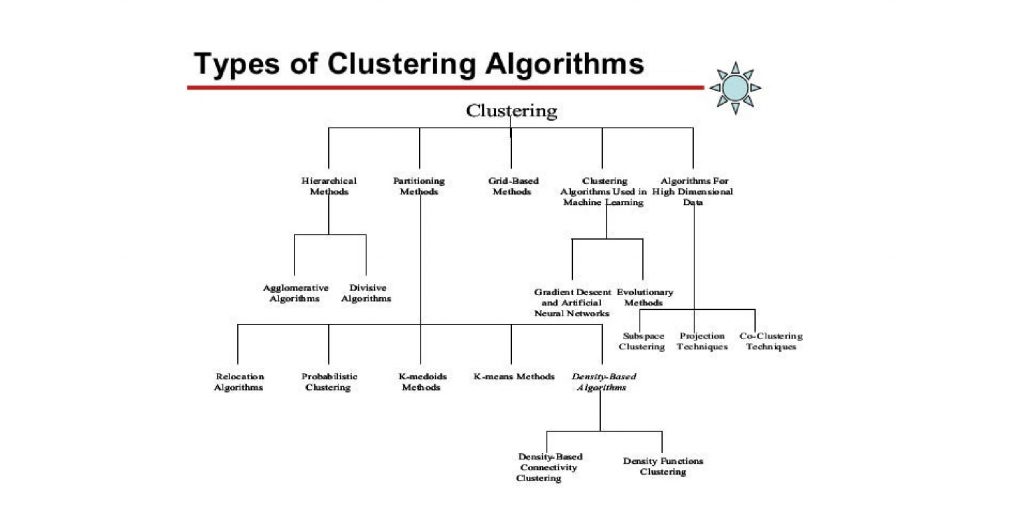
聚类可以基于不同的原则进行分类，常见的类型包括划分聚类（如K-means）、层次聚类（如凝聚与分裂法）、密度聚类（如DBSCAN）和基于模型的聚类。每种类型具有其独特的算法和适用场景，理解这些基本类型是深入学习聚类分析的前提。

聚类分析虽然方法多样，但核心思想在于如何衡量和比较对象之间的相似性，以及如何高效地组织这些对象以形成结构化的簇。为了达到这一目的，我们需要掌握一些基础的统计和机器学习知识，并且对所应用领域有所了解。只有这样，我们才能在实际问题中灵活运用聚类技术，发挥其强大的数据洞察力。

# 2. 评估聚类结果的理论方法

聚类是一种无监督学习技术，用于将数据集中的对象分组为相似的集合，称为簇。聚类分析的最终目标是创建有助于理解数据内在结构的簇。然而，聚类分析的一个主要挑战是评估聚类结果的质量。没有明确的目标簇可供比较，因此我们必须依赖内部和外部指标，以及稳定性分析，来确定聚类解决方案的有效性。

## 2.1 聚类评估的内部指标

内部指标利用数据集的内部信息来评估聚类结果。它们不依赖于外部信息，如真实标签，因此可以独立于任何真实类别信息进行评估。

### 2.1.1 轮廓系数

轮廓系数（Silhouette Coefficient）是一个衡量聚类质量的指标，其范围在 -1 到 +1 之间。轮廓系数接近 +1 表示样本离其自己的簇更接近，而离其他簇更远。轮廓系数计算公式如下：

\[ s(i) = \frac{b(i) - a(i)}{\max\{a(i), b(i)\}} \]

其中，\(s(i)\) 是样本 \(i\) 的轮廓系数，\(a(i)\) 是样本 \(i\) 到同簇样本的平均距离，而 \(b(i)\) 是样本 \(i\) 到最近簇的平均距离。

一个高轮廓系数表明簇内的样本很紧凑，而簇间的距离很远。

from sklearn.metrics import silhouette_score

# 假设 X 是数据集，labels 是聚类结果的标签
score = silhouette_score(X, labels)
print(f"轮廓系数: {score}")

### 2.1.2 戴维森堡丁指数

戴维森堡丁指数（Davies-Bouldin Index, DBI）是一个内部评估指标，用于衡量聚类结果的质量。该指标定义为聚类内相似度与聚类间差异的比值，其值越小，表示聚类效果越好。

\[ DBI = \frac{1}{k}\sum_{i=1}^{k} \max_{j \neq i} \left( \frac{\sigma_i + \sigma_j}{d(c_i, c_j)} \right) \]

其中，\(k\) 是簇的数量，\(\sigma_i\) 是第 \(i\) 个簇的标准差，\(c_i\) 是第 \(i\) 个簇的中心，\(d\) 是簇中心之间的距离。

DBI值越小表示聚类越理想。

from sklearn.metrics import davies_bouldin_score

# 假设 X 是数据集，labels 是聚类结果的标签
db_score = davies_bouldin_score(X, labels)
print(f"戴维森堡丁指数: {db_score}")

## 2.2 聚类评估的外部指标

外部指标将聚类结果与预先定义的“真实”标签进行比较，这些标签通常由专家人工标注。外部指标提供了一个衡量聚类效果的客观标准。

### 2.2.1 调整兰德指数

调整兰德指数（Adjusted Rand Index, ARI）衡量了聚类结果与真实标签之间的相似性。ARI的值范围是0到1，1表示完美匹配。

\[ ARI = \frac{\sum_{ij} \binom{n_{ij}}{2} - [\sum_i \binom{a_i}{2} \sum_j \binom{b_j}{2}] / \binom{n}{2}}{\frac{1}{2} [\sum_i \binom{a_i}{2} + \sum_j \binom{b_j}{2}] - [\sum_i \binom{a_i}{2} \sum_j \binom{b_j}{2}] / \binom{n}{2}} \]

其中，\(n_{ij}\) 是在第 \(i\) 个聚类簇和第 \(j\) 个真实标签簇中的共同样本数，\(a_i\) 和 \(b_j\) 分别是聚类簇 \(i\) 和真实标签簇 \(j\) 中的样本数，\(n\) 是样本总数。

from sklearn.metrics import adjusted_rand_score

# 假设 X 是数据集，labels 是聚类结果的标签，true_labels 是真实的标签
ari_score = adjusted_rand_score(labels, true_labels)
print(f"调整兰德指数: {ari_score}")

### 2.2.2 同质性、完整性和V-measure

同质性（Homogeneity）和完整性（Completeness）是衡量聚类结果与真实标签一致性的两个指标。同质性度量每个簇是否只包含一个类别的样本，完整性度量每个类别是否分配到一个簇中。

V-measure是同质性和完整性的调和平均数，定义如下：

\[ V = \frac{(1 + \beta) \times \text{Homogeneity} \times \text{Completeness}}{(\beta \times \text{Homogeneity}) + \text{Completeness}} \]

其中，\(\beta\) 是同质性和完整性的权重，通常设为1。

from sklearn.metrics import homogeneity_completeness_v_measure

# 假设 X 是数据集，labels 是聚类结果的标签，true_labels 是真实的标签
homogeneity, completeness, v_measure = homogeneity_completeness_v_measure(labels, true_labels)
print(f"同质性: {homogeneity}")
print(f"完整性: {completeness}")
print(f"V-measure: {v_measure}")

## 2.3 聚类评估的稳定性分析

稳定性分析是通过改变数据集的一些参数，例如对数据集进行重采样，来评估聚类结果的一致性。

### 2.3.1 重采样技术

聚类算法的稳定性可以通过重采样技术来评估。在重采样方法中，原始数据集被随机地划分成多个子集，然后对每个子集独立运行相同的聚类算法。然后，通过比较不同聚类结果的相似性，可以确定聚类算法的稳定程度。

### 2.3.2 稳定性指标的选择和计算

一个常见的稳定性指标是Jaccard指数。Jaccard指数是度量两个样本集的相似度的统计量。定义如下：

\[ J(A, B) = \frac{|A \cap B|}{|A \cup B|} \]

其中，\(A\) 和 \(B\) 是两个不同聚类运行的簇集合。Jaccard指数值越接近1，表示聚类结果越稳定。

from sklearn.metrics import jaccard_score

# 假设 cluster_labels_1 和 cluster_labels_2 是两组不同的聚类结果标签
jaccard = jaccard_score(cluster_labels_1, cluster_labels_2)
print(f"Jaccard指数: {jaccard}")

通过内部指标、外部指标和稳定性分析，可以综合评估聚类结果的质量。这些方法相互补充，为我们提供了全面评价聚类效果的工具。

聚类评估方法的高级应用中，将介绍大数据环境下的聚类评估以及在特定领域的应用，让我们深入理解如何将这些评估方法应用于复杂和大规模的数据集。在大数据环境下，聚类评估面临新的挑战，如计算效率和算法的扩展性。特定领域的应用展示了聚类评估方法如何帮助我们在诸如生物信息学和社交网络分析等特定场景中提取有价值的洞察。

# 3. 可视化技术在聚类评估中的应用

聚类分析的结果需要通过直观的方式来展示，以便更好地理解数据的分布和聚类的结构。可视化技术是数据科学和机器学习中不可或缺的部分，它在聚类评估中扮演着重要的