递归算法在流行病学中的应用：【从SIR模型到现实案例】的演进路径


参考资源链接：[递归算法求解传染病问题](https://wenku.csdn.net/doc/6412b75bbe7fbd1778d4a00d?spm=1055.2635.3001.10343)
# 1. 递归算法与流行病学基础

在流行病学的研究中，递归算法作为一种重要的数学工具，起着至关重要的作用。通过递归，我们可以模拟疾病的传播过程，从而帮助我们更好地理解疾病的发展趋势和影响因素。递归算法的基本思想是将复杂的问题分解为简单的子问题，通过解决这些子问题来解决整个问题。

## 1.1 递归算法简介
递归算法是一种通过函数自我调用来解决问题的算法。在流行病学中，我们可以利用递归算法来模拟疾病的传播过程，通过设定初始的感染人数，以及每次传播的感染率，就可以通过递归算法来预测疾病的传播趋势。

## 1.2 流行病学基础
流行病学是研究疾病的分布、决定因素以及如何控制和预防疾病的科学。在流行病学中，我们通常会使用数学模型来描述疾病的传播过程，而递归算法正是实现这些模型的重要工具。

## 1.3 递归算法与流行病学的结合
将递归算法应用于流行病学，可以帮助我们更好地理解和预测疾病的传播过程。例如，在SIR模型中，我们可以通过递归算法来计算每个时间点的易感染人数、感染人数和康复人数，从而预测疾病的传播趋势。

# 2. SIR模型的理论与实现

## 2.1 SIR模型的数学基础
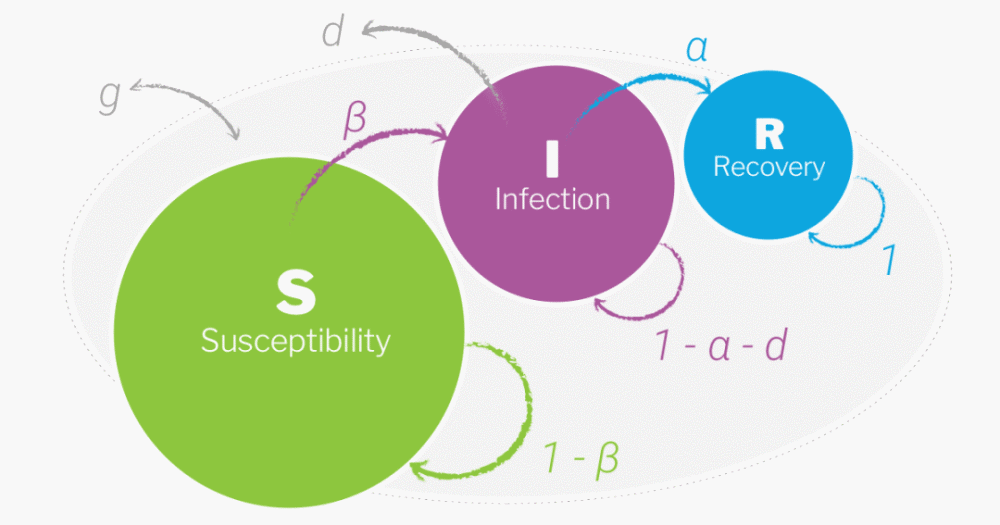
在流行病学中，模型是用来描述传染病传播动态的重要工具。SIR模型是最简单的流行病学模型之一，它通过微分方程来模拟易感者(Susceptible)、感染者(Infectious)和移除者(Removed)三类人群的数量变化。

### 2.1.1 微分方程在流行病学中的应用
微分方程在流行病学中用于描述随时间变化的传染病传播过程。SIR模型中的微分方程组如下：

\[
\begin{cases}
\frac{dS}{dt} = -\beta \frac{SI}{N}, \\
\frac{dI}{dt} = \beta \frac{SI}{N} - \gamma I, \\
\frac{dR}{dt} = \gamma I.
\end{cases}
\]

其中，\(S(t)\)、\(I(t)\)和\(R(t)\)分别代表时间\(t\)时刻易感者、感染者和移除者的数量，\(N\)是总人口数，\(\beta\)是感染率，而\(\gamma\)是恢复率。

### 2.1.2 SIR模型的构建与假设
SIR模型假设人群是封闭的，即没有出生或死亡，也没有迁移；所有个体在感染后都会成为易感者；一旦感染，个体将具有相同的潜伏期和传染期，且在传染期结束后将移除出模型。

## 2.2 SIR模型的递归表达
递归函数通过定义在更小规模的相似问题上的解来构建问题的解。在SIR模型中，递归表达可以用来推导每一时刻的\(S\)、\(I\)、\(R\)。

### 2.2.1 递归函数在模型中的角色
递归函数在SIR模型中的应用是通过计算时间步长\(\Delta t\)后的人群变化量来实现的。在离散时间下，SIR模型的递归公式如下：

\[
\begin{cases}
S_{t+\Delta t} = S_t - \beta \frac{S_t I_t}{N} \Delta t, \\
I_{t+\Delta t} = I_t + (\beta \frac{S_t I_t}{N} - \gamma I_t) \Delta t, \\
R_{t+\Delta t} = R_t + \gamma I_t \Delta t.
\end{cases}
\]

### 2.2.2 递归解与数值解的比较
递归解通常是通过递归函数在每一次迭代中的计算结果得到的，而数值解则通过求解微分方程组的数值方法，如欧拉方法或龙格-库塔方法获得。递归解的简单性适合于概念验证，但在长时期模拟时可能因累积误差导致较大的偏差。

## 2.3 SIR模型的参数估计与验证
为了使模型更贴近实际情况，需要对SIR模型的参数进行估计和验证。模型参数的识别和校准通常利用实际疫情数据。

### 2.3.1 参数识别方法
参数识别是指通过统计和优化方法来确定模型参数值的过程。一个常用的方法是使用最小二乘法，该方法寻找使模型预测与实际数据差异最小的参数值。

### 2.3.2 模型与真实数据的匹配
通过历史数据来校准模型，可以更准确地预测未来的疫情趋势。模型的评估通常通过对比模型预测值和实际数据的契合程度来进行，使用的方法包括但不限于均方误差(MSE)和决定系数(R²)等统计指标。

在这一章中，我们将深入探讨SIR模型的理论基础和实现细节，包括其数学建模、递归表达、以及模型参数的识别和校准方法。这些内容对于理解和应用SIR模型至关重要。接下来的章节将进一步探讨递归算法在流行病学模型中的实践应用。

# 3. 递归算法在流行病学中的实践应用

## 3.1 实时疫情数据的递归分析
### 3.1.1 数据获取与预处理

实时疫情数据的获取是分析的第一步，也是至关重要的一步。疫情数据来源于官方卫生组织、医疗机构以及各种健康监测系统的实时更新。获取数据后，需要进行预处理，以便于后续分析。预处理通常包括数据清洗、格式转换和缺失值处理等步骤。数据清洗指的是去除错误或不合理的数据记录，格式转换是指将数据转换为统一的格式，以方便后续处理，而缺失值处理可能涉及到数据的插值或估算。

代码块展示一个简单的数据预处理流程：

import pandas as pd
from sklearn.impute import SimpleImputer

# 假设df是原始数据的DataFrame
# 去除缺失值
df_cleaned = df.dropna()

# 或者填充缺失值，这里使用平均值填充
imputer = SimpleImputer(missing_values=np.nan, strategy='mean')
df_filled = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)

# 格式转换可以使用pandas的to_datetime函数
df['date'] = pd.to_datetime(df['date'])

# 数据存储
df_cleaned.to_csv('cleaned_data.csv', index=False)

数据分析的预处理逻辑应根据实际数据集的特性和需求进行调整。例如，对于时间序列数据，可能需要考虑时间序列的对齐和重新采样等问题。

### 3.1.2 递归算法在疫情趋势预测中的应用

递归算法在疫情趋势预测中的应用主要体现在其处理时间序列数据的能力上。利用递归算法，我们可以构建模型来预测未来的疫情发展。例如，可以使用递归神经网络（RNN）或长短期记忆网络（LSTM）来预测疫情的流行趋势。

LSTM模型特别适合处理和预测时间序列数据中的重要事件，因此在疫情趋势预测中得到了广泛应用。下面是一个使用Keras构建LSTM模型的代码示例：

from keras.models import Sequential
from keras.layers import LSTM, Dense

# 假设X_train和y_train是训练数据
model = Sequential()
model.add(LSTM(units=50, return_sequences=True, input_shape=(X_train.shape[1], 1)))
model.add(LSTM(units=50, return_sequences=False))
model.add(Dense(units=1))

model.c