深度解析：【递归算法】如何成为传染病解决方案的关键武器


参考资源链接：[递归算法求解传染病问题](https://wenku.csdn.net/doc/6412b75bbe7fbd1778d4a00d?spm=1055.2635.3001.10343)
# 1. 递归算法的理论基础与传染病学概述

在信息时代，递归算法作为一种重要的编程技巧，已成为解决问题的关键工具。在这一章中，我们将深入探讨递归算法的理论基础，并将其与传染病学这一应用领域相结合，为理解后续章节的算法应用打下坚实的基础。

## 1.1 递归算法的理论基础
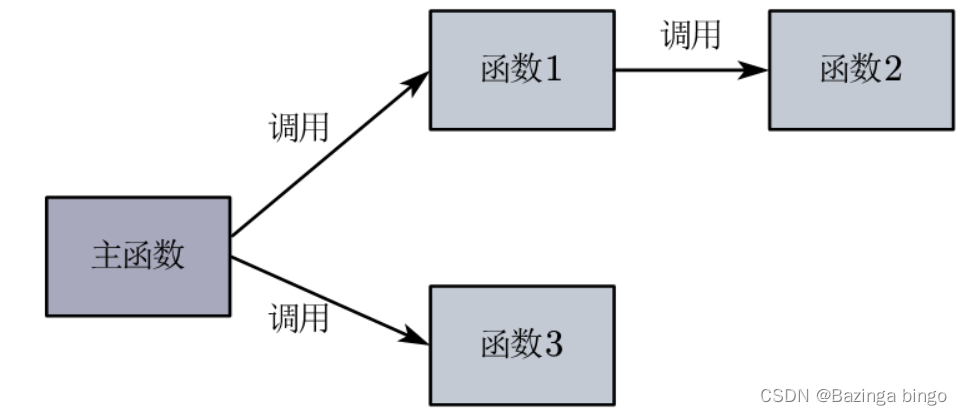
递归算法，顾名思义，是一种通过函数调用自身来解决问题的方法。它由两个主要部分组成：基本情况和递归情况。在基本情况中，算法可以得出简单问题的直接答案；而在递归情况中，算法将问题分解为更小的子问题，直至可以应用基本情况。

递归算法的关键在于能够不断地将问题规模缩小，并最终解决问题。但同时也需要特别注意递归深度和效率问题，因为过度的递归调用可能导致栈溢出或者过长的计算时间。

## 1.2 传染病学简介
传染病学是研究传染病及其防治的科学，其核心在于分析疾病的传播机制，以及如何有效地控制和预防这些疾病。在这一过程中，递归算法可以用来建立和解决传染病的数学模型，这对于理解疾病的传播过程、预测疾病趋势，以及制定有效的公共卫生策略至关重要。

在下一章，我们将详细探讨递归算法是如何在构建传染病传播模型中发挥作用的。通过结合递归算法和传染病学的具体案例，我们能够更清晰地理解这种算法在现实世界中的应用和价值。

# 2. 递归算法在传染病模型中的应用

## 2.1 递归算法原理与传染病传播的数学模型
### 2.1.1 递归的基本概念及其在数学建模中的作用

递归是一种在数学、逻辑学、计算机科学等领域广泛使用的编程方法，它允许一个过程或函数直接或间接地调用自身。递归的核心思想是将问题分解为更小的相似问题，直到达到一个简单直观的基准情况（base case）。

在数学建模中，递归方法有助于解决分形结构和动态过程的问题。比如在传染病学中，病毒传播的动态可以递归地表述为感染者与未感染者之间的接触过程。

#### 递归公式
递归算法通常用递归公式来定义，形式如下：

f(n) = g(f(n-1), f(n-2), ..., f(n-k))

其中`f(n)`是当前的函数值，`f(n-1), f(n-2), ..., f(n-k)`是先前的函数值，`g`是递归函数，它描述了如何从前`k`个值计算当前值。

#### 递归在数学建模中的角色
在传染病传播的数学模型中，递归可以用来描述连续时间的感染过程或离散时间的感染者数量变化。例如，SIR模型的递归版本可以用来预测未来某天的感染者数量，通过递归公式：

S(t+1) = S(t) - B * S(t) * I(t)
I(t+1) = I(t) + B * S(t) * I(t) - γ * I(t)

其中，`S(t)`和`I(t)`分别是时间`t`时刻的易感者和感染者数量，`B`是感染率，`γ`是康复率。

### 2.1.2 传染病传播模型的构建与递归表达

构建传染病传播模型，通常需要以下几个步骤：

1. 定义状态：将人群划分为易感者(Susceptible)、感染者(Infectious)和康复者(Recovered)，即SIR模型。
2. 建立方程：根据流行病学的实际情况，建立描述人群状态转移的微分方程或差分方程。
3. 参数估计：使用历史数据和统计方法对模型中的关键参数（如感染率、康复率）进行估计。
4. 递归实现：利用递归公式来模拟或预测传染病的传播过程。

#### 模型递归化

在递归化的过程中，需要考虑如何简化问题。例如，为了使模型适用于递归算法，可以将连续时间模型转化为离散时间模型。在离散时间模型中，我们通常将一个完整的传播周期划分为n个小的时间单位，在每个时间单位内应用递归公式进行计算。

#### 代码实现示例

以下是一个简单的SIR模型递归实现的代码块：

def sir_model(S, I, R, N, beta, gamma, days):
    results = []
    for day in range(days):
        new_infections = -beta * S * I / N
        new_recoveries = gamma * I
        S += new_infections
        I += new_infections - new_recoveries
        R += new_recoveries
        results.append((S, I, R))
    return results

**逻辑分析**：代码中定义了一个`sir_model`函数，它接受易感者(S)、感染者(I)、康复者(R)的人数，人群总数(N)，感染率(beta)、康复率(gamma)，以及模拟天数(days)作为输入参数。在每个时间单位，计算新感染人数和新康复人数，然后更新S、I和R的值，并将结果记录在列表`results`中返回。

**参数说明**：
- `S`, `I`, `R` 分别代表易感者、感染者和康复者的数量。
- `N` 是人群的总数。
- `beta` 是感染率，它定义了一个易感者成为感染者的概率。
- `gamma` 是康复率，它定义了一个感染者康复的概率。
- `days` 是模型运行的总天数。

接下来，我们需要讨论如何将这种递归模型应用于SIR模型，并探讨其实施方式。

# 3. 递归算法的实践应用与疫情控制策略

## 3.1 递归算法在疫情数据分析中的应用

### 3.1.1 数据收集与处理

在疫情数据分析中，递归算法可以帮助我们更好地理解和预测疫情的动态。首先，我们需要收集相关的疫情数据，包括但不限于确诊人数、治愈人数、死亡人数、新增病例数、病原体检测情况等。这些数据来源于各种公开的疫情报告、医疗健康机构、社交媒体、移动应用等。数据收集的目的是为了获得一个全面、多维度的疫情视图。

收集到的数据通常需要经过预处理才能用于递归模型的建立。数据预处理包括清洗、格式化、归一化等步骤。清洗是为了去除数据中的异常值和错误，确保数据质量；格式化是为了使数据符合模型输入的格式；归一化则是为了消除不同变量之间的量纲影响，使得模型能够公平地处理各种特征。递归算法在这一过程中可以被用于识别数据中的异常模式或趋势，进一步指导数据分析的方向。

### 3.1.2 递归算法辅助疫情趋势预测

递归算法在疫情数据分析中的第二个关键应用是辅助疫情趋势预测。通过递归模型的建立，我们可以分析疫情的时间序列数据，并预测未来一段时间内的病例发展趋势。递归模型特别适合处理这种随时间变化的数据，因为它能够利用历史信息来预测未来的状态。

举例来说，我们可以使用简单的递归函数来模拟每天的新增病例数。设 \( N(t) \) 为第 \( t \) 天的新增病例数，我们可以建立一个递归公式来描述 \( N(t) \) 的变化：

def predict_new_cases(days_to_forecast, today, cases_history):
    predictions = []
    for i in range(days_to_forecast):
        if i == 0:
            # 基于当前新增病例数和过去趋势进行预测
            new_case = cases_history[-1] + (cases_history[-1] - cases_history[-2])
        else:
            # 使用前一天的预测结果
            new_case = predictions[-1] + (predictions[-1] - predictions[-2])
        predictions.append(new_case)
    return predictions

在上述代码中，`days_to_forecast` 指的是我们想要预测的天数，`today` 表示今天的日期，而 `cases_history` 是一个包含过去N天新增病例数的列表。这个简单的模型基于连续两天新增病例数的变化趋势来预测未来每一天的新增病例数。当然，现实中的疫情模型要复杂得多，会涉及多个变量和更精细的数学公式。

通过分析递归模型的预测结果，决策者可以更好地制定应对策略，例如增加医疗资源、制定出行限制措施等。

## 3.2 递归算法在制定公共卫生干预措施中的角色

### 3.2.1 干预措施的选择与模拟

在制定公共卫生干预措施时，决策者需要评估不同措施对于控制疫情的有效性。递归算法可以用来模拟不同干预措施的可能结果。比如，我们可以建立一个模型来模拟限制社交活动对疫情传播速度的影响。

在这个模拟中，我们可能会考虑以下几个因素：

- 社交限制的程度（如限制集会的大小）
- 限制的持续时间
- 人群的遵守程度

使用递归模型，我们可以根据这些参数的变化来观察疫情传播的可能趋势。以下是一个简化的代码示例，展示如何使用递归模拟社交限制的效果：

def simulate_social_distancing(days, current_infections, distancing_level):
    infections = current_infections
    for day in range(days):
        # 根据社交限制程度计算传播因子
        transmission_rate = 1 - distancing_level
        new_infections = infections * transmission_rate
        infections += new_infections
    return infections

在这个模拟中，`days` 是模拟的天数，`current_infections` 是当前的感染人数，而 `distancing_level` 是一个介于0到1之间的值，表示社交限制的程度。传播因子（transmission_rate）会随着限制的增强而减小，进而减少新感染人数。通过递归地进行每天的模拟，我们可以评估出社交限制措施的长期效果。

### 3.2.2 递归算法评估干预效果

为了评估干预措施的效果，我们需要能够量化干预前后的变化。递归算法在这一环节中的作用是评估疫情的关键指标，如传播速度、感染率和病死率等，并预测在不同干预措施下这些指标的变化情况。

我们可以使用递归函数来构建一个预测模型，对每个关键指标进行跟踪和预测。例如，我们可以模拟不同的疫苗接种率对群体免疫的影响，或者评估增强个人防护措施的效果。

以下是一个递归函数的示例，用于模拟在不同疫苗接种率下的感染率变化：

def vaccine_effectiveness(days, susceptible_population, vaccination_rate):
    vaccinated_population = susceptible_population * vaccination_rate
    infection_rate = 1 / (1 + vaccinated_population * vaccine_protection)
    infections = susceptible_population * infection_rate
    return infections

在这个函数中，`days` 是模拟的天数，`susceptible_population` 是易感人群的数量，而 `vaccination_rate` 表示疫苗接种率。函数计算每天感染的预期人数，这里简化了模型，假设疫苗提供了一定程度的保护（`vaccine_protection`），并且所有人都有相同的感染风险。

通过这样的模拟，我们可以量化分析疫苗接种对减少感染和控制疫情的效果。递归算法在这一环节帮助我们理解和预测在不同公共卫生政策下疫情的可能走向，为决策者提供科学依据。

## 3.3 递归算法优化与疫情防控的实时调整

### 3.3.1 算法效率优化策略

随着疫情数据量的增大和模型复杂性的提升，优化递归算法的效率变得至关重要。优化递归算法不仅可以加快模型的运行速度，还可以提高模型的准确性和适应性。常见的递归算法优化策略包括使用记忆化（memoization）技术、避免重复计算以及减少递归深度等。

记忆化是通过存储已经计算过的中间结果来避免重复计算，尤其适用于结果具有重叠子问题的递归问题。例如，在计算斐波那契数列时，我们可以使用字典来存储已经计算过的值：

def fibonacci_memoization(n, memo={}):
    if n in memo:
        return memo[n]
    if n <= 2:
        return 1
    memo[n] = fibonacci_memoization(n - 1, memo) + fibonacci_memoization(n - 2, memo)
    return memo[n]

在这个优化后的斐波那契数列计算函数中，`memo` 字典用于存储已经计算过的值。当我们需要计算一个斐波那契数时，首先检查 `memo` 中是否已经存储了该值，如果已经存储，则直接返回该值，否则进行计算并存储结果。

在疫情模型中，我们可以使用类似的方法来存储和重用一些复杂的计算结果，例如人口分布、传播途径等参数的计算结果。通过减少计算量，我们提高了递归模型的效率，使其能够处理更大的数据集，更快速地响应疫情数据的更新。

### 3.3.2 面对新变种病毒的算法适应性调整

在疫情防控过程中，病毒的变异是造成预测困难的主要原因之一。病毒变种可能导致传播速度、传播方式、致病性的改变，这对疫情预测模型提出了新的挑战。因此，递归算法在疫情模型中需要具备一定的适应性调整能力，以适应新变种病毒的特性。

为了使模型适应新的变种病毒，我们需要重新评估和调整模型中的关键参数。例如，如果某个变种病毒的传染性增强，我们需要调整模型中的传播率参数。在递归模型中，这可能意味着改变递归函数的初始条件或者递归关系式。

def new_strain_simulation(days, initial_infections, transmission_rate, variant_adjustment):
    infections = initial_infections
    for day in range(days):
        new_infections = infections * transmission_rate * variant_adjustment
        infections += new_infections
    return infections

在上述代码中，`variant_adjustment` 是针对新变种病毒传播特性的一个调整因子。当出现新变种病毒时，我们根据实验室数据和流行病学研究来设定这个因子的值，然后使用递归模型来预测新变种病毒的传播情况。

此外，递归模型的适应性调整还需要依赖于实时的数据更新和模型参数的不断优化。随着对新变种病毒的了解增加，我们需要定期重新训练和调整模型，确保模型能够反映最新的疫情状况。递归算法的灵活性使其成为应对新变种病毒挑战的有效工具。

总结来说，在面对新变种病毒时，递归模型需要结合最新的疫情数据和科学研究结果，不断调整和优化模型参数，以确保模型的准确性和预测的可靠性。通过递归模型的持续调整和适应，我们能够更好地理解和预测疫情的发展，为公共卫生决策提供更科学的依据。

以上为第三章的详细内容，分别讨论了递归算法在疫情数据分析中的应用，如何利用递归算法制定公共卫生干预措施，以及如何进行递归算法的优化和对新变种病毒的适应性调整。这些内容旨在为IT行业从业者提供深入的分析和实际应用案例，展示递归算法在抗击疫情中的潜力和价值。

# 4. 递归算法在疫苗分配和群体免疫中的策略运用

疫苗分配和群体免疫是传染病控制策略中的关键环节。递归算法作为一种强有力的数学工具，能够在处理这类问题时提供独特的视角和解决方案。本章将深入探讨递归算法在优化疫苗分配策略、制定群体免疫策略以及在疫情长期管理中所发挥的作用。

## 4.1 疫苗分配模型与递归算法优化

### 4.1.1 疫苗分配问题的复杂性与递归解法

疫苗分配问题的复杂性主要源于需求的不确定性、资源的有限性以及分配过程中的时间因素。递归算法能够通过构建决策树来解决这类问题，每个决策节点都代表着在特定时间点的疫苗分配方案，而递归则用于探索这些决策点的所有可能情况。

#### 决策树构建示例

以一个简化的疫苗分配问题为例，假设某城市有3个区域（A、B、C），每个区域的居民数量不同，疫苗供应量有限，并且我们需要在不同时间段内做出分配决策。

时间T1
├── 区域A分配100剂
│   ├── 时间T2
│   │   ├── 区域B分配50剂
│   │   │   ├── 时间T3
│   │   │   │   ├── 区域C分配剩余全部疫苗
│   │   │   └── ...
│   │   └── ...
├── 区域B分配150剂
└── ...

递归解法将在每个时间点上评估不同的分配方案，并使用回溯法来撤销那些最终导致不理想结果的决策。

### 4.1.2 递归算法在优化疫苗分配中的实例分析

为了具体展示递归算法如何应用于疫苗分配问题，我们设计一个简单的模拟场景。假设有两个区域，每个区域都有100人需要接种疫苗，总共有150剂疫苗可供分配。我们希望最大化接种人数。

def maximize_vaccinations(region_a, region_b, total_vaccines):
    if region_a == 0 and region_b == 0:
        return total_vaccines
    if region_a == 0:
        return region_b
    if region_b == 0:
        return region_a
    if total_vaccines == 0:
        return min(region_a, region_b)
    # 尝试为区域A分配尽可能多的疫苗，然后为区域B分配剩余的
    max_vaccinated = max(
        maximize_vaccinations(region_a - 1, region_b, total_vaccines - 1),
        maximize_vaccinations(region_a, region_b - 1, total_vaccines - 1)
    )
    return max_vaccinated

# 假设两个区域的人数都是100
maximize_vaccinations(100, 100, 150)

该函数模拟了递归过程，尝试为每个区域分配疫苗，并计算接种人数的最大值。递归的终止条件是所有疫苗已分配完毕或者某个区域的人数已经减少到0。

通过执行这段代码，我们可以得出在有限的资源下，如何分配疫苗才能使得接种人数最大化。

## 4.2 群体免疫的递归模型与策略制定

### 4.2.1 群体免疫的基本理论

群体免疫是指当足够多的人口对某种传染病免疫时，疾病的传播将被显著减缓甚至停止。这个阈值称为群体免疫阈值，其大小取决于传染病的传染率。递归算法可以用来估计达到群体免疫所需的免疫率。

### 4.2.2 递归算法在群体免疫策略中的应用

递归算法通过模型模拟不同免疫接种率下的疫情传播，找到实现群体免疫的最小接种率。

def estimate_herd_immunity(population, infection_rate):
    threshold = 1 - (1 / infection_rate)
    vaccinated = 0
    while True:
        vaccinated += 1
        if vaccinated / population >= threshold:
            return vaccinated

# 假设人口总数为100000，传染病的传染率为3
estimate_herd_immunity(100000, 3)

上述代码模拟了递归过程，逐步增加免疫人口数，直到达到群体免疫阈值。通过这种计算，我们可以估计出在给定的传染率下，需要对多少人进行免疫接种才能实现群体免疫。

## 4.3 递归算法在疫情长期管理中的持续作用

### 4.3.1 疫情的长期监测与递归算法的周期性应用

为了应对疫情的长期影响，递归算法可以在疫情监测中周期性地应用，预测疫情的周期性波动，并提供相应的干预措施。

### 4.3.2 递归模型的动态更新与持续策略优化

随着疫情数据的更新，递归模型需要动态调整以反映最新的疫情发展情况。递归算法通过引入最新的疫情数据，对模型参数进行调整，从而持续优化疫情管理策略。

递归算法不仅提供了一个理论框架来理解疫情的发展和群体免疫的实现，而且通过实际的数据和模型，对疫情控制策略进行了深入的分析和优化。这种算法与实践相结合的方法，在未来对疫情控制仍将是不可或缺的一部分。

# 5. 递归算法在新兴传染病模型中的创新应用

递归算法作为数学建模和计算机科学中的一种重要技术，其在处理传染病模型方面的应用是多面的。新兴传染病的特点对现有的数学模型提出了新的挑战。本章节将探讨递归算法如何适应这些挑战，并为预测和应对新型传染病提供解决方案。

## 5.1 新兴传染病特征与递归模型的适应性

### 5.1.1 新兴传染病的特点与挑战

新兴传染病指的是新出现或重新出现的人类疾病，这些疾病由于多种原因，在人群中传播速度快，影响范围广。这类传染病的特点包括病原体的新颖性、传播途径的不确定性、人群易感性的广泛性等。例如，新型冠状病毒（SARS-CoV-2）引起的COVID-19就是近年来最典型的新兴传染病。

递归模型在处理这类问题时面临显著挑战，包括：

- 数据的不完整性：在疾病初期，对病原体的认识不足导致数据收集困难。
- 动态变化的传播机制：随着病原体变异，其传播方式可能发生变化，对模型预测产生影响。
- 多重因素的作用：社会、经济、环境等多种因素与疾病传播相互作用，增加了模型的复杂性。

### 5.1.2 递归模型的扩展与创新方法

为适应新兴传染病的特点，递归模型需要进行以下几方面的扩展和创新：

- **模块化设计**：将模型分解为可独立更新的模块，以应对数据不完整性和传播机制变化的挑战。
- **集成多元数据源**：结合实时数据和历史数据，利用大数据技术，增强模型的预测能力。
- **多尺度建模**：建立从小尺度（如社区、医院）到大尺度（如国家、全球）的传染病传播模型，以适应不同层面的干预措施。

## 5.2 递归算法在多因素影响下的传染病预测

### 5.2.1 多因素交互作用对疫情的影响分析

传染病的传播是一个复杂的动态系统，受多种因素的影响。这些因素包括：

- 人口流动性：人口的迁移和旅行会加速病毒的传播。
- 公共卫生措施：如疫苗接种率、隔离政策、戴口罩等都会影响疫情的发展。
- 社会行为：个人和群体的行为习惯，比如社交距离，对疫情有直接影响。

递归模型需要考虑到这些因素，通过引入相应的参数和反馈机制来模拟它们对疫情的综合影响。

### 5.2.2 递归算法在综合因素分析中的应用

递归算法在多因素传染病预测模型中的应用通常涉及以下方面：

- **因素权重调整**：根据实时数据动态调整各因素的权重。
- **条件递归**：在不同条件下切换模型的行为，以反映公共卫生政策和人群行为的改变。
- **敏感性分析**：进行敏感性分析来识别对疫情预测影响最大的关键因素。

def dynamic_weight_adjustment(data, weights):
    """
    动态调整因素权重的函数

    :param data: 包含多元数据源的数据集
    :param weights: 初始因素权重列表
    :return: 调整后权重列表
    """
    # 这里是模拟权重调整过程的伪代码
    updated_weights = []
    for weight in weights:
        # 假设使用某些统计方法根据新数据调整权重
        new_weight = adjust_weight_by_statistics(data, weight)
        updated_weights.append(new_weight)
    return updated_weights

# 参数解释：
# data: 包含疫情相关多元数据的数组，如人流数据、疫苗接种率等。
# weights: 各因素在模型中的初始权重。
# adjust_weight_by_statistics: 一个假设的函数，它根据最新的数据统计分析结果来调整权重。

# 请注意，上面的代码仅为示例，实际应用中需要根据具体情况进行编码实现。

## 5.3 递归算法的未来发展方向与疫情解决方案

### 5.3.1 递归算法的未来技术趋势

递归算法在预测新兴传染病方面的未来发展可能集中在以下趋势：

- **智能化**：结合人工智能和机器学习技术，提升模型对复杂系统动态变化的预测能力。
- **高效率计算**：优化算法结构，提高计算效率，以支持大规模数据分析和实时预测。
- **自适应学习**：建立自适应学习机制，使模型能自我调整以适应新的流行病学数据。

### 5.3.2 递归算法在构建未来疫情防控体系中的潜在价值

在构建未来的疫情防控体系中，递归算法具有以下潜在价值：

- **早期预警系统**：通过递归模型分析数据，及时发现疫情爆发的征兆，为早期干预提供依据。
- **个性化医疗干预**：结合个体健康数据和流行病学数据，为不同群体设计个性化的预防和治疗策略。
- **全球疫情监测网络**：构建一个全球性的疫情数据监测和分析网络，利用递归模型实现疫情的全球协同控制。

递归算法在新兴传染病预测和控制中的应用不仅具有理论价值，而且在实践中也显示出巨大的潜力。通过不断的技术创新和应用拓展，递归算法有望成为未来全球疫情防控体系的重要组成部分。

graph LR
    A[流行病学数据] -->|输入| B(递归模型)
    B -->|预测| C[疫情发展趋势]
    C -->|输出| D[早期预警]
    B -->|个人化| E[个性化医疗干预策略]
    B -->|数据分析| F[全球疫情监测网络]

在本章节中，我们深入探讨了递归算法在新兴传染病模型中的创新应用，通过模块化设计、集成多元数据源和多尺度建模等策略，使递归模型能够更好地应对新型传染病的挑战。同时，递归算法的智能化、高效率计算和自适应学习将成为其未来发展的关键技术趋势。通过这些发展，递归算法在建立早期预警系统、个性化医疗干预和全球疫情监测网络方面将展现出巨大的应用潜力，为未来全球疫情防控体系的构建提供有力支持。

# 6. 结论与展望：递归算法在传染病控制中的综合评价

## 6.1 递归算法对传染病解决方案的贡献总结

递归算法通过其对复杂问题的分解和逐级解决能力，在传染病的数据分析和预测中显示了显著的应用成效。在本小节中，我们首先将回顾递归算法在疫情数据分析和预测中的应用情况，并对其实际成效进行分析。接下来，我们评估递归模型对公共卫生决策的影响，以及它在疫情防控中所扮演的角色。

### 6.1.1 算法在疫情数据分析和预测中的应用成效

在数据分析方面，递归算法能够有效地对历史数据进行结构化分析，识别疫情传播的潜在趋势和模式。通过递归结构，我们可以构建起多层的疫情传播模型，每一层代表不同的传播阶段。例如，递归模型可以揭示一个地区的疫情是如何从零星爆发到形成群体感染，再到可能出现的疫情峰值和衰退期。这为公共卫生决策者提供了直观的数据支持。

让我们来看一个简化的代码示例，展示如何用递归算法对疫情数据进行简单的趋势分析：

def recursive_prediction(data, depth):
    if depth <= 0:
        return data[-1]
    else:
        # 假设data是一个包含每日新增病例数的列表
        # 这里简单使用前一天的数据来预测第二天的数据
        prediction = data[-1] * 1.05  # 预测增长率为5%
        return recursive_prediction(data + [prediction], depth - 1)

# 示例数据
past_data = [10, 20, 30, 40, 50]
# 进行5天的预测
predicted_data = recursive_prediction(past_data, 5)

在实际应用中，上述代码可以进一步复杂化以适应现实世界数据的波动性和不规则性，例如通过引入更多历史数据，以及考虑疫情传播的限制因素等。

### 6.1.2 递归模型对公共卫生决策的影响评估

递归模型为决策者提供了预测未来疫情走势的工具，这对于制定公共卫生策略至关重要。模型可以帮助评估不同的干预措施，比如社交距离、封锁措施、疫苗接种策略等对疫情发展的影响。通过对递归模型进行模拟和优化，可以找到最有效的疫情控制方案。

此外，递归模型也有助于识别疫情的脆弱群体和高风险地区，从而针对性地加强防控措施。例如，可以使用递归算法对不同群体的感染概率进行建模，并提出优先接种疫苗的对象。

## 6.2 递归算法在未来传染病研究中的前景与挑战

递归算法的未来发展对于应对传染病，尤其是可能出现的新兴传染病，具有重要的潜力。然而，在这一过程中，我们也会遇到一些科学和技术上的挑战。在本小节中，我们将探讨递归算法在未来传染病研究中的潜力，并讨论面临的主要挑战及应对策略。

### 6.2.1 递归算法在应对未来疫情的潜力探讨

随着数据分析技术的进步，递归算法将能更精确地模拟和预测传染病的传播。其潜力包括：

- **实时数据处理**：随着大数据技术的发展，递归模型能够处理实时传入的数据，从而提供更精确的预测。
- **机器学习的结合**：将递归算法与机器学习相结合，可以自动从数据中学习复杂模式，提高模型的预测能力。
- **多维度模型构建**：递归算法能够整合更多的变量（如社会经济因素、环境因素等），构建更全面的疫情传播模型。

### 6.2.2 面临的科学和技术挑战及应对策略

尽管递归算法在传染病控制中的应用前景广阔，但在实际应用中也面临着多方面的挑战：

- **数据的不完整性与不准确性**：实际中的疫情数据往往存在缺失和误差，需要发展更健壮的算法来处理这些问题。
- **模型的过度复杂化**：过于复杂的递归模型可能导致计算效率下降，需要在模型的精确度和效率之间找到平衡点。
- **不确定性的管理**：疫情发展的不确定性要求模型能够适应各种可能的情景，并提供相应的预测。

针对这些挑战，未来的研究应当集中在以下几个方向：

- **增强数据质量**：通过技术手段提升数据收集的准确性和完整性。
- **算法优化与创新**：开发更高效、更适应性强的递归算法。
- **情景模拟与决策支持系统**：构建多情景模拟系统，为政策制定者提供决策支持。

通过这些应对策略，递归算法将在未来传染病的研究和控制中扮演更加重要的角色。