【深度学习的激活函数选择】：权威指南与最佳实践

# 1. 深度学习激活函数基础

在深度学习领域，激活函数（Activation Function）扮演着至关重要的角色。激活函数使得神经网络可以模拟任意复杂的函数映射，从而解决非线性问题，如图像和语音识别，自然语言处理等。一个理想激活函数的关键特性包括非线性、可微性、单调性，并且计算效率要高。本章将从激活函数的基本概念和重要性入手，为读者揭开激活函数的神秘面纱。我们将介绍最基础的激活函数原理，以及如何在构建神经网络模型时选择合适的激活函数。通过理解激活函数的工作机制，读者将能够更好地掌握深度学习模型的构建与优化。接下来的章节将深入探讨激活函数的理论分析、比较与分析，以及优化技巧与实践。

# 2. 激活函数的理论分析

### 2.1 激活函数的数学原理

#### 2.1.1 神经网络中的非线性映射

在神经网络的训练过程中，激活函数扮演着至关重要的角色。为了理解其重要性，我们首先需要回顾一下神经网络的基本工作原理。神经网络由多层组成，每一层都包含若干个神经元，这些神经元之间相互连接并传递信息。激活函数正是作用在这些神经元上的非线性函数，其目的是向神经网络引入非线性因素。

非线性映射能力是深度学习区别于传统机器学习算法的关键特性之一。在没有激活函数的情况下，即使构建一个多层次的网络结构，网络也只能表示线性变换。这是因为多个线性变换的叠加仍然是线性的。而激活函数的引入打破了这种限制，使得网络可以近似表示任意复杂的函数，从而能够处理复杂的非线性问题。

#### 2.1.2 激活函数的梯度传播

梯度传播是激活函数在反向传播算法中的核心作用。在神经网络的训练过程中，通过不断调整网络参数（权重和偏置），使得网络输出误差最小化。这需要计算损失函数相对于网络参数的梯度，并利用链式法则反向传播更新参数。

在反向传播过程中，激活函数的梯度必须是可计算的，以便于梯度信息能够正确地传递回网络。然而，激活函数的梯度在某些情况下可能会导致梯度消失或梯度爆炸问题。梯度消失是指梯度随着反向传播逐渐减小，导致权重更新缓慢，网络难以收敛；而梯度爆炸则相反，梯度变得非常大，可能导致网络权重更新过大，进而影响模型的稳定性。

### 2.2 激活函数的历史演变

#### 2.2.1 早期激活函数回顾

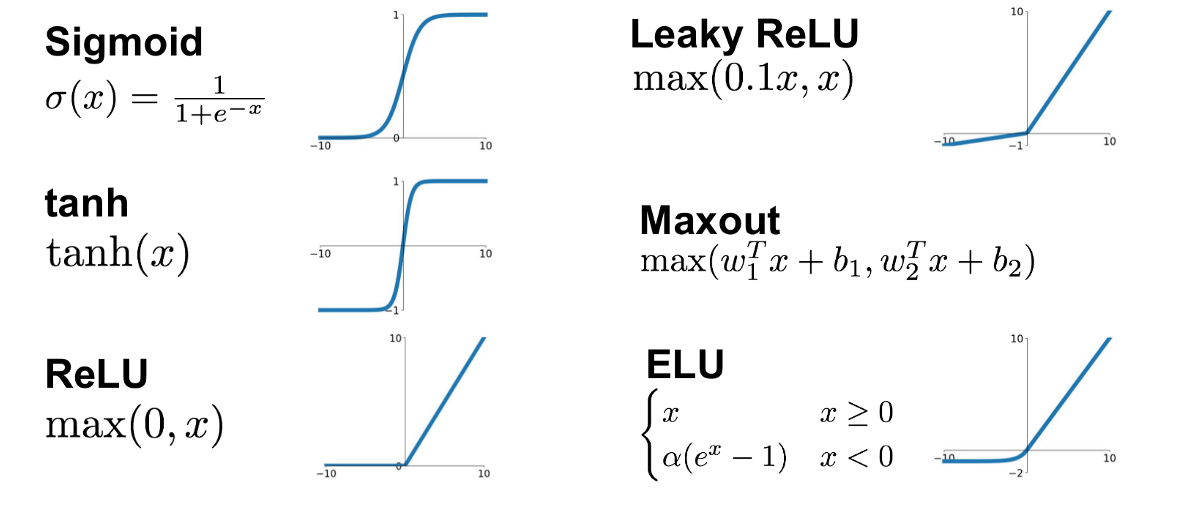
早期的神经网络研究中，激活函数的选择相对有限。一个典型的例子是Sigmoid函数，它具有良好的数学性质和生物学背景。Sigmoid函数的数学表达式为 `σ(x) = 1 / (1 + exp(-x))`，其输出范围为(0,1)，可以被解释为概率值。然而，Sigmoid函数存在梯度消失的问题，并且在两端的导数趋于0，使得网络难以有效训练。

另一个早期常用的激活函数是双曲正切函数（Tanh）。Tanh函数的输出范围在(-1,1)之间，其图像类似于Sigmoid函数，但中心点在原点。Tanh函数相对于Sigmoid的优势在于，其输出均值更接近于0，这有助于加速收敛过程。然而，Tanh函数同样面临梯度消失的问题。

#### 2.2.2 现代激活函数的兴起

随着深度学习研究的深入，研究人员不断探索新的激活函数以解决早期激活函数的问题。ReLU（Rectified Linear Unit）是这一领域的重大突破之一，它的数学表达式非常简单：`f(x) = max(0, x)`。ReLU在正区间内梯度为1，有效缓解了梯度消失的问题，并且计算效率高。然而，ReLU在负区间内梯度为0，这可能导致所谓的“死亡ReLU”问题，即一部分神经元可能会永久性地不激活。

为了克服ReLU的不足，研究人员提出了多种ReLU的变种，例如Leaky ReLU、Parametric ReLU（PReLU）等。Leaky ReLU通过给负区间赋予一个小的正斜率来避免死亡ReLU问题，而PReLU则将这个斜率作为学习参数，使得网络可以在训练过程中自动调整。

### 2.3 激活函数的关键性能指标

#### 2.3.1 梯度消失与梯度爆炸问题

梯度消失与梯度爆炸问题是激活函数在深度网络训练中需要面对的主要挑战之一。当网络层数增多时，梯度在反向传播过程中可能指数级地衰减或增长，这会严重阻碍网络参数的优化。

为了缓解梯度消失问题，研究人员提出了一系列方法，如使用ReLU激活函数、残差连接（Residual Connections）等。而梯度爆炸问题则可以通过梯度裁剪（Gradient Clipping）、权重初始化策略等方法来降低其影响。

#### 2.3.2 激活函数的选择标准

选择合适的激活函数对于构建有效的神经网络模型至关重要。在选择激活函数时，需要考虑多个因素，包括函数的非线性能力、梯度特性、计算效率以及是否易于实现等。

非线性能力决定了网络能否捕捉数据中的复杂模式；梯度特性影响着网络的训练效率和稳定性；计算效率则关系到网络在实际应用中的执行速度；易实现性则是从工程实践角度出发，考虑激活函数的实现是否简单，是否需要额外的计算资源等。

在实际应用中，没有一种激活函数适用于所有情况。通常需要根据具体任务和网络结构来选择最适合的激活函数。通过实验和经验积累，研究人员和工程师可以逐渐形成对不同激活函数优劣的直观理解，并据此做出合理的选择。

## 第三章：常用激活函数的比较与分析

### 3.1 Sigmoid和Tanh函数的分析

#### 3.1.1 Sigmoid函数的工作原理与局限性

Sigmoid函数是一个平滑的、S型的函数，它将任意实数值压缩到(0,1)区间内。数学表达式如下：

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 示例
x = np.array([-2, -1, 0, 1, 2])
print("Sigmoid函数的输出：", sigmoid(x))

Sigmoid函数的优势在于其数学形式简洁，以及在早期的概率模型和二分类问题中有良好的应用背景。然而，Sigmoid函数在两端的梯度接近于零，这会导致深层网络中的梯度消失问题，从而使得网络难以训练。此外，Sigmoid函数还存在输出均值不为零的问题，这可能导致梯度更新的不对称性，进一步影响收敛速度。

#### 3.1.2 Tanh函数的优势与不足

Tanh函数是Sigmoid函数的变体，其输出范围为(-1,1)，数学表达式为：

def tanh(x):
    return np.tanh(x)

# 示例
x = np.array([-2, -1, 0, 1, 2])
print("Tanh函数的输出：", tanh(x))

Tanh函数相较于Sigmoid函数的优势在于其输出均值为零，这有助于缓解梯度更新的不对称性问题。然而，Tanh函数仍然存在梯度消失的问题，并且其计算成本要高于Sigmoid函数，因为它需要进行更复杂的指数运算。

### 3.2 ReLU及其变种的详解

#### 3.2.1 ReLU函数的原理与优点

ReLU函数的出现标志着现代深度学习的崛起。ReLU函数的数学表达式为：

def relu(x):
    return np.maximum(0, x)

# 示例
x = np.array([-2, -1, 0, 1, 2])
print("ReLU函数的输出：", relu(x))

ReLU函数的优点在于其线性的、非饱和的正区间，这使得其在正区间内的梯度恒为1，极大地缓解了梯度消失问题。此外，ReLU函数的计算效率较高，因为其计算仅涉及比较操作。然而，ReLU函数在负区间内的梯度为零，这可能导致所谓的“死亡ReLU”问题，即神经元在训练过程中永久性失活。

#### 3.2.2 ReLU变种函数对比（Leaky ReLU、Parametric ReLU等）

为了克服ReLU函数在负区间梯度为零的缺点，研究人员提出了多种变体。Leaky ReLU是其中的一个例子，它通过为负区间赋予一个小的正斜率来避免死亡ReLU问题：

def leaky_relu(x, alpha=0.01):
    return np.where(x >= 0, x, alpha * x)

# 示例
x = np.array([-2, -1, 0, 1, 2])
print("Leaky ReLU函数的输出：", leaky_relu(x))

在Leaky ReLU中，参数alpha控制着负区间的斜率，通常是一个很小的常数，如0.01。Parametric ReLU（PReLU）则进一步将alpha作为学习参数，允许网络在训练过程中自动调整这一值。

### 3.3 其他激活函数探究

#### 3.3.1 Swish和Mish的兴起与应用

Swish和Mish是近年来提出的一些新的激活函数，它们试图在ReLU和其变种的基础上进一步改善性能。Swish函数的表达式为：

def swish(x):
    return x * sigmoid(x)

# 示例
x = np.array([-2, -1, 0, 1, 2])
print("Swish函数的输出：", swish(x))

Swish函数是由Google提出的一种自门控激活函数，它在正区间内表现类似ReLU，但在负区间内具有非零梯度，这有助于缓解死亡ReLU问题。Mish函数是Swish的变体，其表达式为：

def mish(x):
    return x * tanh(swish(x))

# 示例
x = np.array([-2, -1, 0, 1, 2])
print("Mish函数的输出：", mish(x))

Mish函数在设计上尝试结合了Tanh和Swish的优势，提供了平滑的激活曲线和非零梯度，被证明在多个深度学习任务中都有不错的表现。

#### 3.3.2 Softmax与Normalization层的区别

在讨论激活函数时，我们还需要区分一些概念，比如Softmax函数和Normalization层。Softmax函数通常在多分类问题的输出层使用，其目的是将一个固定长度的实数向量转换成概率分布。Softmax函数的数学表达式为：

def softmax(x):
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum(axis=0)

# 示例
x = np.array([1.0, 2.0, 3.0])
print("Softmax函数的输出：", softmax(x))

与激活函数不同，Softmax是一种归一化方法，它将输出值转换成概率形式，便于进行分类。而Normalization层，如Batch N