【神经网络性能优化】：激活函数在正则化中的角色与技巧

# 1. 神经网络激活函数的理论基础

激活函数在神经网络中扮演着至关重要的角色，它决定了神经网络能否学习并模拟复杂的非线性函数。理解激活函数的理论基础对于构建有效的神经网络模型至关重要。本章将从激活函数的基本概念开始，逐步深入探讨它们如何影响网络的性能。

## 1.1 激活函数的作用

激活函数引入了非线性因素，使得即使在多层网络中，网络的输出也能捕捉输入数据的复杂模式。在没有激活函数的情况下，无论网络有多少层，其表现始终是线性的，限制了模型的表达能力。

# 线性激活函数示例
import torch.nn as nn

class LinearModel(nn.Module):
    def __init__(self):
        super(LinearModel, self).__init__()
        self.linear = nn.Linear(in_features=10, out_features=1)
    def forward(self, x):
        return self.linear(x)

## 1.2 常见的激活函数类型

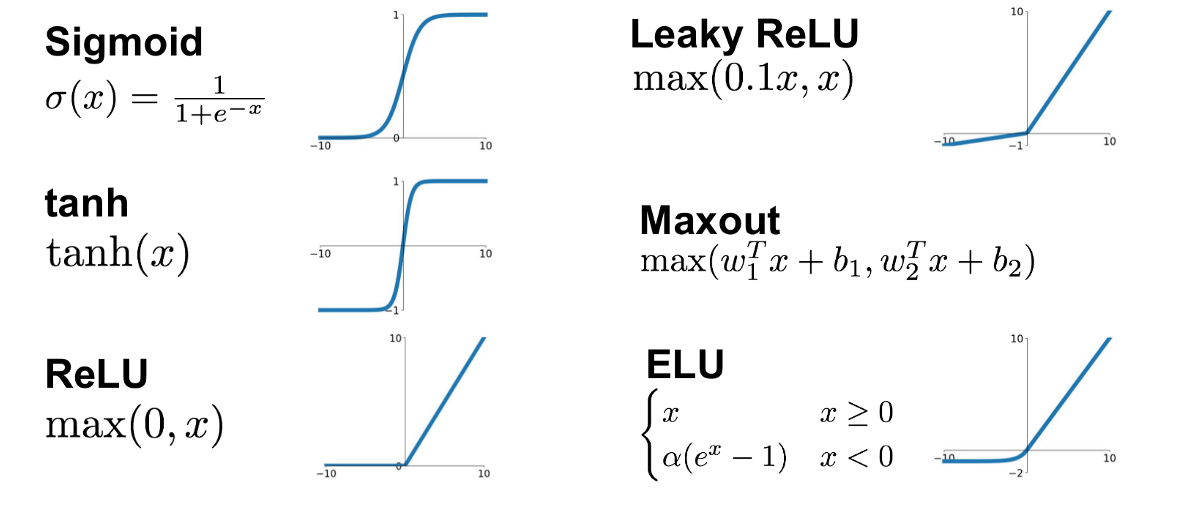
从历史上看，有许多类型的激活函数被提出和应用，包括但不限于 Sigmoid, Tanh, ReLU 等。每种激活函数都有其特点和适用场景。

- **Sigmoid**: 限制在0到1之间，但存在梯度消失问题。
- **Tanh**: 类似于Sigmoid，但输出限制在-1到1之间，同样有梯度消失问题。
- **ReLU** (Rectified Linear Unit): 提供非线性特性，更易于优化，但可能导致神经元“死亡”问题。

## 1.3 激活函数的选择标准

激活函数的选择直接影响到模型的训练效率和最终性能。通常，我们在实践中需要根据具体问题、数据集和网络结构综合考虑选择激活函数。

- **计算效率**: 一些激活函数计算速度更快，如ReLU。
- **梯度表现**: 梯度稳定性对防止训练过程中出现梯度消失或爆炸很重要。
- **网络特性**: 某些激活函数在特定类型的网络中表现出色，比如深度网络中ReLU系函数的应用。

通过本章的学习，我们可以了解到激活函数的基本原理以及其在构建和优化神经网络中的重要性。接下来，我们将深入探讨正则化技术如何与激活函数相互作用，共同提升神经网络的泛化能力。

# 2. 正则化技术及其在神经网络中的应用

## 2.1 正则化概念与方法

### 2.1.1 L1和L2正则化的基本原理

在机器学习和神经网络的训练过程中，正则化是一种防止模型过拟合的技术。它通过在损失函数中加入一个与模型复杂度相关的项，来惩罚模型参数的复杂性。L1和L2正则化是最常见的两种形式。

- **L1正则化（Lasso Regularization）**：通过加入权重的绝对值之和来控制模型复杂度，形式化表示为：

\[ J(\theta) = \frac{1}{m} \sum_{i=1}^m L(y^{(i)}, h_{\theta}(x^{(i)})) + \lambda \sum_{j=1}^n |\theta_j| \]

其中，\( \theta \) 表示模型参数，\( m \) 是训练样本数量，\( L \) 是损失函数（如均方误差），\( \lambda \) 是正则化参数，\( n \) 是特征数量。L1正则化会使某些参数变为零，从而实现特征选择。

- **L2正则化（Ridge Regularization）**：通过加入权重的平方和来控制模型复杂度，形式化表示为：

\[ J(\theta) = \frac{1}{m} \sum_{i=1}^m L(y^{(i)}, h_{\theta}(x^{(i)})) + \lambda \sum_{j=1}^n \theta_j^2 \]

L2正则化倾向于使参数值接近于零但不完全为零，对模型参数施加一个温和的惩罚，通常不会导致参数稀疏。

### 2.1.2 其他正则化技术概述

除了L1和L2正则化之外，还有其他一些正则化技术，如：

- **Elastic Net**：结合了L1和L2正则化，它同时考虑了特征选择和对权重大小的惩罚。形式化表示为：

\[ J(\theta) = \frac{1}{m} \sum_{i=1}^m L(y^{(i)}, h_{\theta}(x^{(i)})) + \lambda_1 \sum_{j=1}^n |\theta_j| + \lambda_2 \sum_{j=1}^n \theta_j^2 \]

- **Dropout**：这种方法在训练过程中随机“丢弃”一部分神经元，即暂时将它们从网络中移除，这可以防止神经元对特定训练样例的依赖，从而增加网络的泛化能力。

- **Data Augmentation**：数据增强通过对训练数据进行一些变换来增加数据集的大小，这有助于模型学习到更加鲁棒的特征。

## 2.2 正则化在神经网络中的角色

### 2.2.1 防止过拟合

过拟合是神经网络训练中的一个常见问题，它发生在模型在训练数据上表现良好，但在未见过的数据上表现糟糕的情况。正则化通过限制模型复杂度来防止过拟合，从而提高模型在测试数据上的表现。

### 2.2.2 提升模型泛化能力

正则化通过在损失函数中增加一个与模型复杂度相关的惩罚项，鼓励模型学习更加简单和泛化的特征表示。这样不仅有助于提高模型在训练集上的性能，而且更重要的是提高模型在新数据上的预测能力。

## 2.3 正则化与激活函数的相互作用

### 2.3.1 激活函数对正则化效果的影响

激活函数的选择直接影响到神经网络的训练过程以及正则化的效率。例如，使用ReLU激活函数时，由于其线性特性，L2正则化通常比L1正则化表现更好。这是因为ReLU在正区域是线性的，而L1惩罚则对线性区域没有影响。

### 2.3.2 选择合适的激活函数以增强正则化

在设计神经网络时，选择合适的激活函数可以增强正则化的效果。例如，当使用L2正则化时，推荐使用ReLU或其变种，如Leaky ReLU或Parametric ReLU，因为它们有助于缓解梯度消失问题，并促进更有效的训练过程。

激活函数和正则化方法的选择应当根据具体任务的需求和数据集的特性进行调整。例如，在处理具有稀疏特征的数据时，L1正则化可能更有效；而在需要保持模型参数平滑时，L2正则化可能更为合适。通过实验和模型验证，可以确定最适合问题的正则化和激活函数组合。

# 3. 激活函数的性能评估与选择

在神经网络中，激活函数扮演着至关重要的角色，它赋予网络非线性特性，使模型能够学习和执行更复杂的任务。激活函数的性能直接影响到网络的训练效率和最终的预测性能。因此，激活函数的选择和评估是深度学习领域一个重要的研究课题。

## 3.1 常见激活函数对比分析

### 3.1.1 Sigmoid、Tanh、ReLU等函数特性

Sigmoid函数，也称为逻辑函数，其数学表达式为`f(x) = 1 / (1 + e^(-x))`，其输出范围在0到1之间。Sigmoid函数在历史上被广泛使用，但由于其在输入值极端时梯度接近于零的特性（梯度消失问题），在深层网络中使用时会导致训练速度缓慢。

Tanh（双曲正切函数）具有与Sigmoid相似的形状，但其输出范围是在-1到1之间，因此在原点附近具有更强的梯度。尽管如此，Tanh函数同样会遇到梯度消失问题，特别是在深层网络中。

ReLU（线性整流单元）函数定义为`f(x)