【激活函数创新】：探索深度学习新激活函数及其应用

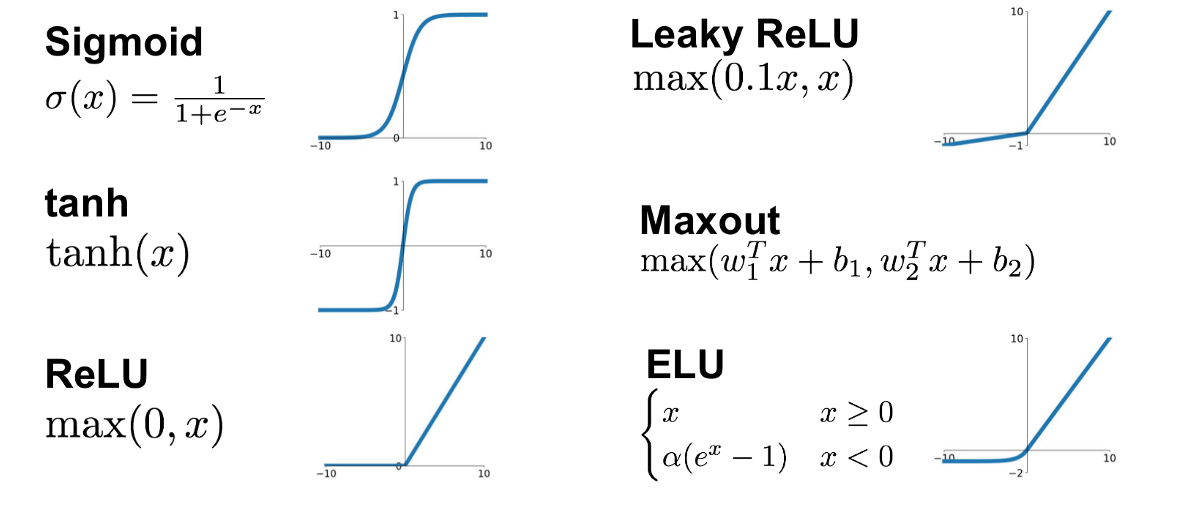
# 1. 深度学习激活函数概述

激活函数是深度学习中一个关键的组成部分，它们在神经网络中扮演着模拟复杂决策边界的角色。本章节将对激活函数进行初步介绍，为读者构建一个基础的理解框架。

## 1.1 激活函数的基本概念
激活函数是神经网络中用于添加非线性因素的函数，其主要目的是决定神经元是否应该被激活。它允许神经网络学习和执行更复杂的任务，如图像识别和自然语言处理。

## 1.2 激活函数的重要性
没有激活函数的网络是一个线性模型，而线性模型的表达能力有限，无法捕捉数据中的非线性特征。激活函数的引入使得网络能够学习更复杂的模式，从而提高模型的预测准确性。

## 1.3 激活函数的发展历程
从早期的Sigmoid和Tanh函数到现代的ReLU及其变种，激活函数的发展反映了神经网络结构和训练策略的进步。随着研究的深入，激活函数正变得更加多样化和专业化，以适应不同的网络结构和应用需求。

graph LR
A[激活函数概述] --> B[基本概念]
A --> C[激活函数重要性]
A --> D[发展历程]

# 2. 激活函数的理论基础与数学模型

### 2.1 激活函数在神经网络中的作用

#### 2.1.1 理解激活函数的必要性

激活函数是神经网络中的核心组成部分，它决定了网络的表达能力和非线性处理能力。神经网络通过层与层之间的线性组合来提取特征，但仅依靠线性运算，网络将无法捕捉到数据中的复杂模式和关系。因此，激活函数被引入到神经元的输出中，以提供非线性变换，使得网络能够逼近任意复杂的函数。

在没有激活函数的情况下，无论神经网络有多少层，最终都可以被简化为一个单层线性模型，这极大地限制了模型的表达能力。引入非线性激活函数后，即使网络只有两层，也能实现复杂的非线性映射。这也是为什么激活函数被认为是深度学习中的“魔法”所在。

### 2.2 常见激活函数的数学表达与特性

#### 2.2.1 Sigmoid函数及其导数

Sigmoid函数是一种最早被使用的激活函数之一，其数学表达式为：

\sigma(x) = \frac{1}{1 + e^{-x}}

Sigmoid函数将任意值压缩到(0, 1)区间内，这使得它在早期的二分类问题中非常流行，因为输出可以被解释为概率。然而，Sigmoid函数存在一些缺陷，比如输出不是零中心的，并且在两端的梯度接近于零，这会导致梯度消失问题。

Sigmoid函数的导数为：

\sigma'(x) = \sigma(x)(1 - \sigma(x))

#### 2.2.2 Tanh函数的优势与局限

Tanh（双曲正切）函数是Sigmoid函数的改进版，它的数学表达式为：

\tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}

Tanh函数的输出范围是(-1, 1)，比Sigmoid函数的(0, 1)范围更广，更接近于零中心。虽然Tanh解决了Sigmoid的一些问题，但它仍然存在梯度消失的问题，尤其在大数值输入的情况下。

Tanh函数的导数为：

\tanh'(x) = 1 - \tanh^2(x)

#### 2.2.3 ReLU及其变种的原理与特点

ReLU（Rectified Linear Unit）函数及其变种是目前最流行和广泛使用的激活函数，其基本形式为：

f(x) = max(0, x)

ReLU函数极大地缓解了梯度消失的问题，并且计算效率高，因为它只涉及一个阈值操作。然而，ReLU函数也有自身的缺点，比如“死亡ReLU”问题，即神经元可能永远不被激活，导致无法从训练中恢复。

为了克服ReLU的问题，研究人员提出了多种变种，如Leaky ReLU、Parametric ReLU等。Leaky ReLU尝试给予负部分一个较小的斜率，以保持梯度不为零：

f(x) = 
\begin{cases} 
x & \text{if } x > 0 \\
\alpha x & \text{if } x \leq 0
\end{cases}

其中，α是一个较小的常数。

### 2.3 激活函数的选择标准与优化目标

#### 2.3.1 激活函数性能的评估指标

激活函数的选择标准通常基于它们对模型性能的影响。一些重要的评估指标包括：

1. **收敛速度**：激活函数应该保证网络能够快速收敛，以缩短训练时间。
2. **梯度传播能力**：激活函数应确保在反向传播时，梯度能够有效地传播到每一层，以促进有效学习。
3. **防止梯度消失或爆炸**：选择激活函数时要确保其导数不会在训练过程中趋于零或无限大。

#### 2.3.2 激活函数的优化方向

优化激活函数的目标是找到一种既能提高模型性能又能保持计算效率的函数。目前的研究方向包括：

1. **探索更多非线性激活函数**：通过数学分析和实验研究，开发出新的激活函数。
2. **自适应激活函数**：让激活函数根据数据和模型的状态动态调整其参数。
3. **减少计算复杂度**：设计简单高效的激活函数，以减少计算成本并加速模型部署。

下一章节将对创新激活函数进行探索与实践，我们将详细讨论在设计和应用新激活函数时遇到的挑战、解决方案和实际案例。

# 3. 创新激活函数的探索与实践

随着深度学习技术的快速发展，传统的激活函数已不能满足复杂任务的需求。从理论上讲，激活函数需要具备非线性映射能力，但现有函数如Sigmoid和Tanh存在饱和问题，ReLU及其变种在某些情况下会面临死亡ReLU问题。因此，对激活函数的创新探索已成为研究热点，涉及设计思路的革新、实验验证以及应用场景的探索。

## 3.1 新激活函数的动机与设计思路

### 3.1.1 现有激活函数的不足

现有的激活函数在特定条件下可能面临各种问题，比如在深层神经网络中，Sigmoid和Tanh函数由于其导数接近于零的特性会导致梯度消失的问题，而ReLU函数则可能因为某些神经元输出为零而导致这些神经元“死亡”，从而不再对任何数据有反应。

### 3.1.2 创新激活函数的设计理念

为解决现有激活函数的局限性，新激活函数的设计理念聚焦于提高其非饱和性、改善梯度传播特性和增强网络的表达能力。例如，Swish函数引入了自我门控机制，通过结合输入信号和Sigmoid函数来动态调节激活值，从而缓解了ReLU类激活函数的"死亡"问题。

## 3.2 新激活函数的实验与分析

### 3.2.1 实验设置与测试基准

在探索新激活函数时，研究者通常会使用各种基准数据集和网络结构，例如CIFAR-