【数据科学实战】：时间序列异常检测的6个关键步骤

# 1. 时间序列异常检测概述

时间序列异常检测是数据分析领域的一个重要分支，它关注于从随时间变化的数据中识别出不符合预期的异常点或模式。在监控系统、金融服务、网络流量管理等领域，这种技术可以用来快速发现异常行为，从而及时采取措施以避免潜在的风险和损失。

本章将简要介绍时间序列异常检测的基本概念、常见的应用场景以及其在现代数据分析中的重要性。我们将探讨一些基本的异常检测方法，包括统计方法和基于机器学习的高级技术，为读者提供一个概览，进而深入到第二章，对时间序列数据本身进行更细致的了解和分析。

# 2. 理解时间序列数据

### 2.1 时间序列数据的特点

#### 2.1.1 时间的依赖性
时间序列数据中的时间依赖性是指一个数据点（例如一天的股票价格）可能会受到之前时间点数据的影响。例如，在股市中，今日的股价变动很可能是由昨日收盘价及之前历史价格影响的。理解这一点对于建模非常重要，因为许多时间序列分析方法，如自回归模型，就是基于这种时间依赖性。下面是理解时间依赖性所需的步骤：

1. **识别滞后项**：找出数据中对当前值有影响的历史数据点。
2. **自相关分析**：通过自相关图（ACF）和偏自相关图（PACF）分析这些滞后项。
3. **建立模型**：使用如ARIMA等模型来捕获这种依赖性，并用于预测。

代码示例（Python使用statsmodels库计算ACF和PACF）:

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import acf, pacf

# 假设df是包含时间序列数据的DataFrame
series = df['stock_price']

lag_acf = acf(series, nlags=20)  # 计算20个滞后项的ACF值
lag_pacf = pacf(series, nlags=20, method='ols')  # 计算20个滞后项的PACF值

# 绘制ACF和PACF图
plt.figure(figsize=(12, 6))

plt.subplot(121)
plt.plot(lag_acf)
plt.axhline(y=0, linestyle='--', color='gray')
plt.axhline(y=-1.96/np.sqrt(len(series)), linestyle='--', color='gray')
plt.axhline(y=1.96/np.sqrt(len(series)), linestyle='--', color='gray')
plt.title('ACF Plot')

plt.subplot(122)
plt.plot(lag_pacf)
plt.axhline(y=0, linestyle='--', color='gray')
plt.axhline(y=-1.96/np.sqrt(len(series)), linestyle='--', color='gray')
plt.axhline(y=1.96/np.sqrt(len(series)), linestyle='--', color='gray')
plt.title('PACF Plot')

plt.tight_layout()
plt.show()

#### 2.1.2 季节性和趋势
时间序列数据可能显示出季节性变化和趋势。季节性是指数据在特定时间段内重复出现的模式，例如，零售业的销售额在假日季节通常会有上升。趋势则表示数据随时间的总体上升或下降趋势。

识别季节性和趋势的方法包括：

1. **趋势分解**：使用如Loess分解技术将时间序列分解为趋势、季节性和随机成分。
2. **季节性调整**：通过去除季节性成分来使数据平稳，以便进行分析和预测。
3. **季节性预测**：一旦识别出季节性，就可以在模型中加以利用以改善预测。

代码示例（Python中使用seasonal_decompose）:

from statsmodels.tsa.seasonal import seasonal_decompose

result = seasonal_decompose(series, model='multiplicative')
result.plot()
plt.show()

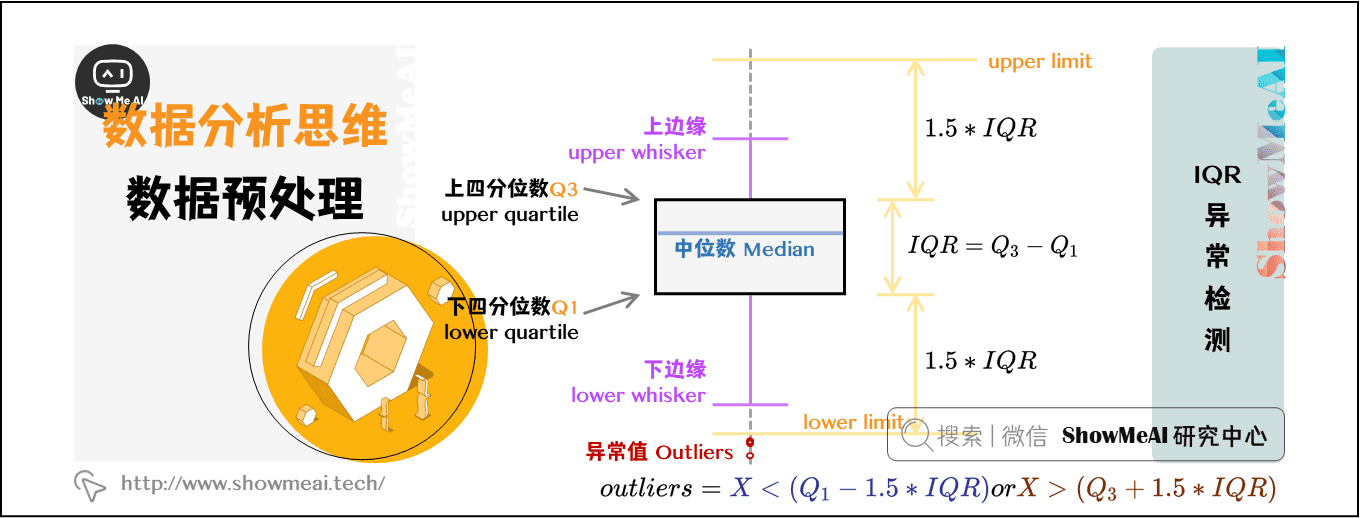
### 2.2 数据预处理

#### 2.2.1 缺失值处理
时间序列数据中可能包含缺失值，这些缺失值可能是由各种原因造成的，比如数据收集失败。处理缺失值的方法很多，包括：

1. **删除含有缺失值的记录**：简单但可能导致信息丢失。
2. **向前或向后填充**：用最近的有效值替代缺失值。
3. **插值**：使用如线性插值等方法估计并填充缺失值。

代码示例（使用向前填充方法）:

# 假设df是包含时间序列数据的DataFrame
df.fillna(method='ffill', inplace=True)

#### 2.2.2 异常值识别初步
异常值可能严重扭曲分析和预测结果。初步识别异常值通常涉及计算统计指标，如均值、标准差，并利用这些指标确定异常值的范围。例如，超出3倍标准差的点通常被认为是异常值。

代码示例（识别并标记异常值）:

mean = series.mean()
std = series.std()

# 定义异常值的范围
lower_bound = mean - 3 * std
upper_bound = mean + 3 * std

# 标记异常值
outliers = series[(series < lower_bound) | (series > upper_bound)]
print(outliers)

#### 2.2.3 数据的归一化和标准化
归一化和标准化是减少数据集内部差异的方法，它们可以增强模型性能并加速收敛过程。常见的方法包括：

1. **最小-最大归一化**：将数据按比例缩放，使之落入特定的范围，如[0,1]。
2. **Z-score标准化**：通过减去均值并除以标准差来转换数据，使其具有0均值和单位方差。

代码示例（最小-最大归一化和Z-score标准化）:

from sklearn.preprocessing import MinMaxScaler, StandardScaler

# 最小-最大归一化
min_max_scaler = MinMaxScaler()
series_minmax = min_max_scaler.fit_transform(series.values.reshape(-1, 1))

# Z-score标准化
standard_scaler = StandardScaler()
series_zscore = standard_scaler.fit_transform(series.values.reshape(-1, 1))

### 2.3 数据的探索性分析

#### 2.3.1 绘制时间序列图
时间序列图是时间序列分析中的基础工具，它帮助我们可视化数据随时间变化的趋势和周期性。Python的matplotlib库可以轻松绘制时间序列图：

plt.figure(figsize=(10,5))
plt.plot(series)
plt.title('Time Series Plot')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()

#### 2.3.2 统计描述和分布分析
进行统计描述和分布分析可以帮助我们理解数据的集中趋势、分散程度以及分布形态。这包括计算均值、中位数、标准差等。

代码示例（使用Pandas的描述性统计函数）:

print(series.describe())

以上各小节均展示了时间序列数据的探索性分析和预处理的详细步骤。在进一步的分析和模型构建前，这些步骤是基础且至关重要的。在时间序列数据处理的下一阶段，我们将深入探讨统计方法和机器学习技术在异常检测中的应用。

# 3. 时间序列异常检测的统计方法

## 3.1 经典统计检测方法

### 3.1.1 Z-得分
Z-得分是一种统计度量，用于衡量单个数据点偏离其数据集的均值的标准差数。在时间序列异常检测中，它用于识别那些超出正常波动范围的点。公式如下：

\[ Z = \frac{(X - \mu)}{\sigma} \]

其中 \(X\) 是观察值，\(\mu\) 是均值，\(\sigma\) 是标准差。

这种方法假定时间序列数据遵循正态分布。在正常条件下，Z值会落在-3到+3的范围内，超过这个范围的点通常被认为是异常值。

#### 代码示例与解释

import numpy as np

# 生成一个具有正态分布的随机时间序列
data = np.random.normal(0, 1, 1000)

# 计算均值和标准差
mean = np.mean(data)
std_dev = np.s