数据子集划分技术：交叉验证背后的数学原理：深入理解交叉验证背后的数学原理

# 1. 数据子集划分技术概述

在机器学习和统计学领域，数据子集划分技术是用来评估学习算法性能的一种关键技术。它的核心思想是将原始数据集分割为训练集和测试集，从而可以对学习算法的泛化能力进行科学的测量。这一过程不仅关乎到算法的验证与测试，还涉及到模型选择、参数调优以及防止模型过拟合等重要方面。对于任何数据科学项目来说，恰当地划分数据子集是构建准确、可靠模型的基石。

## 1.1 为什么要进行数据划分

数据子集划分是确保模型在未知数据上泛化能力的基础步骤。如果没有合理的划分，模型可能只是简单地记忆了训练数据中的特征，而不是学习到背后的规律，这将导致在新数据上的性能急剧下降。划分数据集有助于我们从两个维度评估模型性能：**训练误差**（模型在训练集上的表现）和**泛化误差**（模型在未见过的数据上的表现）。

## 1.2 数据子集的常见划分方法

数据集的划分通常会涉及到以下几种方法：

- **简单划分**：按照一定比例随机将数据分为训练集和测试集。这种方法实现简单，但在数据量较少的情况下容易导致过拟合或欠拟合。
- **分层划分**：在保持类别比例的情况下进行划分，适用于类别不平衡的数据集。通过确保每个子集中的类别分布与原始数据集相同，可以使得每个子集都具有良好的代表性。
- **时间序列划分**：在时间序列数据中，测试集通常是按照时间顺序位于训练集之后，以避免未来的信息泄漏到过去的数据中。

通过上述划分方法，能够确保评估的准确性和公正性，从而使得评估结果更有指导意义。在接下来的章节中，我们将深入了解交叉验证的理论基础及其在实际中的应用，探索这一核心数据科学概念的深度与广度。

# 2. 交叉验证的理论基础

## 2.1 统计学中的验证方法论

### 2.1.1 训练集与测试集的概念

在机器学习与统计学中，为了评估模型在未知数据上的表现，将数据分为训练集和测试集是至关重要的一步。训练集用于模型的构建和调整，而测试集则用于最终的评估。

训练集（Training Set）是用于模型学习和参数优化的数据集。它包含输入特征（Independent Variables）和对应的输出（Dependent Variables），模型通过这部分数据学习到的数据规律用于预测未知数据。

测试集（Test Set）则是用来独立评估模型性能的数据集。理想情况下，模型不应该在训练过程中接触到测试集中的任何数据。测试集用于提供一个客观的评价标准，以确定模型在未知数据上的泛化能力。

### 2.1.2 泛化误差的定义及其重要性

泛化误差（Generalization Error）是指模型在未见过的数据上的预期表现与实际表现之间的差异。这是衡量模型实际应用价值的关键指标。

计算泛化误差需要模型在独立的测试集上进行预测，并与真实值进行比较。泛化误差的大小取决于模型的复杂度、训练数据的代表性，以及学习算法的性能。

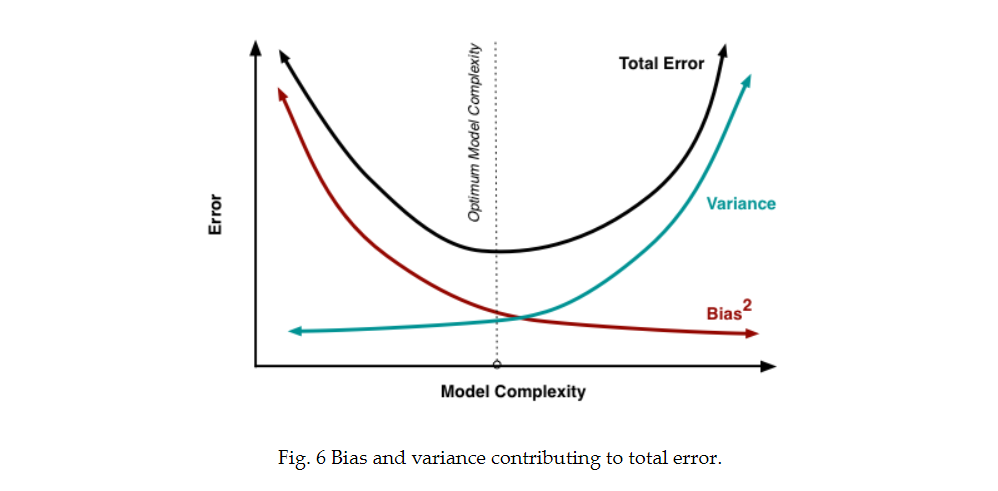
一个模型的泛化误差可以分为两个部分：偏差（Bias）和方差（Variance）。偏差是指模型对训练数据的平均预测与真实值之间的差异，它反映了模型的预测能力。方差则衡量了模型在不同训练数据集上的预测波动，它体现了模型的稳定性和对训练数据变化的敏感性。

## 2.2 交叉验证的基本原理

### 2.2.1 K折交叉验证的工作流程

K折交叉验证（K-Fold Cross-Validation）是评估泛化能力的一种常用方法。其核心思想是将数据集分割成K个大小相等的子集，每次使用其中的K-1个子集作为训练数据，剩余的1个子集作为测试数据，然后重复K次，最后计算所有K次测试结果的平均值作为最终评估。

K折交叉验证的流程如下：
1. 将数据集随机分成K个大小相等的子集。
2. 对于每一个子集，依次作为一次验证集，其余K-1个子集组成训练集。
3. 在每一次迭代中，使用训练集训练模型，并在验证集上评估模型的性能。
4. 记录每一次的评估指标，如准确率、召回率或F1分数。
5. 计算K次迭代评估指标的平均值。

### 2.2.2 抽样策略与数据分布的关系

K折交叉验证的效果很大程度上取决于数据的抽样策略。合理的抽样能够确保训练集和测试集的数据分布尽可能接近总体数据分布。

在选择抽样策略时，需要考虑以下因素：
- 数据是否具有时间顺序，例如时间序列数据，这时应确保样本顺序不会被破坏。
- 数据集是否平衡，对于分类问题，每个类别的样本是否都得到了足够的代表。
- 数据是否具有内在的分组结构，如不同医院的病人数据，这种情况下需要考虑分层抽样。

## 2.3 交叉验证中的数学假设

### 2.3.1 独立同分布的假设

交叉验证的理论基础之一是独立同分布（Independently and Identically Distributed, i.i.d）假设。该假设意味着训练集中的数据与测试集中的数据都是独立同分布的。

对于i.i.d假设，有以下要点：
- **独立性**（Independence）：数据集中的每个样本都是独立抽取的，样本之间没有依赖关系。
- **同分布性**（Identically Distributed）：每个样本都是从同一个概率分布中抽取的。

在实际应用中，独立同分布的假设往往难以完全满足。例如，时间序列数据由于其时间依赖性，通常不能被视为独立同分布。在这些情况下，交叉验证可能需要采用特殊的处理方法，如时间序列交叉验证（Time Series Cross-Validation）。

### 2.3.2 算法的一致性和收敛性

一致性和收敛性是衡量算法好坏的重要指标，它们指的是随着数据量的增加，算法能否最终收敛到真实的模型参数。

**一致性**（Consistency）：如果一个算法是一致的，那么当数据量趋于无穷大时，算法得到的模型参数会收敛于真实的参数值。

**收敛性**（Convergence）：算法的收敛性描述了算法在有限的迭代次数内，能否收敛到最优解或者一个足够好的解。

在使用交叉验证时，了解算法的一致性和收敛性对于选择合适的交叉验证策略和评估模型性能至关重要。如果算法的一致性和收敛性较差，交叉验证的评估结果可能会受到影响，导致对模型性能的误判。

## 代码块展示及解释

from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score

# 定义一个数据集和对应的标签
X = [[1, 2], [3, 4], [1, 3], [4, 3], [2, 4], [2, 3]]
y = [0, 1, 0, 1, 1, 1]

# 初始化随机森林分类器
clf = RandomForestClassifier(n_estimators=100)

# 初始化K折交叉验证器，设置折数为3
kf = KFold(n_splits=3)

# 对每一折进行模型训练和预测，并计算准确率
for train_index, test_index in kf.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]
    clf.fit(X_train, y_train)  # 在训练集上训练模型
    predictions = clf.predict(X_test)  # 在测试集上进行预测
    print(f"Accuracy: {accuracy_score(y_test, predictions)}")

在上述代码中，我们首先从`sklearn.model_selection`导入了`KFold`类，用于实施K折交叉验证。接着，创建了一个简单的随机森林分类器实例。

对于K折交叉验证的每一次迭代，我们通过`split`方法对数据集`X`进行了分割，得到了训练集和测试集的索引。然后，我们使用这些索引提取相应的训练和测试数据，并将训练数据输入到分类器中进行训练。最后，使用训练好的模型对测试数据进行预测，并通过`accuracy_score`计算出准确率。

代码块演示了如何实际使用交叉验证来评估模型的性能。通过循环中的每次迭代，我们能够了解模型在不同数据子集上的表现。最终的准确率输出反映了模型的平均表现，可以作为模型泛化能力的一个估计。

# 3. 交叉验证的数学模型解析

## 3.1 交叉验证的期望风险估计
### 3.1.1 期望风险的数学定义
在交叉验证中，期望风险估计是衡量模型泛化能力的关键指标。它定义为模型在独立同分布的未知数据上的平均损失。数学上，期望风险表示为一个概率测度下的积分，这个测度对应于数据生成过程。

给定损失函数L，模型f，数据分布P(X,Y)，期望风险R(f)可以表示为：

\[ R(f) = \mathbb{E}_{(X,Y) \sim P}[L(Y, f(X))] \]

其中\( \mathbb{E} \)表示期望算子，\( (X,Y) \)是随机变量对，代表输入数据及其对应的真实标签，f是我们的学习模型。

### 3.1.2 风险估计的偏差和方差分析
在实际操作中，由于无法访问真实的分布P，我们使用有限的样本数据集\( D = \{(x_i,y_i)\}_{i=1}^n \)来估计期望风险。这就引入了偏差和方差两个概念。

偏差代表了估计值与真实期望风险之间的系统误差，方差衡量了估计值自身的波动程度。高偏差意味着模型可能未很好地拟合数据，而高方差通常表示模型对数据中的噪声过于敏感。

理想情况下，我们希望得到一个偏差和方差都尽可能低的风险估计。然而，在实践中，模型复杂度与偏差和方差之间往往存在一种权衡关系，即所谓的偏差-方差权衡。

## 3.2 交叉验证的方差分解
### 3.2.1 方差分解的基本原理
方差分解帮助我们理解交叉验证估计量的稳定性。在交叉验证中，将数据分成k个部分，每次使用其中一个部分作为测试集，其余作为训练集。方