递归树与动态规划：解决复杂问题的黄金组合

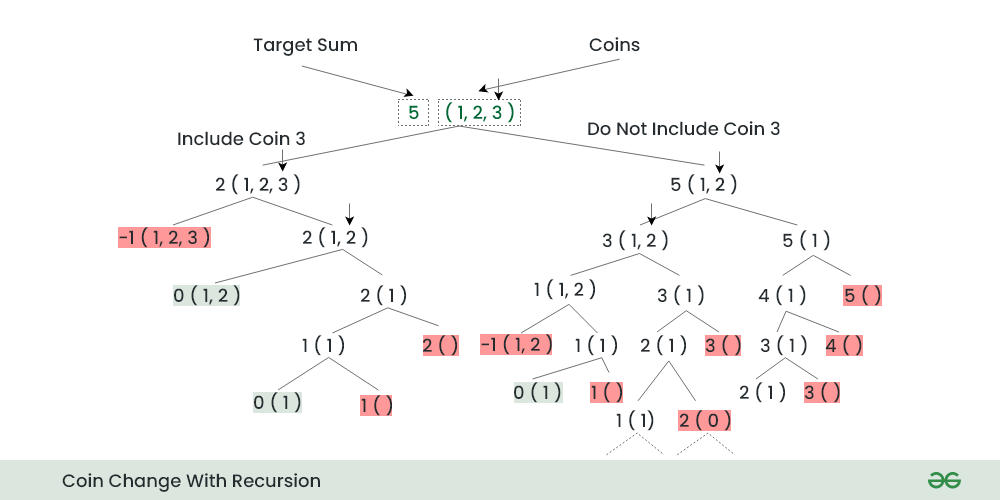
# 1. 递归树与动态规划概述

在计算机科学和数学的领域，递归树与动态规划是两种不同的但彼此紧密相关的技术，它们被广泛应用于解决复杂问题。递归树以树状结构直观地展示递归过程，动态规划则是一种通过将问题分解为相互重叠的子问题来求解最优解的方法。

## 递归树与动态规划的关联

递归树和动态规划在处理问题时，都涉及到将问题拆分成更小的子问题。但是，递归树更强调问题分解的结构化展示，而动态规划则注重从子问题的解决中提炼出有效的计算策略，避免重复计算，提高效率。

## 应用场景

递归树在理解和推导动态规划算法的过程中起着辅助作用，它可以帮助我们形象地理解子问题的依赖关系。动态规划则更多用于实际算法设计，尤其是在处理具有重叠子问题结构的优化问题时，比如资源分配、路径选择等问题。

# 2. 递归树的基本理论与应用

## 2.1 递归的基本概念
在计算机科学中，递归是一种常见的编程技术，它允许一个函数直接或间接地调用自身。递归有两个主要部分：基本情况（base case）和递归步骤（recursive step）。基本情况是递归调用的停止条件，而递归步骤则是函数调用自身来解决问题的更小部分。

### 2.1.1 递归的基本概念
递归的典型例子是计算阶乘：

def factorial(n):
    if n == 0:  # 基本情况
        return 1
    else:  # 递归步骤
        return n * factorial(n - 1)

在这段代码中，`factorial(5)` 会逐步展开为 `5 * factorial(4)`, `5 * 4 * factorial(3)`，直到 `5 * 4 * 3 * 2 * 1 * factorial(0)`，最终达到基本情况并返回1。

### 2.1.2 递归树的结构与表示
递归树是递归过程的视觉表示。在递归树中，每个节点代表一次函数调用，子节点表示该函数的递归调用。树的根节点是最初的问题，而叶节点则是基本情况。

一个计算阶乘的递归树如下所示：

                           f(5)
                        /       \
                     f(4)        f(4)
                    /   \        /   \
                 f(3)    f(3) f(3)   f(3)
                /   \     /    \      /  \
              f(2) f(2) f(2)  f(2) f(2) f(2)

在树中，每一层表示一次递归调用的展开，直到到达叶节点，即基本情况。

## 2.2 递归树的构建方法
构建递归树的方法主要分为两大类：自顶向下和自底向上。

### 2.2.1 自顶向下的构建策略
自顶向下的方法从问题的总体目标开始，并逐步分解到小的子问题。在自顶向下的递归树构建中，我们从树的根节点开始，每次递归调用产生分支。

### 2.2.2 自底向上的构建策略
与自顶向下不同，自底向上的策略从最小的子问题开始，并将它们合并形成更大的问题，直至达到最终问题的解。在自底向上的递归树构建中，我们从叶节点开始，每一步合并为上一层的节点。

## 2.3 递归树在问题解决中的作用
递归树对于理解和解决复杂的递归问题非常有用，尤其是那些可以通过分解为更小相似问题来解决的问题。

### 2.3.1 分解复杂问题
递归树帮助我们可视化问题如何被分解为更小的子问题，每个子问题都可以单独解决。分解有助于简化复杂的问题，并使解决方案更加清晰和易于理解。

### 2.3.2 递归与回溯的实例分析
递归树可以用于分析和设计回溯算法，回溯算法是一种通过递归来尝试每一种可能的解直到找到所需的解或者确定不存在解为止的过程。

例如，在解决N皇后问题时，递归树的每个节点代表棋盘上放置皇后的决策过程，递归步骤则是尝试在下一行放置皇后。通过剪枝（即不考虑某些不可能产生解的路径），我们可以有效地减少搜索空间，从而提高算法的效率。

递归树的构建与分析是理解递归算法的重要步骤，它不仅帮助我们设计递归解法，还允许我们优化和改进递归算法的性能。在下一章中，我们将进一步探讨动态规划，它是一种利用递归树思想来解决具有重叠子问题和最优子结构特性的问题的方法。

# 3. 动态规划的理论框架

动态规划（Dynamic Programming, DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学等领域中，用来解决多阶段决策过程优化问题的方法。它将复杂问题拆分为更小的子问题，并通过存储子问题的解，避免重复计算，最终达到解决原问题的目的。在本章中，我们将深入探讨动态规划的核心理论、算法设计、复杂性分析等方面，为读者提供一个全面的动态规划理论框架。

## 3.1 动态规划的基本原理

动态规划解决的问题往往具有两个重要的数学特性：最优子结构（Optimal Substructure）和重叠子问题（Overlapping Subproblems）。理解这两点是掌握动态规划的关键。

### 3.1.1 最优子结构与重叠子问题

**最优子结构**指的是一个整体的最优解包含其子问题的最优解。这意味着，问题的最优解可以从其子问题的最优解构造出来。在动态规划中，这种关系构成了“递推关系”或“状态转移方程”的基础。

**重叠子问题**是指在问题求解的过程中，许多子问题的解被重复计算。这是动态规划区别于分治算法的关键特征，也是动态规划引入“记忆化”（Memorization）或“表格法”（Tabulation）的原因。例如，在计算斐波那契数列时，许多子问题会被多次计算。

def fibonacci(n):
    if n <= 1:
        return n
    return fibonacci(n-1) + fibonacci(n-2)

以上Python代码是一个递归函数来计算斐波那契数列。它可以直观地表示出子问题的重叠性，如下图所示：

graph TD;
    A(fibon