揭秘GA算法的神秘面纱：入门指南，开启进化计算之旅

# 1. 遗传算法（GA）基础理论

遗传算法（GA）是一种受生物进化启发的优化算法。它模拟自然选择过程，通过不断迭代优化目标函数，寻找最优解。GA的基本原理包括：

- **编码：**将问题表示为染色体，染色体由基因组成，基因代表问题的不同特征。
- **初始化：**随机生成初始种群，种群中每个个体都是一个染色体。
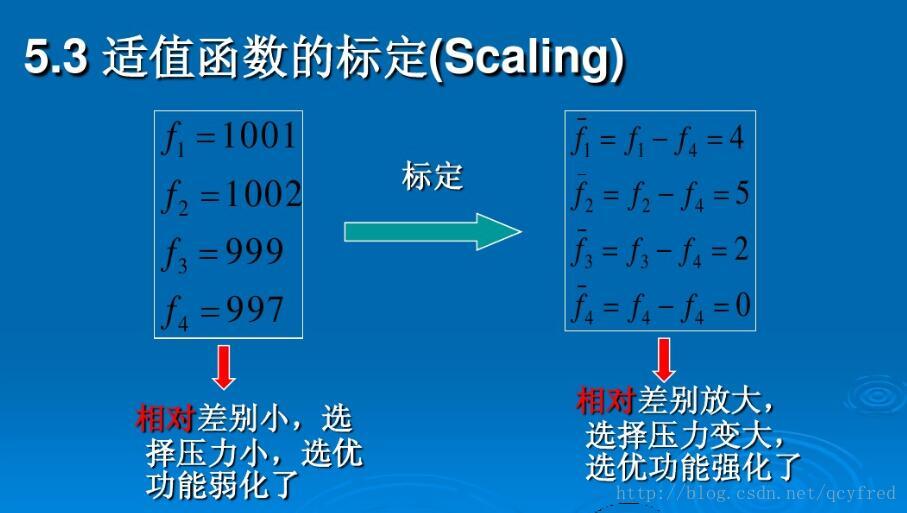
- **选择：**根据适应度函数选择种群中表现较好的个体，适应度函数衡量个体的优劣。
- **交叉：**将两个父代个体的基因交换，产生新的子代个体。
- **变异：**随机改变子代个体的基因，引入多样性。

# 2. GA编程技巧

遗传算法（GA）的编程技巧对于实现高效和有效的GA解决方案至关重要。本章节将深入探讨GA的编码、初始化、遗传操作、适应度函数和终止条件等关键方面。

### 2.1 GA的编码和初始化

#### 2.1.1 编码方式的选择

GA中，编码方式决定了如何将问题解决方案表示为染色体。常见的编码方式包括：

- **二进制编码：**将解决方案表示为一串0和1。
- **实数编码：**将解决方案表示为一组实数。
- **排列编码：**将解决方案表示为一个元素的排列。
- **树形编码：**将解决方案表示为一棵树。

编码方式的选择取决于问题类型和所需的精度。

#### 2.1.2 种群的初始化方法

种群初始化是指创建GA中初始种群的过程。常见的初始化方法包括：

- **随机初始化：**随机生成染色体。
- **贪婪初始化：**使用贪婪算法生成染色体。
- **启发式初始化：**使用领域知识生成染色体。

初始化方法的选择影响种群的多样性和GA的收敛速度。

### 2.2 GA的遗传操作

遗传操作是GA中模拟生物进化过程的关键步骤。它们包括：

#### 2.2.1 选择策略

选择策略决定了哪些染色体被选中进行繁殖。常见的策略包括：

- **轮盘赌选择：**根据适应度概率选择染色体。
- **锦标赛选择：**从随机选择的子集中选择最佳染色体。
- **精英选择：**保留种群中最好的染色体。

选择策略影响GA的收敛速度和多样性。

#### 2.2.2 交叉操作

交叉操作将两个父代染色体结合起来产生子代染色体。常见的交叉操作包括：

- **单点交叉：**在染色体上随机选择一个点，将父代染色体在该点处交叉。
- **多点交叉：**在染色体上随机选择多个点，将父代染色体在这些点处交叉。
- **均匀交叉：**逐位比较父代染色体，随机选择每个位来自哪个父代。

交叉操作增加种群的多样性，探索新的解决方案空间。

#### 2.2.3 变异操作

变异操作引入随机变化，防止GA陷入局部最优。常见的变异操作包括：

- **位翻转：**随机翻转染色体上的一个位。
- **插入：**在染色体中随机位置插入一个新值。
- **删除：**从染色体中随机位置删除一个值。

变异操作保持种群的多样性，避免算法过早收敛。

### 2.3 GA的适应度函数和终止条件

#### 2.3.1 适应度函数的设计原则

适应度函数衡量染色体的质量。设计适应度函数时应遵循以下原则：

- **明确性：**适应度函数应明确定义，易于计算。
- **相关性：**适应度函数应与问题的目标函数相关。
- **可区分性：**适应度函数应能够区分不同质量的染色体。

适应度函数的设计影响GA的收敛速度和找到最佳解决方案的能力。

#### 2.3.2 终止条件的设定

终止条件决定了GA何时停止运行。常见的终止条件包括：

- **最大迭代次数：**GA运行一定次数后停止。
- **收敛条件：**当种群达到一定程度的收敛时停止。
- **时间限制：**当GA运行超过一定时间时停止。

终止条件的选择取决于问题的复杂性和所需的精度。

# 3.1 GA求解优化问题

遗传算法在解决优化问题方面具有强大的能力，可以有效地处理复杂、非线性、多峰值等问题。

#### 3.1.1 连续优化问题

连续优化问题是指求解一个连续函数的极值问题。GA求解连续优化问题时，通常采用实数编码方式，将变量值直接映射到染色体上。

import numpy as np
import random

# 定义目标函数
def objective_function(x):
    return x**2 + 2*x + 3

# GA参数设置
pop_size = 100  # 种群规模
max_iter = 100  # 最大迭代次数
crossover_rate = 0.8  # 交叉率
mutation_rate = 0.1  # 变异率

# 种群初始化
population = np.random.uniform(-10, 10, (pop_size, 1))

# GA主循环
for i in range(max_iter):
    # 适应度计算
    fitness = np.apply_along_axis(objective_function, 1, population)

    # 选择
    parents = selection(population, fitness)

    # 交叉
    offspring = crossover(parents, crossover_rate)

    # 变异
    offspring = mutation(offspring, mutation_rate)

    # 更新种群
    population = offspring

# 输出最优解
best_solution = population[np.argmax(fitness)]
print("最优解：", best_solution)

**代码逻辑逐行解读：**

1. `objective_function` 定义了目标函数，需要最小化的函数。
2. `pop_size`、`max_iter`、`crossover_rate`、`mutation_rate` 设置了 GA 的参数。
3. `population` 初始化了种群，每个个体是一个实数。
4. 主循环遍历最大迭代次数。
5. `fitness` 计算每个个体的适应度，适应度越高表示个体越好。
6. `selection` 根据适应度选择父母个体。
7. `crossover` 根据交叉率进行交叉操作，产生新的后代。
8. `mutation` 根据变异率进行变异操作，产生新的后代。
9. `population` 更新种群，将新的后代加入种群。
10. `best_solution` 输出最优解，即适应度最高的个体。

#### 3.1.2 组合优化问题

组合优化问题是指求解一个离散函数的极值问题。GA求解组合优化问题时，通常采用二进制编码方式，将变量值映射到染色体上的二进制位上。

import random

# 定义目标函数
def objective_function(x):
    return -sum(x)

# GA参数设置
pop_size = 100  # 种群规模
max_iter = 100  # 最大迭代次数
crossover_rate = 0.8  # 交叉率
mutation_rate = 0.1  # 变异率

# 种群初始化
population = np.random.randint(2, size=(pop_size, 10))

# GA主循环
for i in range(max_iter):
    # 适应度计算
    fitness = np.apply_along_axis(objective_function, 1, population)

    # 选择
    parents = selection(population, fitness)

    # 交叉
    offspring = crossover(parents, crossover_rate)

    # 变异
    offspring = mutation(offspring, mutation_rate)

    # 更新种群
    population = offspring

# 输出最优解
best_solution = population[np.argmax(fitness)]
print("最优解：", best_solution)

**代码逻辑逐行解读：**

1. `objective_function` 定义了目标函数，需要最大化的函数。
2. `pop_size`、`max_iter`、`crossover_rate`、`mutation_rate` 设置了 GA 的参数。
3. `population` 初始化了种群，每个个体是一个二进制字符串。
4. 主循环遍历最大迭代次数。
5. `fitness` 计算每个个体的适应度，适应度越高表示个体越好。
6. `selection` 根据适应度选择父母个体。
7. `crossover` 根据交叉率进行交叉操作，产生新的后代。
8. `mutation` 根据变异率进行变异操作，产生新的后代。
9. `population` 更新种群，将新的后代加入种群。
10. `best_solution` 输出最优解，即适应度最高的个体。

# 4. GA进阶应用

### 4.1 GA的并行化

#### 4.1.1 并行化方法概述

遗传算法是一种迭代优化算法，其计算过程涉及大量种群个体的评估和更新。并行化GA可以有效提高算法的执行效率，尤其是在处理大型问题时。

并行化GA的主要方法包括：

- **个体并行化：**将种群中的个体分配到不同的处理器上并行评估，从而缩短评估时间。
- **操作并行化：**将遗传操作（选择、交叉、变异）并行执行，提高算法的迭代速度。
- **混合并行化：**结合个体并行化和操作并行化，实现更全面的并行化效果。

#### 4.1.2 并行化实现框架

并行化GA的实现框架通常包括以下组件：

- **主进程：**负责种群管理、遗传操作和终止条件判断。
- **从进程：**负责个体评估和更新。
- **通信机制：**用于主进程和从进程之间交换信息，如种群个体、评估结果等。

### 4.2 GA的杂交化

#### 4.2.1 GA与其他算法的结合

GA可以与其他算法结合，形成杂交算法，以增强算法的性能。常见的杂交算法包括：

- **GA-PSO：**将GA与粒子群优化（PSO）算法相结合，利用PSO的局部搜索能力增强GA的全局搜索能力。
- **GA-SA：**将GA与模拟退火（SA）算法相结合，利用SA的局部搜索能力提高GA的收敛精度。
- **GA-HC：**将GA与贪心算法（HC）相结合，利用HC的快速收敛能力加快GA的初始搜索过程。

#### 4.2.2 杂交化GA的应用实例

杂交化GA已成功应用于各种优化问题，例如：

- **旅行商问题：**GA-PSO算法在旅行商问题中表现出优异的求解性能，有效降低了路径长度。
- **函数优化：**GA-SA算法在函数优化问题中实现了高精度的求解，避免了陷入局部最优解。
- **调度优化：**GA-HC算法在调度优化问题中加快了算法的收敛速度，提高了调度效率。

### 4.3 GA的理论研究

#### 4.3.1 GA的收敛性分析

收敛性分析是研究GA是否能够收敛到最优解。常见的收敛性分析方法包括：

- **马尔可夫链分析：**将GA视为马尔可夫链，分析种群状态的转移概率，从而推导出收敛性条件。
- **模式识别分析：**将GA的搜索过程视为模式识别过程，分析种群中模式的演化规律，从而判断收敛性。
- **大偏差理论：**利用大偏差理论，分析GA在最优解附近区域的停留时间，从而推导出收敛性界限。

#### 4.3.2 GA的复杂度分析

复杂度分析是研究GA的计算时间和空间复杂度。常见的复杂度分析方法包括：

- **时间复杂度分析：**分析GA执行一次迭代所需的时间，包括种群评估、遗传操作和终止条件判断。
- **空间复杂度分析：**分析GA所需存储空间，包括种群个体、评估结果和中间变量。

通过复杂度分析，可以优化GA的算法参数和实现方式，以提高算法的效率和可扩展性。

# 5. GA展望与未来趋势

### 5.1 GA的最新发展和应用

近年来，GA在人工智能和生物信息学领域取得了显著进展。

**5.1.1 GA在人工智能领域的应用**

GA被广泛应用于人工智能领域，包括：

- **神经网络优化：**GA可以优化神经网络的权重和结构，提高其性能。
- **决策树优化：**GA可以优化决策树的结构和参数，提高其分类和回归精度。
- **强化学习：**GA可以优化强化学习算法中的奖励函数和策略，提高其学习效率。

**5.1.2 GA在生物信息学领域的应用**

GA在生物信息学领域也得到了广泛应用，包括：

- **基因序列分析：**GA可以用于分析基因序列，识别基因和预测蛋白质结构。
- **药物发现：**GA可以用于优化药物分子的结构和性质，提高其有效性和安全性。
- **生物信息学数据库搜索：**GA可以优化生物信息学数据库的搜索算法，提高搜索效率和准确性。

### 5.2 GA的未来发展方向

GA的未来发展方向主要包括：

**5.2.1 GA算法的改进和优化**

- **并行化和分布式GA：**利用并行计算和分布式计算技术提高GA的计算效率。
- **自适应GA：**开发自适应GA算法，自动调整GA参数以适应不同的问题。
- **混合GA：**将GA与其他优化算法相结合，形成混合GA算法，提高优化性能。

**5.2.2 GA在新领域的探索和应用**

- **大数据分析：**探索GA在处理和分析大数据方面的应用。
- **金融建模：**研究GA在金融建模和风险管理中的应用。
- **机器人学：**探索GA在机器人控制和规划中的应用。