GA算法实战指南：从零构建遗传算法模型，解锁优化新境界

# 1. 遗传算法（GA）概述

遗传算法（GA）是一种受自然进化启发的优化算法。它通过模拟生物进化过程，迭代地改进候选解决方案，以寻找最优解。

GA算法的核心思想是：

* **自然选择：**适应度较高的个体有更大的机会被选择繁殖。
* **遗传：**通过交叉和变异操作，产生新的个体，继承父母的特征。
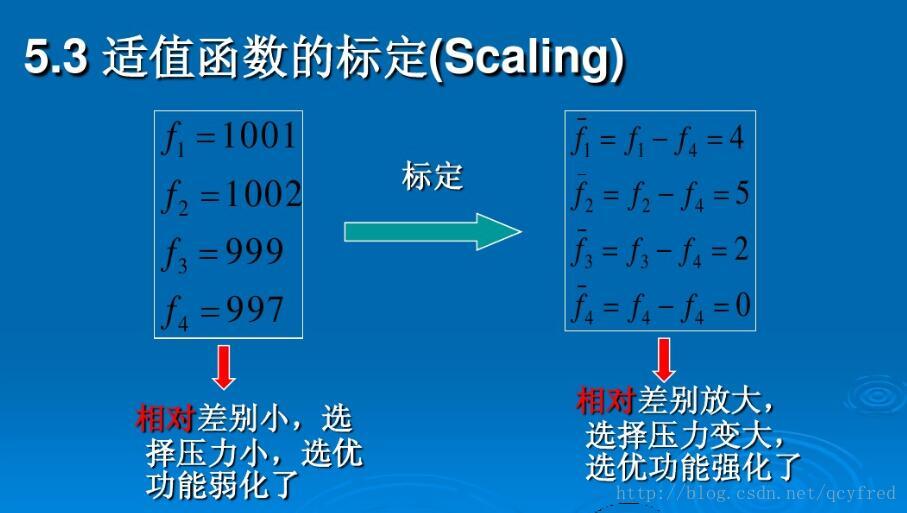
* **适应度函数：**衡量个体优劣的标准，用于指导选择过程。

GA算法具有以下优点：

* **鲁棒性：**不受初始解质量的影响，能够从不同的初始点找到最优解。
* **并行性：**可以并行执行，提高计算效率。
* **适用性：**可用于解决各种优化问题，包括离散和连续问题。

# 2. GA算法理论基础

### 2.1 GA算法的基本原理

#### 2.1.1 自然选择与遗传

遗传算法（GA）是一种受自然界进化论启发的优化算法。它模拟了生物进化过程中的自然选择和遗传机制。

在自然界中，个体拥有不同的基因型，这决定了它们的表型特征。表型特征决定了它们的适应度，即在特定环境中生存和繁殖的能力。适应度高的个体更有可能存活下来并繁衍后代，将它们的基因传递给下一代。

GA算法将问题解决方案编码为染色体，染色体由基因组成。每个基因代表问题的一个变量或特征。染色体的适应度由适应度函数决定，适应度函数衡量染色体解决方案的优劣。

#### 2.1.2 适应度函数与选择

适应度函数是GA算法的关键组成部分。它将染色体映射到一个实数值，该值表示染色体的适应度。适应度函数的设计取决于具体问题。

选择操作根据适应度对染色体进行选择。适应度高的染色体更有可能被选中，并与其他染色体进行交叉和变异操作。

### 2.2 GA算法的编码与解码

#### 2.2.1 二进制编码

二进制编码是GA算法中最常用的编码方式。它将染色体的基因表示为二进制数（0或1）。每个基因代表问题的一个变量或特征。

例如，对于一个求解旅行商问题的GA算法，染色体可能表示城市序列。每个基因代表一个城市，二进制数表示该城市在序列中的位置。

#### 2.2.2 实数编码

实数编码将染色体的基因表示为实数值。这对于具有连续变量的优化问题非常有用。

例如，对于一个优化神经网络超参数的GA算法，染色体可能表示神经网络的学习率和正则化参数。每个基因代表一个超参数，实数值表示该超参数的值。

#### 2.2.3 其他编码方式

除了二进制编码和实数编码外，还有其他编码方式可用于GA算法，包括：

* **置换编码：**用于排列问题，例如旅行商问题。
* **树编码：**用于表示树形结构，例如决策树。
* **图编码：**用于表示图结构，例如社交网络。

# 3.1 GA算法求解旅行商问题

#### 3.1.1 问题建模

旅行商问题（TSP）是一个经典的组合优化问题，描述如下：给定一组城市和它们之间的距离，求解一条最短的回路，使得该回路经过每个城市一次且仅一次。

TSP可以建模为一个图论问题，其中城市表示为图中的顶点，城市之间的距离表示为边的权重。GA算法求解TSP的编码方式通常采用顺序编码，即染色体表示为城市排列的顺序。

#### 3.1.2 GA算法求解过程

GA算法求解TSP的过程如下：

1. **初始化种群：**随机生成一组染色体，表示候选解。
2. **适应度计算：**计算每个染色体的适应度，即回路的总距离的倒数。
3. **选择：**根据适应度选择染色体进行繁殖，适应度高的染色体被选择的机会更大。
4. **交叉：**将两个父染色体进行交叉，产生新的子染色体。
5. **变异：**对子染色体进行变异，以引入多样性。
6. **重复步骤2-5：**直到满足终止条件（例如，达到最大迭代次数或找到足够好的解）。

import random
import math

# 城市坐标
cities = [(0, 0), (10, 0), (0, 10), (10, 10)]

# 距离计算
def distance(city1, city2):
    return math.sqrt((city1[0] - city2[0])**2 + (city1[1] - city2[1])**2)

# 适应度函数
def fitness(chromosome):
    total_distance = 0
    for i in range(len(chromosome)):
        total_distance += distance(chromosome[i], chromosome[(i+1)%len(chromosome)])
    return 1 / total_distance

# 选择操作
def selection(population, fitnesses):
    selected_chromosomes = []
    for _ in range(len(population)):
        # 轮盘赌选择
        selected_chromosome = random.choices(population, weights=fitnesses)[0]
        selected_chromosomes.append(selected_chromosome)
    return selected_chromosomes

# 交叉操作
def crossover(parent1, parent2):
    # 随机选择交叉点
    crossover_point = random.randint(1, len(parent1)-1)
    # 交换交叉点后的基因
    child1 = parent1[:crossover_point] + parent2[crossover_point:]
    child2 = parent2[:crossover_point] + parent1[crossover_point:]
    return child1, child2

# 变异操作
def mutation(chromosome):
    # 随机选择变异点
    mutation_point = random.randint(0, len(chromosome)-1)
    # 随机交换变异点处的基因
    chromosome[mutation_point], chromosome[random.randint(0, len(chromosome)-1)] = chromosome[random.randint(0, len(chromosome)-1)], chromosome[mutation_point]
    return chromosome

# GA算法主函数
def ga(population_size, num_generations):
    # 初始化种群
    population = [random.sample(cities, len(cities)) for _ in range(population_size)]
    # 初始化适应度
    fitnesses = [fitness(chromosome) for chromosome in population]

    for generation in range(num_generations):
        # 选择
        selected_chromosomes = selection(population, fitnesses)
        # 交叉
        new_population = []
        for i in range(0, len(selected_chromosomes), 2):
            child1, child2 = crossover(selected_chromosomes[i], selected_chromosomes[i+1])
            new_population.append(child1)
            new_population.append(child2)
        # 变异
        for chromosome in new_population:
            mutation(chromosome)
        # 计算新种群适应度
        new_fitnesses = [fitness(chromosome) for chromosome in new_population]
        # 更新种群
        population = new_population
        fitnesses = new_fitnesses

    # 返回最优解
    return population[fitnesses.index(max(fitnesses))]

# 4. GA算法进阶技术

### 4.1 GA算法的并行化

#### 4.1.1 并行化方法

GA算法的并行化是指将算法的不同部分分配到多个处理器或计算机上同时执行，以提高算法的效率。常见的并行化方法包括：

- **岛屿模型：**将种群划分为多个子种群，每个子种群在不同的处理器上进化。子种群之间定期交换个体，以保持种群多样性。
- **主从模型：**将种群划分为一个主种群和多个从种群。主种群负责生成新的个体，而从种群负责评估个体的适应度。
- **并行评估：**将种群中的个体分配到不同的处理器上，并行计算每个个体的适应度。

#### 4.1.2 并行化效果评估

GA算法并行化的效果可以通过以下指标来评估：

- **加速比：**并行算法与串行算法运行时间的比值。
- **效率：**并行算法中实际利用的处理器数量与总处理器数量的比值。
- **可扩展性：**并行算法在处理器数量增加时加速比的增长情况。

### 4.2 GA算法的杂交化

#### 4.2.1 杂交化策略

GA算法的杂交化是指将GA算法与其他优化算法或技术相结合，以提高算法的性能。常见的杂交化策略包括：

- **GA-PSO：**将GA算法与粒子群优化（PSO）算法相结合，利用PSO算法的快速收敛性来增强GA算法的全局搜索能力。
- **GA-SA：**将GA算法与模拟退火（SA）算法相结合，利用SA算法的局部搜索能力来优化GA算法的局部解。
- **GA-HC：**将GA算法与贪心算法（HC）相结合，利用HC算法的快速生成可行解的能力来提高GA算法的效率。

#### 4.2.2 杂交化效果分析

GA算法杂交化的效果可以通过以下指标来分析：

- **收敛速度：**杂交算法与纯GA算法收敛到最优解所需的时间。
- **解的质量：**杂交算法与纯GA算法找到的最优解的质量。
- **鲁棒性：**杂交算法在不同问题实例上的性能稳定性。

**代码示例：**

以下代码展示了GA算法并行化的一个简单实现：

import concurrent.futures

def evaluate_fitness(individual):
    # 计算个体的适应度
    return individual.fitness

def parallel_evaluate(population):
    with concurrent.futures.ThreadPoolExecutor() as executor:
        results = executor.map(evaluate_fitness, population)
    return list(results)

**流程图：**

以下流程图展示了GA算法并行化的岛屿模型：

graph LR
subgraph 主种群
    A[主种群]
end
subgraph 子种群1
    B[子种群1]
end
subgraph 子种群2
    C[子种群2]
end
subgraph 子种群3
    D[子种群3]
end
A --> B
A --> C
A --> D
B --> A
C --> A
D --> A

# 5.1 GA算法的工程实践

### 5.1.1 GA算法库和工具

在实际应用中，使用GA算法库和工具可以极大地简化算法的实现和部署。以下是一些流行的GA算法库：

- **DEAP (Distributed Evolutionary Algorithms in Python)**：一个Python库，提供了一系列GA算法的实现，包括选择、交叉、变异和进化策略。
- **PyGAD (Python Genetic Algorithm for Data)**：一个Python库，专为数据科学和机器学习任务而设计，提供了各种GA算法实现和实用功能。
- **jMetal (Java Metaheuristics Library)**：一个Java库，提供了广泛的元启发式算法，包括GA算法，具有并行化和分布式计算功能。
- **ECJ (Evolutionary Computation Java)**：一个Java库，提供了GA算法的全面实现，包括各种选择、交叉和变异算子。

### 5.1.2 GA算法性能优化

为了提高GA算法的性能，可以采用以下优化策略：

- **选择合适的编码方式**：选择与问题特征相匹配的编码方式可以提高搜索效率。
- **调整GA算法参数**：GA算法参数，如种群大小、选择压力和变异率，需要根据具体问题进行调整以获得最佳性能。
- **并行化GA算法**：通过将GA算法并行化到多个处理器或机器上，可以显著提高计算速度。
- **杂交化GA算法**：将GA算法与其他启发式算法或局部搜索方法相结合，可以提高搜索能力和收敛速度。