栈的应用案例：编译器语法分析，深入理解栈的应用

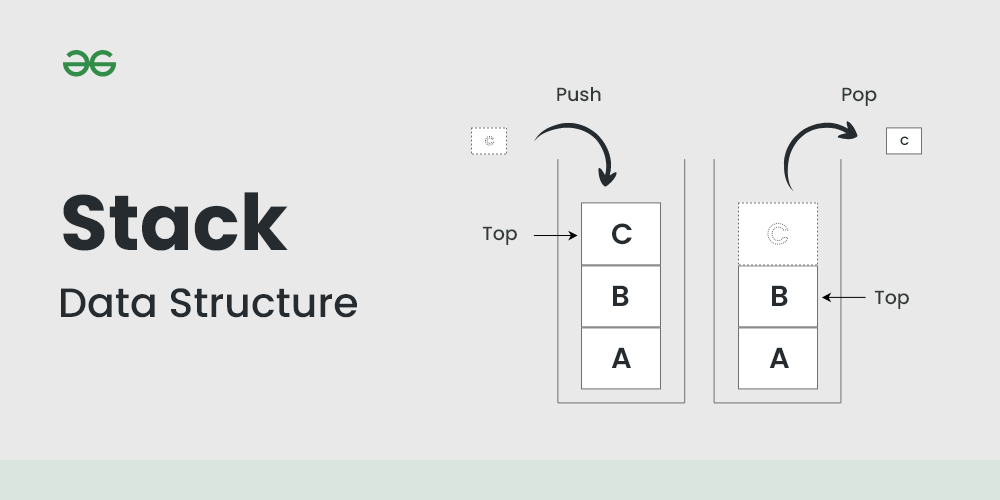
# 1. 栈的概念和基本操作**

栈是一种数据结构，它遵循后进先出 (LIFO) 的原则。这意味着最后添加的元素将首先被移除。栈的典型操作包括：

- **push(item)**：将一个元素添加到栈顶。
- **pop()**：从栈顶移除并返回一个元素。
- **peek()**：返回栈顶元素，但不移除它。
- **isEmpty()**：检查栈是否为空。

# 2. 栈在编译器语法分析中的应用

### 2.1 词法分析中的栈应用

#### 2.1.1 词法分析器简介

词法分析器是编译器的第一阶段，负责将源代码中的字符序列分解成有意义的词法单元（称为记号），例如标识符、关键字、运算符等。

#### 2.1.2 栈在词法分析中的作用

栈在词法分析中主要用于识别标识符和关键字。当词法分析器遇到一个字符序列时，它会将其压入栈中。然后，它会根据栈中字符序列的组合来判断当前字符序列是否为一个标识符或关键字。

例如，当词法分析器遇到字符序列 "int" 时，它会将其压入栈中。然后，它会检查栈顶字符是否为 "t"。如果是，则它会将 "t" 弹出栈并压入 "int"。接下来，它会检查栈顶字符是否为 "n"。如果是，则它会将 "n" 弹出栈并压入 "int"。最后，它会检查栈顶字符是否为 "i"。如果是，则它会将 "i" 弹出栈并压入 "int"。此时，栈中只剩下 "int"，表明该字符序列是一个标识符。

### 2.2 语法分析中的栈应用

#### 2.2.1 语法分析器简介

语法分析器是编译器的第二阶段，负责检查词法分析器生成的记号序列是否符合语法规则。

#### 2.2.2 栈在语法分析中的作用

栈在语法分析中主要用于构造语法树。当语法分析器遇到一个语法规则时，它会将该语法规则的左部压入栈中。然后，它会根据栈中语法规则左部的组合来判断当前记号序列是否符合该语法规则。

例如，当语法分析器遇到语法规则 "E -> T + E" 时，它会将 "E" 压入栈中。然后，它会检查栈顶语法规则左部是否为 "E"。如果是，则它会将 "E" 弹出栈并压入 "T + E"。接下来，它会检查栈顶语法规则左部是否为 "T"。如果是，则它会将 "T" 弹出栈并压入 "T + E"。最后，它会检查栈顶语法规则左部是否为 "+"。如果是，则它会将 "+" 弹出栈并压入 "T + E"。此时，栈中只剩下 "T + E"，表明该记号序列符合语法规则 "E -> T + E"。

# 3.1 函数调用和递归

#### 3.1.1 函数调用过程中的栈操作

当一个函数被调用时，系统会为该函数创建一个新的栈帧。栈帧包含了该函数的局部变量、参数和返回地址。当函数执行完毕时，其栈帧会被销毁。

**代码块：**

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

**逻辑分析：**

该代码块实现了阶乘函数。当调用`factorial(n)`时，系统会为其创建一个栈帧，其中包含参数`n`。如果`n`为0，则函数直接返回1。否则，函数会递归调用`factorial(n-1)`，并将其结果与`n`相乘。递归调用会继续进行，直到`n`变为0。此时，栈帧会被逐个销毁，并最终返回阶乘结果。

#### 3.1.2 递归函数中的栈操作

递归函数是一种调用自身的一种函数。在递归调用过程中，系统会为每次调用创建一个新的栈帧。

**代码块：**

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

**逻辑分析：**

该代码块实现了斐波那契数列函数。当调用`fibonacci(n)`时，系统会为其创建一个栈帧，其中包含参数`n`。如果`n`小于等于1，则函数直接返回`n`。否则，函数会递归调用`fibonacci(n-1)`和`fibonacci(n-2)`，并将结果相加。递归调用会继续进行，直到`n`变为0或1。此时，栈帧会被逐个销毁，并最终返回斐波那契数。

### 3.2 表达式求值

#### 3.2.1 中缀表达式求值中的栈应用

中缀表达式是一种数学表达式，其中运算符位于操作数之间。例如，表达式`1 + 2 * 3`是一个中缀表达式。

**代码块：**

def evaluate_infix(expression):
    stack = []
    for token in expression.split():
        if token in "+-*/":
            op2 = stack.pop()
            op1 = stack.pop()
            result = eval(op1 + token + op2)
            stack.append(result)
        else:
            stack.append(token)
    return stack[0]

**逻辑分析：**

该代码块实现了中缀表达式求值函数。它使用一个栈来存储操作数和运算符。当遇到一个操作数时，将其压入栈中。当遇到一个运算符时，从栈中弹出两个操作数，执行运算，并将结果压入栈中。最后，栈中剩下的元素就是表达式的值。

#### 3.2.2 后缀表达式求值中的栈应用

后缀表达式是一种数学表达式，其中运算符位于操作数之后。例如，表达式`1 2 3 * +`是一个后缀表达式。

**代码块：**

def evaluate_postfix(expression):
    stack = []
    for token in expression.split():
        if token not in "+-*/":
            stack.append(int(token))
        else:
            op2 = stack.pop()
            op1 = stack.pop()
            result = eval(op1 + token + op2)
            stack.append(result)
    return stack[0]

**逻辑分析：**

该代码块实现了后缀表达式求值函数。它使用一个栈来存储操作数。当遇到一个操作数时，将其压入栈中。当遇到一个运算符时，从栈中弹出两个操作数，执行运算，并将结果压入栈中。最后，栈中剩下的元素就是表达式的值。

# 4. 栈的实现与优化

### 4.1 栈的数组实现

#### 4.1.1 数组栈的结构和操作

数组栈是一种使用数组来存储元素的栈实现。它使用一个称为栈顶指针（top）的变量来跟踪栈顶元素的位置。

class ArrayStack:
    def __init__(self, size):
        self.stack = [None] * size
        self.top = -1

    def push(self, element):
        if self.top == len(self.stack) - 1: