【回溯算法】：解决复杂问题的10个典型问题剖析


# 摘要
回溯算法是一种用于解决组合优化问题的算法，它通过递归遍历可能的候选解来寻找问题的解，若发现当前候选解不可能达到最优解，则回溯到上一步选择其他路径。本文从理论基础到实现原理，再到经典问题的解决方法，系统地探讨了回溯算法。文章详细介绍了算法的基本概念、关键技术，如状态空间树的构建和剪枝策略，以及对算法时间复杂度的分析。随后，本文列举了回溯算法在现代编程中的多个应用实例，包括组合、排列问题及NP完全问题的近似解。文章最后探讨了回溯算法的优化技巧和面临的挑战，以及其在人工智能领域的应用前景和理论创新的可能性。

# 关键字
回溯算法；理论基础；状态空间树；剪枝策略；时间复杂度；NP完全问题

参考资源链接：[数据结构习题集：1800题详解+高校试题&答案](https://wenku.csdn.net/doc/37zekj7s6j?spm=1055.2635.3001.10343)
# 1. 回溯算法的理论基础

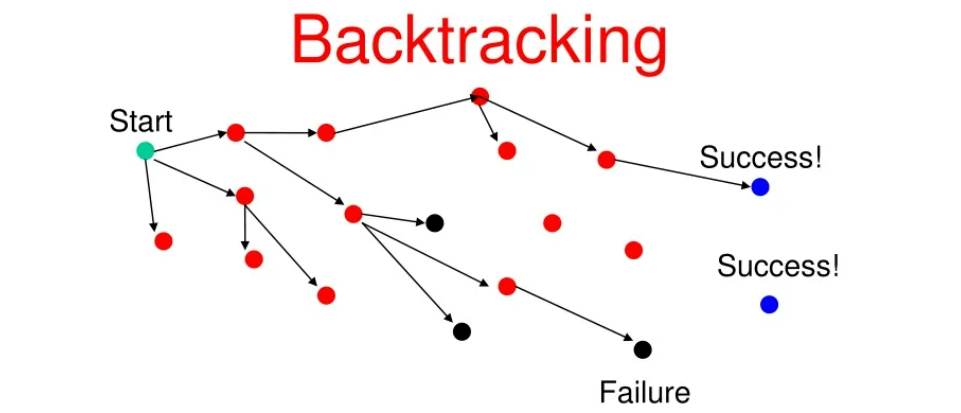
回溯算法是解决组合问题的一类重要算法，它通过递归地构建潜在解，并在发现当前解不可行时回退，探索其他可能的解。这种算法的核心思想是尝试与回溯，即它尝试构建解的每一种可能情况，并在出现错误时返回至上一步，然后继续尝试其他路径。

## 1.1 回溯算法的基本思想

回溯算法最显著的特点是“试错”。在构建问题解的过程中，算法会遍历决策树的所有节点，当遇到不满足约束条件的解时，会撤销上一步或几步的决定，即回溯到上一个节点，并在该节点选择新的选项进行尝试。

## 1.2 算法的应用领域

回溯算法广泛应用于各类组合问题，如八皇后问题、图的着色问题、旅行商问题（TSP）等。这些问题通常具有一个共同特点：解空间庞大，且解的数量随着问题规模的增加呈指数增长，需要有效的算法来搜索解空间。

了解回溯算法的基本概念和理论是进一步掌握其实现原理和应用实践的基础。在后续的章节中，我们将详细探讨回溯算法的实现细节和解决经典问题的实际应用。

# 2. 回溯算法的实现原理

## 2.1 回溯算法的基本概念

### 2.1.1 定义与应用领域

回溯算法是一种通过探索所有可能情况来找出所有解的算法，如果发现已不满足求解条件，则回退到上一步，将该点的状态改变后再继续尝试寻找。回溯算法在人工智能领域尤为关键，如路径查找、游戏树的搜索、逻辑推理问题以及约束满足问题中广泛应用。

### 2.1.2 算法结构与流程

回溯算法的结构可以分为两个主要部分：递归结构和回溯结构。递归结构用于在搜索过程中深入每一层可能性，而回溯结构则用于当发现当前路径不可能导致解时，回退到上一层并尝试其他可能性。其基本流程包括：开始时初始化数据结构，然后开始递归搜索，对于每一个可能的选项，检查是否满足约束条件，如果不满足就回溯；如果满足则继续搜索，直到找到解或者所有选项都尝试完毕。

## 2.2 回溯算法的关键技术

### 2.2.1 状态空间树的构建

状态空间树是一种用来描述回溯搜索过程的树形结构，每个节点代表问题状态，边表示状态转换。为了构建状态空间树，通常需要定义一个起始状态作为根节点，并且为每一种可能的操作定义一个转换规则。在构建状态空间树时，需要保证树的每一个分支都代表了一种可能的解决方案路径。

graph TD
    A[根节点] -->|选择方案1| B(节点1)
    A -->|选择方案2| C(节点2)
    B -->|进一步选择| D(节点1.1)
    B -->|进一步选择| E(节点1.2)
    C -->|进一步选择| F(节点2.1)
    C -->|进一步选择| G(节点2.2)

### 2.2.2 剪枝策略的运用

剪枝策略是优化回溯算法性能的重要手段，其基本思想是在搜索过程中，尽早地放弃不可能产生解的路径。剪枝可以通过设置条件判断来实现，例如：当一个部分解已经不满足问题的某些约束时，可以停止对其进行进一步展开。合理的剪枝策略可以显著减少搜索空间，提升算法效率。

## 2.3 回溯算法的时间复杂度分析

### 2.3.1 算法复杂度计算方法

回溯算法的时间复杂度通常取决于状态空间树的大小，它与问题的规模以及问题的限制条件紧密相关。在最坏的情况下，回溯算法可能需要遍历整个状态空间树，其时间复杂度为 O(n!)，其中 n 为状态空间树的节点数量。然而，通过合理的剪枝策略，往往可以将时间复杂度降低到多项式级别。

### 2.3.2 实例分析：N皇后问题

N 皇后问题是一个典型的回溯算法问题，要求在一个 n×n 的棋盘上放置 n 个皇后，使得它们互不攻击，即任意两个皇后都不在同一行、同一列或同一对角线上。其状态空间树非常庞大，但通过剪枝可以有效减少搜索量。

以 4 皇后问题为例，状态空间树的根节点代表棋盘上没有皇后的情况，第一层代表第一行皇后的所有可能位置，第二层代表第二行的可能位置，以此类推。当放置皇后的过程中发现冲突，就进行回溯，尝试其他可能位置。通过剪枝，通常在达到树的三层或四层时，就能找到所有解或确定无解。

// 4皇后问题的递归回溯函数伪代码
function solveNQueens(board, row, n):
    if row == n:
        addSolution(board)
        return
    for col in range(n):
        if isSafe(board, row, col, n):
            placeQueen(board, row, col, n)
            solveNQueens(board, row + 1, n)
            removeQueen(board, row, col, n)

在上面的伪代码中，`isSafe` 函数用来判断当前位置是否安全，`placeQueen` 和 `removeQueen` 分别用来放置和移除皇后，`addSolution` 用来输出当前找到的一个解决方案。

通过这个实例分析，可以更深入地理解回溯算法的工作原理以及剪枝策略的应用。接下来，让我们探索回溯算法是如何解决其他经典问题的。

# 3. ```
# 第三章：回溯算法解决经典问题

回溯算法通过系统地尝试问题的每一种可能，并通过剪枝技术剔除不可能的选项来解决问题。在本章节中，我们将探索回溯算法在解决几个经典问题中的应用。

## 3.1 八皇后问题

### 3.1.1 问题描述与规则

八皇后问题是一个经典的回溯算法应用实例，目标是在8×8的棋盘上放置八个皇后，使得它们互不攻击。所谓“攻击”是指任意两个皇后处在同一行、同一列或同一对角线上。问题的解决需要找出所有可能的布局。

### 3.1.2 解决方案的实现与优化

实现八皇后问题的回溯算法，需要定义棋盘、尝试放置皇后并检查条件是否满足、回溯到上一状态进行调整。下面是一个简化的Python实现方案：

def is_safe(board, row, col):
    # 检查同列是否有皇后互相冲突
    for i in range(row):
        if board[i] == col or \
           board[i] - i == col - row or \
           board[i] + i == col + row:
            return False
    return True

def solve_queens(board, row):
    if row >= len(board):
        # 所有皇后都放置好，打印解决方案
        print([board[i] for i in range(len(board))])
        return True
    for col in range(len(board)):
        if is_safe(board, row, col):
            board[row] = col
            solve_queens(board, row + 1)
            # 不需要显式回溯，因为Python列表是可变对象
    return False  # 如果没有解决方案，则回溯

def eight_queens():
    board = [-1] * 8  # 初始化棋盘
    solve_queens(board, 0)

eight_queens()

在优化方面，可以考虑位运算优化检查冲突步骤，例如使用位掩码来加速判断皇后之间是否相互攻击。

## 3.2 图的着色问题

### 3.2.1 问题描述与应用场景

图的着色问题要求将一个无向图的每个顶点着上颜色，使得相邻的顶点颜色不同，且使用的颜色数量尽可能少。这个问题在许多领域有广泛的应用，如频率分配、时间表安排等。

### 3.2.2 回溯算法的应用实例

一个简单的应用实例是4个区域的着色问题，使用回溯算法来寻找最少颜色数的解决方案：

def is_safe_color(graph, colors, v, c):
    # 检查顶点v着色c是否安全
    for i in range(len(graph)):
        if graph[v][i] and c == colors[i]:
            return False
    return True

def graph_coloring(graph, colors, v, n):
    # 如果顶点v是最后一个顶点，则找到了解决方案
    if v == n:
        return True
    # 尝试不同的颜色
    for c in range(1, n + 1):
        if is_safe_color(graph, colors, v, c):
            colors[v] = c
            if graph_coloring(graph, colors, v + 1, n):
                return True
            # 回溯步骤
            colors[v] = 0
    return False

def graph_coloring_example():
    graph = [[0, 1, 1, 1],
             [1, 0, 1, 0],
             [1, 1, 0, 1],
             [1, 0, 1, 0]]
    n = len(graph)
    colors = [0] * n
    if graph_coloring(graph, colors, 0, n):
        print("Solution exists: ", colors)
    else:
        print("Solution does not exist")

graph_coloring_example()

这个问题也可以通过启发式算法进行优化，例如贪婪算法，它可以在合理的时间内找到一个接近最优的解决方案。

## 3.3 子集和问题

### 3.3.1 问题定义及解空间

子集和问题是指给定一个集合S和一个数sum，判断S中是否存在一个子集的和等于sum。这个问题的解空间是指数级的，因为需要考虑S的每个可能子集。

### 3.3.2 算法实现与优化技巧

实现子集和问题的回溯算法，关键在于递归地探索所有可能的子集，并检查其和是否满足条件。优化技巧包括记忆化搜索，即存储已经计算过的结果，避免重复计算。

def is_subset_sum(set, n, sum):
    # 创建一个二维数组来存储子问题的解
    dp = [[False for _ in range(sum + 1)] for _ in range(n + 1)]

    # 如果和为0，则子集为空是唯一的解
    for i in range(n + 1):
        dp[i][0] = True

    # 填充dp数组
    for i in range(1, n + 1):
        for j in range(1, sum + 1):
            if j < set[i - 1]:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = dp[i - 1][j] or dp[i - 1][j - set[i - 1]]
    return dp[n]