回溯算法入门：解决复杂问题的递归策略，专家级指导

# 1. 回溯算法概述与应用

回溯算法是一种通过探索所有可能情况来解决问题的算法，它具有“试错”的特点，常用于需要穷举所有可能性的场景。在这一章节中，我们将概述回溯算法的基本概念，以及它在现实世界中的应用。

## 1.1 回溯算法的定义与应用概述

回溯算法的核心在于通过递归的方式，在每一步选择中尝试每一个可能的选项，如果发现当前选择不可能到达最终解，则撤销当前选择，返回到上一步重新选择。它的优势在于能够解决诸如组合、排列以及约束满足等复杂问题。在实际应用中，回溯算法被广泛用于数独、八皇后、图的着色以及旅行商问题等经典问题中。

## 1.2 回溯算法的工作原理

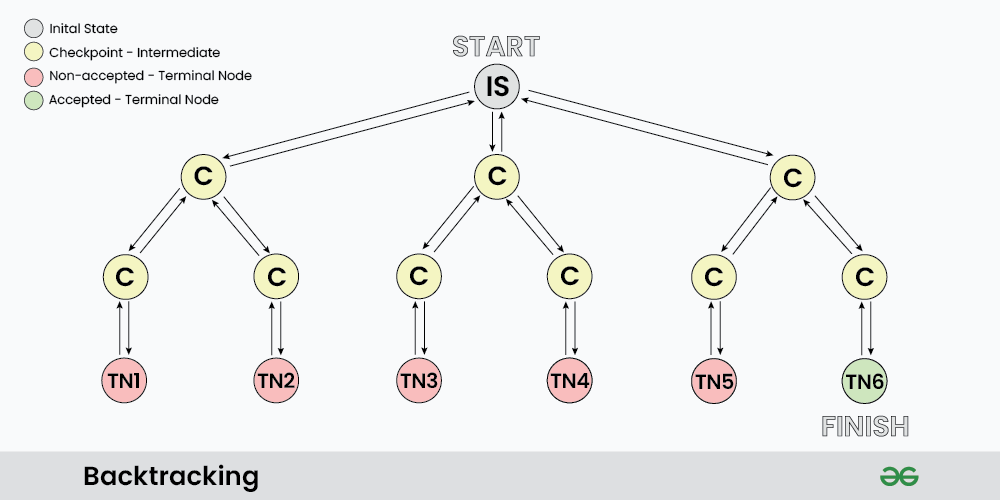
回溯算法利用解空间树来表示所有可能的解空间，并通过深度优先搜索(DFS)来遍历这棵树。在搜索过程中，算法会剪枝以避免无效搜索，从而提高搜索效率。每到达树的一个节点，算法都会尝试一个可能的路径，如果这个路径不能达到有效解，算法则会返回到上一个节点，并尝试其他的路径。这种回溯机制是算法名称的由来。

## 1.3 回溯算法的应用领域

回溯算法由于其强大的穷举能力，在多个领域都有应用。例如，在人工智能中，它被用来搜索和优化决策树；在密码学中，用于破解密码；在调度问题中，寻找最优的任务分配。此外，在日常生活中，如路径规划、网络游戏的AI行为设计等，回溯算法都扮演着重要角色。

回溯算法作为一种基础且强大的算法框架，对于解决特定类型的问题具有不可替代的作用。在本章后续部分，我们将深入探讨回溯算法的理论基础，并通过具体案例演示其实现方法和应用技巧。

# 2. 回溯算法基础理论

### 2.1 回溯算法的定义与原理

#### 2.1.1 算法定义与关键特征
回溯算法是一种系统地搜索问题答案的算法，它采用试错的方法，通过递归的方式，构建解空间树，对各种可能的情况进行尝试。关键特征之一是它能够暂时保存当前状态，一旦发现当前尝试的路径不能得到有效的解决方案，就会回退到上一状态，尝试其他路径。

回溯算法的关键特征可以概括为以下几点：

- **递归结构**：回溯算法通常使用递归函数来遍历解空间。
- **回溯操作**：算法通过回溯操作回到上一个决策点，重新尝试不同的路径。
- **剪枝操作**：在搜索过程中，剪枝可以减少无效搜索，提高算法效率。
- **完整性保证**：回溯算法能够遍历所有可能的解空间，保证找到所有解或确定不存在解。

#### 2.1.2 解空间树的概念与构建
解空间树是一种用来表示所有可能解的数据结构，通常以树的形式构建。树的每个节点代表问题的一个状态，节点的边代表决策或选择。构建解空间树的步骤包括：

1. **定义根节点**：根节点代表问题的初始状态。
2. **分支生成**：为根节点生成所有可能的子节点，每个子节点代表一种选择的结果。
3. **递归分支**：对每个子节点继续进行分支生成，直至达到终止条件。
4. **终止条件定义**：定义何时停止分支生成，例如到达问题的解，或者没有可行的后续选择。

解空间树通常在内存中构建，且以隐式方式存在。在实际编程中，我们不会显式地构建整个树，而是通过递归函数模拟这一过程。

### 2.2 回溯算法的搜索策略

#### 2.2.1 深度优先搜索(DFS)基础
深度优先搜索（DFS）是回溯算法的核心搜索策略。DFS 通过尽可能深地搜索解空间树的分支来寻找问题的解，当当前分支无法进一步深入时，便回溯到上一节点，尝试其他分支。

实现 DFS 的基本步骤如下：

1. **访问起始节点**：开始搜索，访问起始节点。
2. **生成子节点**：对于当前节点，生成所有可能的子节点。
3. **选择节点**：从子节点中选择一个进行进一步的搜索。
4. **重复步骤 2 和 3**：对所选择的子节点重复步骤 2 和 3，直到达到解或子节点为空。
5. **回溯**：如果当前节点没有可探索的子节点，则回溯到上一个节点，并尝试其他子节点。

#### 2.2.2 剪枝策略的基本概念
剪枝是回溯算法中用于提高效率的一个重要概念。它通过在搜索过程中跳过那些不可能产生有效解的节点来减少搜索空间。剪枝策略可以减少不必要的计算，提高算法的执行效率。

剪枝策略的实现方式有多种，包括但不限于：

- **约束传播**：利用问题的约束条件来减少选择。
- **最优性剪枝**：如果当前路径已不可能产生最优解，就剪掉当前路径。
- **可行性剪枝**：如果当前路径无法满足问题的约束条件，则剪枝。

### 2.3 回溯算法的伪代码与模板

#### 2.3.1 标准回溯算法的伪代码分析
回溯算法的伪代码通常包含以下几个部分：

function backtrack(路径, 选择列表):
    if 满足结束条件:
        结果.append(路径)
        return
    for 选择 in 选择列表:
        做出选择
        if 有效(路径, 选择):
            backtrack(路径, 选择列表)
        撤销选择

在这段伪代码中：

- `路径`：表示从根节点到当前节点的路径。
- `选择列表`：当前节点可能的选择。
- `结束条件`：确定是否达到解或者没有可尝试的选择。
- `有效(路径, 选择)`：判断当前的选择是否满足问题的约束条件。

#### 2.3.2 回溯模板的实际应用
实际应用回溯模板时，需要根据具体问题调整选择列表的生成和有效性的判断。以下是一个基于回溯模板解决 8 皇后问题的伪代码：

function solveNQueens(棋盘大小 n):
    棋盘 = 初始化大小为 n*n 的棋盘
    结果 = []
    function backtrack(行, 对角线1, 对角线2):
        if 行 == n:
            结果.append(棋盘)
            return
        for 列 in range(n):
            if isSafe(行, 列, 对角线1, 对角线2):
                棋盘[行][列] = 'Q'
                backtrack(行 + 1, 对角线1 + 列, 对角线2 + (n - 列 - 1))
                棋盘[行][列] = '.'  // 撤销选择
    backtrack(0, 0, 0)
    return 结果

在这个模板中，对角线1和对角线2是通过索引对称性的限制来避免重复状态的尝试。`isSafe` 函数用于检查放置皇后是否会导致冲突。如果条件满足，则放置皇后，并递归调用 `backtrack` 函数；否则撤销皇后放置，尝试其他位置。

通过上述伪代码，我们可以看到回溯模板的结构清晰，易于理解和实现。通过调整选择列表和有效性的判断，回溯模板能够解决各种不同的问题，展示出极强的通用性和灵活性。

# 3. 回溯算法的实现技巧

## 3.1 变量与数据结构的选择

### 3.1.1 变量的作用域和生命周期

在实现回溯算法时，合理选择变量的作用域和生命周期是至关重要的。变量的作用域决定了变量在哪里可以被访问，而生命周期则定义了变量从创建到销毁的过程。理解这两点有助于我们更好地管理内存和状态，以及提高代码的可读性和效率。

通常，在回溯算法中，我们会使用全局变量来存储一些固定的信息，例如问题的规模和目标状态，以及一些控制搜索行为的参数。而局部变量则用于存储临时数据和递归过程中的中间状态。局部变量的生命周期仅限于其所在的函数调用栈，当递归函数返回时，局部变量就会被销毁。

### 3.1.2 选择合适的数据结构存储状态

存储状态是回溯算法设计的关键一环。选择合适的数据结构能够有效提升算法的性能和可扩展性。常见的选择包括数组、列表、字典等。对于回溯算法，我们常常使用数组或列表来表示问题的候选解，并根据问题的特性采用不同的数据结构。

例如，在解决N皇后问题时，我们可以使用一维数组来表示棋盘上每一行皇后的放置情况，数组的索引代表行号，数组值表示皇后在该行的列号。这种表示方法简洁明了，易于实现和理解。

## 3.2 状态的保存与恢复

### 3.2.1 状态保存的时机与方法

在回溯算法中，状态的保存通常发生在递归函数的开始阶段。当进入一个新的搜索分支时，我们需要保存当前节点的状态，以便于后续可能的回溯操作。通常，我们会将这些状态保存到一个栈结构中，或者是临时变量中。

例如，在一个N皇后问题的实现中，当我们放置一个新的皇后时，我们需要保存当前行的信息以及之前行的皇后位置。这可以通过简单地将当前行和之前行的皇后位置数组加入到一个栈结构中来完成。

### 3.2.2 状态恢复的技术细节

与状态保存相对应的是状态恢复。状态恢复发生在回溯过程中，即当我们在当前分支中无法找到解时，需要回退到上一个状态，恢复之前保存的状态，并继续尝试其他的搜索分支。

在技术实现上，状态恢复通常是通过弹出之前保存的状态信息来完成的。这个过程需要确保恢复的状态与当前搜索深度完全一致，否则可能会导致算法逻辑错误，甚至在极端情况下出现无限循环。

## 3.3 递归函数的设计原则

### 3.3.1 递归函数的结构设计

回溯算法天然适合使用递归函数来实现。递归函数的设计需要遵循几个基本原则，以确保算法的正确性和效率。

首先，递归函数需要有明确的递归终止条件，这是递归逻辑能够结束的基础。其次，每次递归调用都应该缩小问题规模，这样才能够保证递归能够逐步逼近问题的解决方案。最后，需要合理设计递归函数的参数，确保每个递归层次都能够正确地传递和更新状态信息。

### 3.3.2 递归终止条件的确定

递归终止条件是回溯算法设计中最关键的部分之一。终止条件的确定通常依赖于问题的具体需求和约束条件。在回溯算法中，我们通常根据是否找到了一个满足所有约束条件的解，或者是搜索到了