二叉搜索树深入解析与平衡操作:保持树平衡的6大技巧
发布时间: 2024-09-09 21:34:19 阅读量: 40 订阅数: 39 


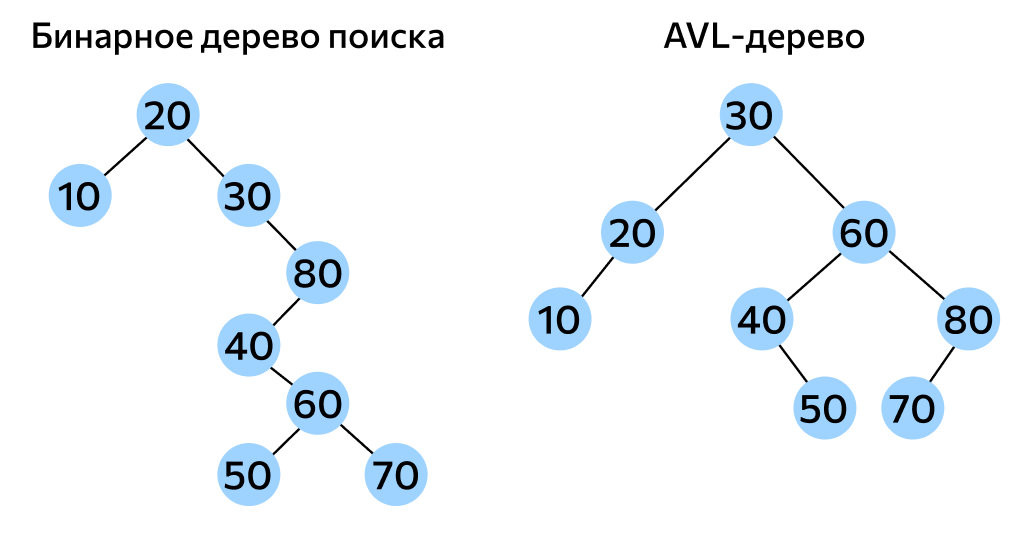
广东工业大学数据结构课程设计-平衡二叉树的演示
# 1. 二叉搜索树的基础知识
## 1.1 二叉搜索树定义
二叉搜索树(Binary Search Tree, BST),也称为二叉查找树或二叉排序树,是一种特殊的二叉树。对于树中的每一个节点,其左子树上的所有元素的值都小于当前节点的值,其右子树上的所有元素的值都大于当前节点的值。这种特性决定了二叉搜索树的中序遍历可以得到一个递增的序列。
## 1.2 树的结构特点
在二叉搜索树中,节点的插入、查找和删除操作都利用了树的排序特性,使得这些操作的时间复杂度可以达到对数级别,即O(log n),这在处理大量数据时具有显著的性能优势。
## 1.3 二叉搜索树的应用场景
二叉搜索树广泛应用于各种需要快速查找、排序和更新数据的场合。例如,数据库索引结构、优先队列的实现以及编程语言中的映射和集合数据结构等。
```mermaid
graph TD;
A((BST)) -->|每个节点| B((左子树<br>val < node.val))
A --> C((右子树<br>val > node.val))
```
以上图示简单展示了二叉搜索树的结构特点,左边的子树节点值都小于根节点,右边的子树节点值都大于根节点。
# 2. 二叉树的遍历算法
## 2.1 二叉树遍历理论
### 2.1.1 前序遍历的原理与应用
前序遍历是二叉树遍历中的基础算法之一,其核心思想是先访问根节点,然后递归地进行左子树的前序遍历,最后递归地进行右子树的前序遍历。前序遍历的这种“根-左-右”的顺序使得我们能够按照一定的顺序处理树中的每一个节点。
在应用中,前序遍历常用于以下场景:
- 复制二叉树:因为根节点首先被访问,这使得我们可以创建一个新的树节点,并以相同的顺序复制左右子树。
- 检查二叉树的结构:通过前序遍历,我们可以确定树的结构,因为它按照特定的顺序访问所有节点。
### 2.1.2 中序遍历的原理与应用
中序遍历遍历树的顺序是“左-根-右”,这使得在访问根节点之前,我们可以访问其所有的左子节点。中序遍历的特点是,对于二叉搜索树来说,它会按照节点值的升序输出所有节点。这一特性使得中序遍历在处理排序数据时非常有用。
中序遍历的典型应用场景包括:
- 输出有序数据:如二叉搜索树中的节点值排序。
- 检查二叉树的排序正确性:通过中序遍历,我们可以验证二叉树是否为二叉搜索树。
### 2.1.3 后序遍历的原理与应用
后序遍历是按照“左-右-根”的顺序进行的。这意味着每个节点只有在它的两个子树被访问之后才会被访问。后序遍历的特点是它允许在访问根节点之前处理所有的子节点,这使得它在某些情况下非常有用,比如删除一棵树。
后序遍历的应用场景如下:
- 删除二叉树:可以确保在删除根节点之前子节点已被正确删除。
- 计算树的大小或深度:通过后序遍历可以累积子树的信息来计算整个树的大小或深度。
## 2.2 遍历算法的实践实现
### 2.2.1 迭代法实现遍历
迭代法使用栈来模拟递归过程,避免了递归可能造成的栈溢出。以下是使用Python实现的前序遍历的迭代法代码:
```python
def preorderTraversal(root):
stack, output = [root], []
while stack:
node = stack.pop()
if node:
output.append(node.val)
stack.append(node.right) # 先右后左,保证左子树先于右子树被访问
stack.append(node.left)
return output
```
在这段代码中,我们首先将根节点压入栈中,然后不断循环直到栈为空。每次循环中,我们取出栈顶元素并将其值加入输出列表,然后先将右子节点压入栈中(如果存在),最后将左子节点压入栈中。这样确保了左子树比右子树更早被处理。
### 2.2.2 递归法实现遍历
递归法是利用函数自身的调用来实现树的遍历,它直观并且易于理解。以下是使用Python实现的中序遍历的递归法代码:
```python
def inorderTraversal(root):
return inorderTraversal(root.left) + [root.val] + inorderTraversal(root.right) if root else []
```
这段递归函数的工作原理是:如果当前节点为空,则返回空列表;否则,递归遍历左子树,将当前节点的值加入列表,递归遍历右子树。通过这种方式,我们按照“左-根-右”的顺序访问了树中的所有节点。
### 2.2.3 非递归的中序遍历
非递归的中序遍历需要借助一个栈来实现,我们从根节点开始,不断地将其所有左子节点压入栈中。当无法继续向左时,开始从栈中弹出节点并访问,然后转向该节点的右子树,重复这一过程。以下是实现的代码:
```python
def inorderTraversal(root):
stack, output = [], []
while root or stack:
while root:
stack.append(root)
root = root.left
root = stack.pop()
output.append(root.val)
root = root.right
return output
```
在这段代码中,我们首先创建一个空栈和空输出列表。然后开始一个循环,在循环中,我们将当前节点的所有左子节点压入栈中,然后访问当前节点,并转向其右子节点继续上述过程。这样,我们通过栈结构实现了中序遍历的顺序。
在下一节中,我们将讨论二叉搜索树的插入与删除操作,这些操作也是基于树的遍历算法。
# 3. 二叉搜索树的插入与删除操作
二叉搜索树(BST)的插入与删除是数据结构与算法中的基本操作,其性能直接影响到树的效率。在本章节中,我们将深入探讨插入与删除操作的原理与实践,以及在操作过程中遇到的边界情况。
## 3.1 插入操作的原理与实践
### 3.1.1 插入算法的基本逻辑
在二叉搜索树中插入一个新的节点时,首先需要遍历树以找到合适的位置。这通常通过递归或迭代的方式实现。插入操作的基本步骤如下:
1. 如果树为空,新节点成为根节点。
2. 如果树不为空,从根节点开始,比较新节点的值与当前节点的值。
3. 如果新节点的值较小,向左子树递归;如果较大,向右子树递归。
4. 当找到一个空的子节点时,将新节点插入该位置。
以下是一个简单的插入操作实现的伪代码:
```pseudo
function insert BST, newNode
if BST is empty
BST = newNode
else
curr
```
0
0





