工程问题解决:利用动力学仿真快速定位并解决柔性绳索设计中的实际问题
发布时间: 2024-12-26 04:13:06 阅读量: 9 订阅数: 11 


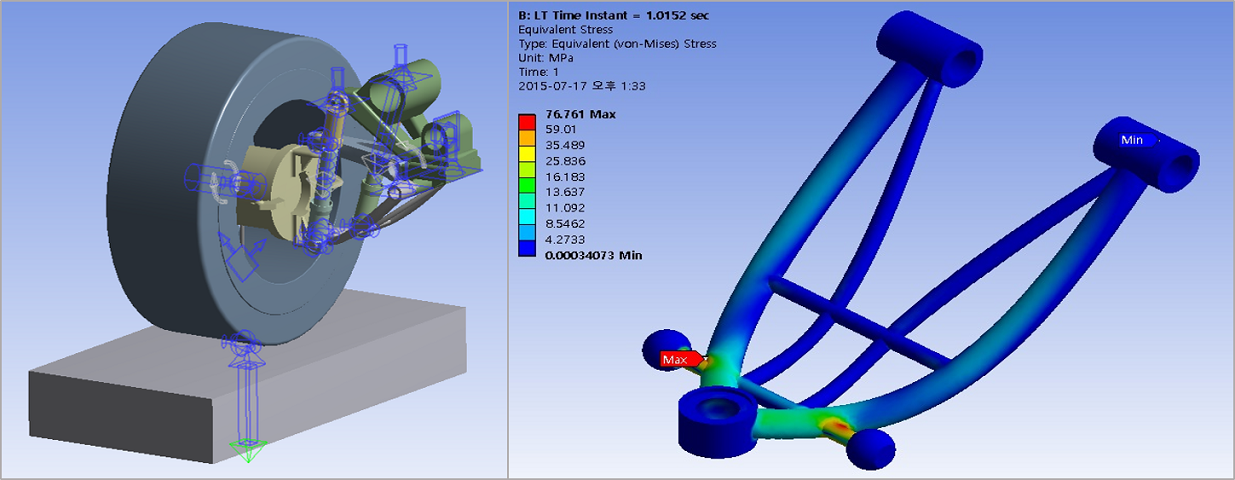
柔性绳索在空气阻力作用下的动力学仿真研究 (2010年)
# 摘要
本论文深入探讨了动力学仿真在柔性绳索设计与分析中的应用,涵盖从基础理论到实际问题解决的全面过程。首先,建立了柔性绳索的动力学模型,详细分析了绳索的物理特性与动力学模型的关系,并介绍了仿真模型的构建流程。随后,探讨了柔性绳索设计中常见问题的仿真模拟,包括振动稳定性分析、动力学响应及与连接件的相互作用。此外,本文还讨论了动力学仿真在问题诊断中的实际应用,提供了仿真数据的分析、故障预测与改进策略,并通过实例研究展示了仿真技术解决实际问题的效果。最后,展望了动力学仿真技术与柔性绳索设计领域的未来发展趋势,包括新兴仿真软件的应用前景及跨学科融合的可能性。
# 关键字
动力学仿真;柔性绳索;模型构建;稳定性分析;故障预测;设计改进
参考资源链接:[ANSYS/LS-DYNA模拟:柔性绳索在空气阻力下的动力学仿真](https://wenku.csdn.net/doc/181skmdqh5?spm=1055.2635.3001.10343)
# 1. 动力学仿真的基础与应用
## 简介
动力学仿真是一种利用计算方法模拟物体或系统在受力作用下的动态行为的技术。它在工程设计、产品开发和问题诊断等领域发挥着越来越重要的作用。
## 动力学仿真的基础
动力学仿真的基础涉及多物理场的交叉学科知识,包括但不限于经典力学、连续介质力学和数值分析。其核心是通过建立准确的数学模型和算法,模拟复杂的动力学过程,并通过仿真实验来预测系统的行为。
## 动力学仿真应用的意义
在实际应用中,动力学仿真可帮助工程师优化设计,减少物理原型的试验次数,降低研发成本。在产品投入市场前,仿真可以提前识别潜在的问题,并验证设计的可行性。
通过本章的介绍,我们将逐步揭示动力学仿真如何在各种场景中扮演关键角色,不仅限于产品设计阶段,还贯穿于整个产品生命周期。下一章,我们将详细探讨柔性绳索动力学模型的建立。
# 2. 柔性绳索动力学模型的建立
## 2.1 绳索物理特性的理论基础
### 2.1.1 材料力学中绳索的性质分析
在材料力学的范畴内,柔性绳索作为一类应用广泛的结构元件,其物理特性主要受到材料组成、截面形状以及制备工艺的影响。考虑到本文的篇幅限制,本节将集中于讨论柔性绳索的弹性模量、泊松比、以及拉伸性能。
- **弹性模量**:弹性模量是材料力学中描述材料抵抗形变能力的重要参数,它通过应力与应变之间的比值来定义。对于绳索材料而言,弹性模量通常表示材料在拉伸过程中抵抗形变的刚度。低弹性模量的材料意味着绳索在受到相同外力作用时,会发生更大的变形。
```mathematica
公式:E = σ / ε
解释:E表示弹性模量,σ表示应力(单位面积上的力),ε表示应变(形变量与原始长度的比值)。
```
- **泊松比**:泊松比是一个无量纲的系数,用来描述材料在轴向拉伸或压缩时,横向与纵向尺寸变化之间的关系。对于柔性绳索,泊松比小的材料在受到拉伸时,横向收缩较小,表现出更好的稳定性。
- **拉伸性能**:拉伸性能是材料在单轴拉伸下应力-应变关系的表征。绳索在实际应用中,特别是在动态负载下,其拉伸性能将直接影响其使用性能和寿命。
### 2.1.2 动力学模型与绳索弯曲特性的关系
柔性绳索在实际应用中常常处于复杂的动力学环境中,例如绳索在高速运动过程中的振动、冲击以及与其它物体的接触碰撞。因此,构建一个准确的动力学模型对于预测和控制绳索行为至关重要。
绳索的弯曲特性可通过经典动力学方程来描述,包括但不限于:
- **弯曲刚度**:影响绳索在受到外力作用时弯曲的能力。在仿真模型中,通过赋予绳索适当的弯曲刚度来模拟其弯曲行为。
- **阻尼比**:衡量绳索在振动过程中能量损耗的参数,与绳索振动衰减的速度有关。
- **惯性项**:考虑绳索质量分布对动力学特性的影响,尤其是当绳索处于动态条件下的加速度运动时,惯性项对动力学响应的影响变得更加显著。
构建一个精确的绳索动力学模型需要充分考虑这些特性,并通过实验数据进行校正和验证,以确保模型的可靠性。这样的模型可以帮助工程师在设计阶段对潜在问题进行预测和解决,从而减少设计周期和成本。
```mathematica
动力学模型示例:考虑绳索动态行为,需要解偏微分方程,如:
\[ \rho A \frac{\partial^2 u}{\partial t^2} + E I \frac{\partial^4 u}{\partial x^4} + c \frac{\partial u}{\partial t} = f(x,t) \]
解释:ρ是材料密度,A是横截面积,u是绳索中某点沿x轴的位移,t是时间,EI是绳索的弯曲刚度,c是阻尼系数,f(x,t)是作用在绳索上的外力分布。
```
## 2.2 动力学仿真模型的构建流程
### 2.2.1 仿真软件选择与模型前处理
在开始构建动力学仿真模型之前,选择一款合适的仿真软件是至关重要的一步。当前市面上有多种仿真工具,如ANSYS、ABAQUS、COMSOL Multiphysics等,它们各有特色,适用于不同类型和规模的问题。
选择软件时,需要考虑的因素包括:
- **适用性**:软件是否支持柔性绳索这类结构的精确建模和求解。
- **易用性**:界面是否直观,学习曲线是否平缓。
- **后处理能力**:结果展示是否丰富,是否易于从仿真数据中提取有用的工程信息。
- **计算效率**:求解大规模问题时的速度和稳定性。
选定仿真软件后,进行模型前处理,这包括定义材料属性、边界条件、初始条件、网格划分等。在模型前处理阶段,需要特别注意以下几点:
- **材料属性的精确定义**:根据实际材料的物理特性,准确设定弹性模量、泊松比、密度等参数。
- **精细的网格划分**:确保模型的计算精度,特别是在考虑动态行为时,合理划分网格对于准确捕捉振动特性至关重要。
- **边界和初始条件的设定**:这些条件直接影响到仿真结果的正确性,需要根据实际问题进行设定。
### 2.2.2 网格划分与材料属性定义
在仿真软件中,网格划分是将连续的模型离散化为有限元的过程。对于柔性绳索这类细长结构,沿绳索长度方向使用一维或二维单元,而在截面方向使用高阶单元以捕捉弯曲效应,是一种常见的做法。
- **一维单元**:线性或非线性单元,适用于描述绳索的拉伸和扭转行为。
- **二维单元**:如果需要考虑绳索的剪切效应或横向变形,可以使用壳单元。
- **高阶单元**:在需要高精度求解的情况下,使用高阶单元可以更准确地近似复杂的应力场和应变场。
材料属性的定义是基于实验数据和理论计算获得的。在柔性绳索的仿真中,除了弹性模量、泊松比之外,还需要定义绳索的质量密度。此外,对于动态分析,还需要定义材料的阻尼特性。阻尼特性可以通过实验获取或根据经验公式估算。在仿真软件中,可以通过设置材料库中预定义的材料类型或输入自定义参数来定义材料属性。
### 2.2.3 边界条件及载荷的应用
在动力学仿真中,边界条件和载荷的正确设定至关重要,因为它们定义了问题的物理环境,直接影响到仿真结果的准确性。本节将详细介绍边界条件设置和载荷应用的理论和实践方法。
在柔性绳索的仿真模型中,常见的边界条件包括:
- **固定端(Fixed End)**:绳索的一端完全固定,不允许任何位移和转动。此条件下绳索的末端位移和旋转度均为零。
- **自由端(Free End)**:与固定端相对,绳索的末端可以自由移动,无任何约束。
- **简支端(Simply Supported)**:绳索的两端在垂直方向受到约束,允许在水平方向移动和绕垂直轴旋转。
- **滑移边界(Sliding Boundary)**:绳索可以在固定表面上滑动,但不承受垂直于表面的力。
载荷的应用也是决定仿真结果准确性的重要因素。柔性绳索上可能受到的载荷类型包括:
- **静力载荷**:例如,绳索在恒定拉力下的受力分析。
- **动态载荷**:例如,在冲击或周期性激励下的受力分析。
- **自重**:对于长距离或跨界的绳索而言,自重引起的重力效应不可忽略。
- **环境载荷**:例如,风力、水流等环境因素对绳索的影响。
在仿真软件中,可以通过定义载荷步(Load Step)来模拟不同类型的载荷作用情况。载荷步允许用户定义载荷随时间的变化,从而模拟复杂的动态过程。例如,在分析绳索在受到冲击载荷时的动力学行为时,可以设置一个短时间内的急剧加载,然后随时间逐渐减小载荷到零。
```mathematica
代码示例:在ANSYS中定义边界条件和载荷的APDL命令序列
/PREP7
! 定义材料属性
MP,EX,1,210000 ! 定义弹性模量
MP,PRXY,1,0.3 ! 定义泊松比
MP,DENS,1,7800 ! 定义质量密度
! 定义绳索截面特性
SECTYPE,1,BEAM
```
0
0






