【栈与递归核心攻略】：深入浅出，掌握编程灵魂

# 1. 栈与递归基础概念

## 1.1 简介
在计算机科学中，栈（Stack）是一种后进先出（LIFO, Last In First Out）的数据结构，它只允许在容器的一端进行插入或删除数据的操作。递归（Recursion）则是一种编程思想，它允许函数调用自身，以解决问题的子集。栈和递归是两种密切相关且在算法设计中应用广泛的理论概念。

## 1.2 栈的作用
栈的操作十分简单，主要包含进栈（push）、出栈（pop）、查看栈顶元素（peek）等操作。在算法中，栈被用于解决诸如括号匹配、表达式求值和深度优先搜索等许多问题，其本质在于它可以帮助我们以一种有序和受控的方式管理数据。

## 1.3 递归的特性
递归的关键在于将问题分解为更小的子问题，并重复此过程直至达到基本情况（base case），然后逐层返回解答。递归在处理具有自相似结构的问题时尤其有效，如树的遍历、汉诺塔问题等。然而递归也可能带来效率问题，特别是当递归深度过深或子问题重叠时，可能导致栈溢出或性能瓶颈。

在接下来的章节中，我们将深入探讨栈与递归的理论和实践，通过具体的实现方法和应用场景来展示它们在解决复杂问题中的强大能力。

# 2. 栈数据结构的理论与实践

## 2.1 栈的基本原理和实现
### 2.1.1 栈的定义与特性

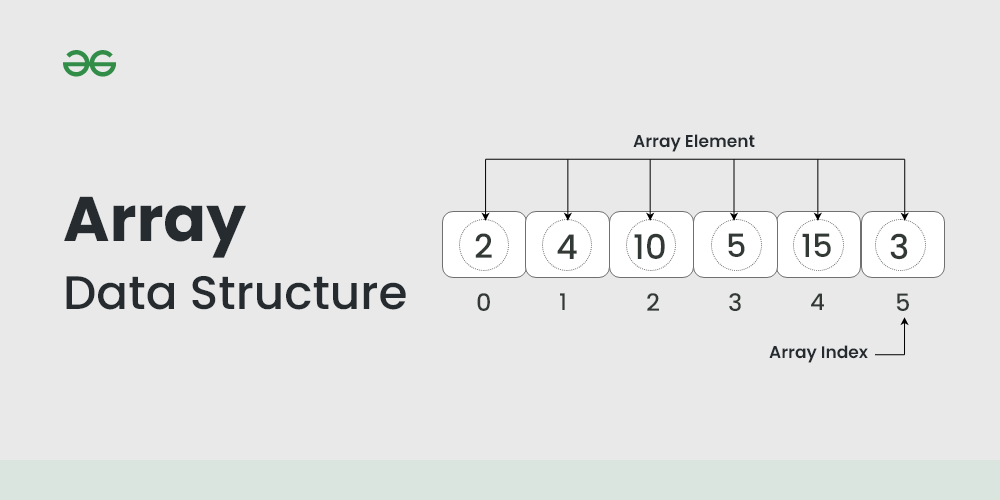
栈是一种后进先出（Last In First Out, LIFO）的数据结构，它有以下几个基本特性：

- 顺序存储：通常栈内部元素按照线性序列的顺序进行存储，可以使用数组或者链表实现。
- 基本操作：栈的主要操作包括入栈（push）和出栈（pop），分别对应元素的添加和移除。此外还有查看栈顶元素（peek）和检查栈是否为空（isEmpty）等操作。
- 独有特性：栈不允许在除了栈顶之外的其他位置进行添加或者移除操作。

栈被广泛应用于各种算法和程序设计之中，例如函数调用的栈帧管理、深度优先搜索（DFS）、浏览器的前进后退功能等。

### 2.1.2 栈的数组实现

数组实现的栈需要考虑几个关键点：

- 索引：通常使用一个整数索引变量来跟踪栈顶元素的位置。
- 存储空间：数组需要有足够的空间来存储栈中的元素。
- 边界条件：当栈为空时，索引应指向数组开始的位置；当栈满时，索引的下一个位置是数组的末尾。

下面是一个简单的栈的数组实现示例代码：

class StackArray:
    def __init__(self):
        self.stack = []
    def push(self, item):
        self.stack.append(item)
    def pop(self):
        if self.isEmpty():
            raise IndexError("pop from an empty stack")
        return self.stack.pop()
    def peek(self):
        if self.isEmpty():
            return None
        return self.stack[-1]
    def isEmpty(self):
        return len(self.stack) == 0
    def size(self):
        return len(self.stack)

### 2.1.3 栈的链表实现

与数组实现相比，链表实现栈不需要连续的内存空间，更适合动态地添加和删除元素。链表实现的栈主要由节点组成，每个节点包含数据和指向下一个节点的指针。

链表栈的基本操作实现如下：

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class StackLinkedList:
    def __init__(self):
        *** = None
    def push(self, data):
        new_node = Node(data)
        new_node.next = ***
        *** = new_node
    def pop(self):
        if self.isEmpty():
            raise IndexError("pop from an empty stack")
        pop_node = ***
        *** = ***.next
        return pop_node.data
    def peek(self):
        if self.isEmpty():
            ***
        ***.data
    def isEmpty(self):
        *** is None

## 2.2 栈的操作详解

### 2.2.1 入栈与出栈操作

在栈的操作中，入栈（push）和出栈（pop）是最核心的操作。

- 入栈操作：新元素被添加到栈顶。
- 出栈操作：栈顶元素被移除并返回。

这两个操作的复杂度都为O(1)，意味着它们执行的速度非常快，不依赖于栈中元素的个数。

### 2.2.2 栈的其他操作及应用场景

除了核心的push和pop操作外，栈还可以进行以下操作：

- 查看栈顶元素（peek）：返回栈顶元素但不移除它。
- 检查栈是否为空（isEmpty）：判断栈内是否有元素。
- 获取栈的大小（size）：返回栈内的元素个数。

应用场景包括：

- 函数调用跟踪：编译器使用栈来保存函数调用时的状态，便于函数返回和局部变量的管理。
- 表达式求值：通过将操作符放入栈中，可以进行后缀表达式等的计算。
- 深度优先搜索（DFS）：在搜索过程中使用栈来维护路径信息。

## 2.3 栈在算法中的应用

### 2.3.1 递归算法与栈

递归算法通常与栈紧密相关，因为每进入一层递归调用，函数的状态就会被压入栈中。当递归返回时，就会从栈中弹出之前的状态。

递归的栈空间消耗主要由以下几个因素决定：

- 递归深度：递归的层数。
- 每层的状态大小：每个递归层中需要保存的局部变量和参数大小。
- 调用栈空间的开销：包括栈帧的创建、函数参数的传递等。

### 2.3.2 表达式求值与栈

表达式求值是栈的一个典型应用场景。其中，后缀表达式求值是最直接的应用之一。在后缀表达式中，运算符位于操作数之后，计算时使用一个栈来暂存操作数。

求值步骤大致如下：

1. 从左到右扫描表达式。
2. 遇到操作数时，将其压入栈中。
3. 遇到运算符时，从栈中弹出所需数量的操作数，执行运算，并将结果压回栈中。
4. 表达式遍历完成后，栈顶元素即为表达式的结果。

### 2.3.3 深度优先搜索(DFS)与栈

深度优先搜索是一种用于遍历或搜索树或图的算法。在DFS中，使用栈来记录访问路径：

- 访问一个节点时，将其标记为已访问，并将该节点压入栈中。
- 当回溯时，从栈中弹出一个节点进行下一轮访问。

使用栈的DFS确保了路径的回溯，使得算法能够遍历到图中的所有节点（如果图是连通的话）。

# 3. 递归的理论与实践

## 3.1 递归函数的工作原理

### 3.1.1 递归的定义与条件

递归函数是一种在定义中调用自身的函数，这种定义方式在计算机科学中是非常强大的，它允许问题以分而治之的方式被简化成更小的子问题。递归的核心在于定义一个或多个递归条件（base cases），当这些条件满足时，递归将停止，返回一个结果。同时，还需要定义一个或多个递归步骤（recursive step），在这些步骤中，函数将自身调用以解决更小的子问题。

递归函数必须遵循的条件包括：

- 至少有一个基线条件（base case），用于终止递归。
- 每次递归调用都应使问题规模逐渐减小，以保证递归最终能够达到基线条件。
- 不应该无限制地递归，避免造成栈溢出错误。

代码示例可以帮助理解递归定义：

def factorial(n):
    if n == 0:  # 基线条件
        return 1
    else:
        return n * factorial(n-1)  # 递归步骤

### 3.1.2 递归的基本结构

递归函数的基本结构通常包括两个主要部分：

- **基线条件（Base Case）**: 定义了最简单的问题实例，可以直接给出答案，无需进一步递归。
- **递归步骤（Recursive Step）**: 这部分将问题规模缩小，通过调用递归函数自身来处理缩小规模后的子问题。

一个递归函数要能正确地工作，它的递归步骤应该不断接近基线条件，且每次递归调用都是向前进展，直到基线条件成立为止。

理解递归的结构需要把握递归的分解与归纳的原理，分解是将大问题化为小问题，归纳则是由小问题的解组合成大问题的解。

## 3.2 递归与迭代的比较

### 3.2.1 递归与迭代的优势与局限

在算法实现中，递归和迭代是最常用的两种方法，它们各自具有优势和局限性。

递归的优势在于：
- 代码简洁易懂：递归通常比对应的迭代代码更加简洁，对于树形或分形结构的算法特别有用。
- 结构清晰：递归的结构天然适合表示有明显递归定义的数学函数。

递归的局限包括：
- 性能开销：递归函数的每一次调用都需要额外的内存来保存状态信息，而递归层次过深可能导致栈溢出。
- 效率问题：重复计算相同子问题可能导致效率低下。

迭代的优势在于：
- 效率高：迭代避免了递归中的重复计算和栈空间消耗。
- 易于理解：在某些情况下，迭代的逻辑更符合人们的直觉。

迭代的局限主要表现在：
- 编码复杂度：对于复杂的递归算法，迭代版本可能需要更复杂的循环控制逻辑。
- 状态管理：在迭代中，需要手动管理状态，代码可能因此变得复杂。

### 3.2.2 实际问题中迭代与递归的选择

选择迭代还是递归取决于具体的场景：

- 对于简单的线性问题，迭代通常是更好的选择。
- 当问题自然可以分解为子问题时，递归的使用会更加直观。
- 在某些情况下，递归可以提供更清晰和简洁的解决方案，尤其是在处理树或图的问题时。

在实际编程中，应根据问题的复杂性、性能要求、以及开发时间来选择最合适的实现方法。

## 3.3 递归的性能分析与优化

### 3.3.1 递归的性能问题

递归的性能问题主要集中在两个方面：

- **内存开销**：递归函数调用自身的每一次递归都会产生一个新的函数调用堆栈，这会增加内存的使用。
- **重复计算**：递归可能导致对同一个子问题的多次计算，尤其在没有合理缓存的情况下。

### 3.3.2 尾递归优化技术

尾递归是一种特殊的递归形式，它出现在函数的最后一个操作中，而函数的返回值仅作为参数传递给另一个函数调用。在支持尾调用优化的语言中，尾递归可以被编译器优化，避免栈空间的消耗，提高性能。

例如：

def tail_recursive_factorial(n, accumulator=1):
    if n == 0:
        return accumulator
    else:
        return tail_recursive_factorial(n-1, accumulator * n)

### 3.3.3 记忆化递归（动态规划）

记忆化递归，也称为递归与缓存相结合的策略，是一种用于优化递归算法的技术。通过保存已经计算过的子问题的结果，避免重复计算，这通常可以显著提高性能。

以计算斐波那契数列为例：

def memoized_fibonacci(n, memo=None):
    if memo is None:
        memo = {0: 0, 1: 1}
    if n not in memo:
        memo[n] = memoized_fibonacci(n-1, memo) + memoized_fibonacci(n-2, memo)
    return memo[n]

这种方式在某些情况下也被称为动态规划，它经常被用来解决具有重叠子问题的算法问题。

# 4. 栈与递归在实际编程中的应用

## 4.1 栈的应用实例

### 4.1.1 编译器中的栈应用

编译器是程序设计中不可或缺的一部分，它负责将高级语言编写的源代码转换为机器语言。栈在编译器中扮演了核心角色，尤其是在语法分析阶段。编译器使用栈来存储中间构造，如操作符的优先级和括号。

在编译过程中，编译器需要理解并转换表达式。使用栈结构，编译器能够处理不同优先级的操作符，例如，栈允许编译器在遇到一个优先级高的操作符时，暂时存储低优先级的操作符。再比如，栈用于跟踪括号匹配，确保程序的结构正确。

编译器中的编译过程通常分为四个主要阶段：词法分析、语法分析、语义分析和代码生成。在语法分析阶段，一个称为"逆波兰表示法"（后缀表达式）的技术常被用来转换复杂的中缀表达式。这一步骤中，编译器将中缀表达式中的操作符和操作数重新排列，使用栈来记录和管理操作符的顺序。

#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>

#define MAX 100

int top = -1;
char stack[MAX];

void push(char item) {
    if (top == MAX - 1) {
        printf("\nStack Overflow.");
    } else {
        stack[++top] = item;
    }
}

char pop() {
    if (top == -1) {
        printf("Stack Underflow.");
        exit(1);
    } else {
        return stack[top--];
    }
}

int isOperator(char x) {
    if (x == '+' || x == '-' || x == '*' || x == '/' || x == '^') {
        return 1;
    } else {
        return 0;
    }
}

int precedence(char op) {
    if (op == '+' || op == '-') {
        return 1;
    } else if (op == '*' || op == '/') {
        return 2;
    } else if (op == '^') {
        return 3;
    }
    return 0;
}

void InfixToPostfix(char* infixexpr) {
    char c;
    push('(');
    strcat(infixexpr, ")");
    int i;
    for (i = 0; infixexpr[i] != '\0'; i++) {
        c = infixexpr[i];
        if (c == '(') {
            push(c);
        } else if (isdigit(c)) {
            printf("%c ", c);
        } else if (isOperator(c)) {
            while (isOperator(stack[top]) && precedence(c) <= precedence(stack[top])) {
                printf("%c ", pop());
            }
            push(c);
        } else if (c == ')') {
            while (stack[top] != '(') {
                printf("%c ", pop());
            }
            pop();
        }
    }
    while (stack[top] != -1) {
        printf("%c ", pop());
    }
}

int main() {
    char infixexpr[] = "A*(B+C)/D";
    printf("Infix Expression: %s\n", infixexpr);
    printf("Postfix Expression: ");
    InfixToPostfix(infixexpr);
    return 0;
}

这段代码将中缀表达式转换为后缀表达式。每个字符都被依次读入，操作符根据它们的优先级被压入栈中或弹出并打印。此过程极大地依赖于栈数据结构，展示了栈如何简化编译器中的复杂操作。

### 4.1.2 括号匹配与栈

在编程语言中，括号是常见的符号，用于分组或指定操作的顺序。括号匹配检查是编译器语法分析的一部分。在这个场景中，栈用于验证括号是否正确匹配。

括号匹配算法的基本思路是遍历表达式的每个字符。每遇到一个开放括号，如左括号`(`，就将其压入栈中；每遇到一个闭合括号，如右括号`)`，就从栈中弹出一个括号进行匹配。若最终栈为空且所有字符都已遍历，则说明表达式中的括号是匹配的。

下面是一个简单的括号匹配的代码示例：

def is_parentheses_balanced(expression):
    stack = []
    opening_parentheses = '([{'
    closing_parentheses = ')]}'
    parentheses_map = dict(zip(closing_parentheses, opening_parentheses))
    for char in expression:
        if char in opening_parentheses:
            stack.append(char)
        elif char in closing_parentheses:
            if not stack or parentheses_map[char] != stack.pop():
                return False
    return not stack

# 测试代码
expression = "{[()()]}"
print(is_parentheses_balanced(expression))  # 输出应为 True

在这个函数中，当遇到一个闭合括号时，我们检查栈顶元素是否与之匹配。若匹配，则将栈顶元素弹出；若不匹配，则直接返回`False`。若表达式全部处理完毕后栈为空，则说明括号匹配。

### 4.1.3 后缀表达式与栈

后缀表达式，也称为逆波兰表示法，是一种不需要括号来标识操作符优先级的算术表达式。在后缀表达式中，操作符位于它所操作的两个运算对象的后面。例如，中缀表达式`(A + B) * C`可以表示为后缀表达式`A B + C *`。

栈在这类表达式的评估中起着至关重要的作用。下面是一个后缀表达式的评估算法：

1. 创建一个空栈。
2. 从左到右扫描后缀表达式。
3. 如果扫描到的是操作数，就将它压入栈。
4. 如果扫描到的是操作符，则从栈中弹出两个操作数，执行操作，再将结果压回栈。
5. 表达式扫描完毕后，栈顶元素即为表达式的结果。

下面是用Python实现的一个后缀表达式的评估：

def evaluate_postfix(expression):
    stack = []
    operators = set(['+', '-', '*', '/', '^'])
    for char in expression.split():
        if char not in operators:
            stack.append(int(char))
        else:
            operand2 = stack.pop()
            operand1 = stack.pop()
            if char == '+':
                stack.append(operand1 + operand2)
            elif char == '-':
                stack.append(operand1 - operand2)
            elif char == '*':
                stack.append(operand1 * operand2)
            elif char == '/':
                stack.append(operand1 / operand2)
            elif char == '^':
                stack.append(operand1 ** operand2)
    return stack.pop()

# 测试代码
expression = "2 3 + 9 * 3 / 10 +"
print(evaluate_postfix(expression))  # 输出应为 12

在这个例子中，表达式`2 3 + 9 * 3 / 10 +`被正确地求值，演示了栈如何用于后缀表达式的计算。

## 4.2 递归的应用实例

### 4.2.1 目录遍历与递归

在文件系统操作中，递归是一种常用的技术，用于遍历目录树结构。递归遍历目录涉及访问一个目录中的所有文件和子目录，当遇到一个子目录时，相同的遍历函数会被递归调用。

递归的目录遍历函数通常遵循这样的结构：

1. 访问当前目录。
2. 遍历目录中的所有文件，对每个文件执行所需的处理。
3. 遍历目录中的所有子目录。
4. 对每个子目录递归调用目录遍历函数。

以下是用Python编写的递归遍历目录的简单示例：

import os

def list_files_recursively(path):
    for entry in os.listdir(path):
        full_path = os.path.join(path, entry)
        if os.path.isdir(full_path):
            print("Directory:", full_path)
            list_files_recursively(full_path)  # 递归调用
        else:
            print("File:", full_path)

# 测试代码
list_files_recursively('/path/to/directory')  # 用实际路径替换

在这个例子中，`list_files_recursively`函数会打印出指定目录下的所有文件和子目录的路径。递归调用自身来处理每个子目录。

### 4.2.2 分治算法与递归

分治算法是一种递归策略，它将问题分解为更小的子问题，独立地解决这些子问题，然后再将它们合并成最终结果。最著名的分治算法之一是快速排序算法，它使用分治策略将一个数组分成两个子数组，一个包含小于基准值的元素，另一个包含大于基准值的元素，然后递归地排序这两个子数组。

快速排序的基本步骤是：

1. 选择基准值（pivot）。
2. 分割数组，所有小于基准值的元素放在基准值的左边，所有大于基准值的元素放在基准值的右边。
3. 递归地对基准值左右两边的子数组进行步骤1和步骤2。

下面是一个快速排序的Python实现：

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort(left) + middle + quicksort(right)

# 测试代码
unsorted_array = [3, 6, 8, 10, 1, 2, 1]
sorted_array = quicksort(unsorted_array)
print(sorted_array)

在这个例子中，数组通过递归的快速排序算法被排序。

### 4.2.3 图论中的递归算法

图论是研究图的数学理论和应用。图由节点（顶点）和连接这些节点的边组成。递归算法在图论中有多种应用，比如深度优先搜索（DFS）。DFS通过递归或栈遍历图的所有可达节点，并且可以用来检测图中是否存在回路。

DFS算法的基本步骤为：

1. 标记起始节点为已访问。
2. 访问起始节点，并将它加入到路径中。
3. 递归地对所有未访问的邻接节点执行步骤1和步骤2。

下面是DFS算法的一个递归实现示例：

def DFS(graph, node, visited):
    if node not in visited:
        print(node, end=' ')
        visited.add(node)
        for neighbour in graph[node]:
            DFS(graph, neighbour, visited)

# 测试代码
graph = {'A': ['B', 'C'], 'B': ['D', 'E'], 'C': ['F'], 'D': [], 'E': ['F'], 'F': []}
visited = set()
DFS(graph, 'A', visited)  # 输出应为 A B D E C F

在这个例子中，`graph`是一个简单的表示图的数据结构，`DFS`函数递归地遍历这个图。

## 4.3 栈与递归在高级数据结构中的作用

### 4.3.1 栈与树结构的结合应用

在计算机科学中，树是一种重要的数据结构，用于表示层次关系。栈可以与树结合使用，特别是在实现树的遍历（如深度优先搜索）时。

树的深度优先搜索（DFS）递归地探索尽可能深的节点，直到没有其他节点可以访问为止，然后回溯。在这个过程中，栈用于存储下一个要访问的节点。每次递归调用都将新的节点压入栈中，并在完成当前节点的子节点探索后弹出栈顶的节点。

以下是树的DFS递归算法示例，使用Python实现：

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def DFS(node):
    if node is not None:
        print(node.val)
        DFS(node.left)
        DFS(node.right)

# 测试代码
# 创建一个简单的二叉树
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

DFS(root)  # 输出应为 1 2 4 5 3

在这个例子中，递归函数`DFS`遍历树的所有节点，显示节点的值。

### 4.3.2 递归在二叉树遍历中的运用

二叉树是一种特殊类型的树，其中每个节点最多有两个子节点，通常称它们为左子节点和右子节点。在二叉树的遍历中，递归是实现三种主要遍历方法（前序、中序和后序）的常用方法。

前序遍历访问当前节点，然后递归地遍历左子树，最后递归地遍历右子树。
中序遍历递归地遍历左子树，访问当前节点，然后递归地遍历右子树。
后序遍历递归地遍历左子树，递归地遍历右子树，最后访问当前节点。

递归的二叉树遍历可以用以下伪代码表示：

function Preorder(node)
    if node is not null
        print node.value
        Preorder(node.left)
        Preorder(node.right)

function Inorder(node)
    if node is not null
        Inorder(node.left)
        print node.value
        Inorder(node.right)

function Postorder(node)
    if node is not null
        Postorder(node.left)
        Postorder(node.right)
        print node.value

### 4.3.3 栈在回溯问题中的应用

回溯是一种算法思想，用于解决需要探索多种可能性的问题。回溯算法通常采用递归实现，并且在遇到不可能或不希望的情况时，使用栈结构来回溯到之前的某个状态。

回溯算法的关键点是：

1. 尝试所有可能的候选解。
2. 如果找到一个解，则停止搜索。
3. 如果当前候选解不能导致一个有效解，则回溯并尝试另一个候选解。

例如，在解决八皇后问题（在8x8的棋盘上放置8个皇后，使得没有两个皇后可以互相攻击）时，可以使用回溯算法。栈可以帮助记录每一步的状态，以便在需要时回溯。

下面是一个回溯算法解决八皇后问题的伪代码示例：

function SolveNQueens(board, row)
    if row == size of board
        print solution
        return
    for col from 0 to size of board - 1
        if board is safe to place queen at (row, col)
            place queen at (row, col)
            SolveNQueens(board, row + 1)
            remove queen from (row, col) // backtracking step

在上述伪代码中，算法尝试在每一行放置一个皇后，并在下一行递归。如果无法放置，则回溯到上一行并尝试不同的列。

以上内容展示了栈与递归在实际编程中的广泛应用，从编译器的构造到高级数据结构的处理。这些是数据结构和算法中基本但关键的概念，对任何希望深入理解计算机科学的读者来说，都是不可或缺的财富。

# 5. 递归问题的调试与测试

递归问题的调试与测试是确保递归算法正确性和性能的关键环节。递归算法的复杂性往往使得问题难以一眼看出，因此，需要一些特别的调试技巧和测试方法来处理这些问题。

## 5.1 递归问题的调试技巧

### 5.1.1 递归逻辑错误的识别与修正

递归逻辑错误可能包括无限递归、参数传递错误、边界条件处理不当等。识别这些错误需要对递归逻辑有深刻理解。

一个有效的调试方法是逐步跟踪递归过程。这可以通过打印输出当前递归层次和相关参数来实现。例如，下面是一个简单的递归函数，它计算阶乘，并通过打印语句来跟踪递归过程：

def factorial(n):
    if n == 0:
        return 1
    else:
        print(f"Computing factorial({n}) with n={n}")
        return n * factorial(n - 1)

factorial(5)

在实际调试中，使用专业的调试工具可以更加方便。大多数现代IDE（如PyCharm, Visual Studio Code等）都支持设置断点和单步执行代码的功能。通过这些工具，我们可以观察变量的变化，逐步执行每一行代码，确保递归调用按预期执行。

### 5.1.2 调试工具在递归中的应用

现代调试工具提供了丰富的功能，可以帮助开发者更有效地调试递归代码。这些工具通常包括：

- **断点：** 在递归函数的关键点设置断点，如递归调用前后。
- **变量监视：** 监视递归过程中变量的变化情况。
- **调用栈视图：** 查看当前的函数调用栈，快速定位递归的深度和位置。
- **条件断点：** 当满足特定条件时才中断执行，这对于处理深层次递归问题非常有用。

下面是一个使用Visual Studio Code进行调试的示例。首先设置断点在递归函数调用的地方，然后逐步执行，观察调用栈的变化。

Debugger面板显示：
- 当前调用栈
- 局部变量和表达式的值
- 下一步执行的行

![Debugger view in Visual Studio Code](***

在这个视图中，开发者可以实时查看递归调用的参数值变化，以及通过调用栈查看递归的深度和历史调用。

## 5.2 递归算法的测试方法

### 5.2.* 单元测试与递归函数

单元测试是验证函数行为与预期相符的实践，尤其对于递归函数来说，编写良好的单元测试是保证正确性的重要手段。编写单元测试时，需要考虑以下几点：

- **测试边界条件：** 对于递归函数，边界条件的测试尤其重要。例如，递归的基准情况是否能正确处理。
- **测试递归的中止条件：** 确保递归能正确中止，不会发生无限递归。
- **测试递归的正确性：** 使用已知结果或特殊情况来验证递归函数的返回值。

下面是一个使用Python的unittest框架进行递归函数测试的示例：

import unittest

class TestRecursion(unittest.TestCase):

    def test_factorial(self):
        self.assertEqual(factorial(0), 1)  # 边界条件测试
        self.assertEqual(factorial(5), 120)  # 一般情况测试

if __name__ == '__main__':
    unittest.main()

### 5.2.2 边界情况分析

边界情况分析是测试递归函数的一个重要方面。开发者需要识别和测试那些可能导致递归行为异常的特殊情况。例如：

- 参数值的极端情况，如非常大或非常小的数值。
- 特殊的输入类型，例如非数字或负数等。

在测试时，应该为这些边界情况设计测试用例，并验证递归函数是否能正确处理。

### 5.2.3 测试递归算法的性能

递归算法的性能测试也是不可缺少的一环。由于递归可能会带来大量的函数调用，因此可能会成为性能瓶颈。

性能测试应关注：

- **时间复杂度：** 递归算法的执行时间是否随输入规模的增长而呈现可接受的增长。
- **空间复杂度：** 递归算法所使用的栈空间是否过量，尤其是在深度递归的情况下。

在性能测试时，可以使用性能分析工具，如Python中的cProfile，来分析函数调用的时间和空间使用情况。这可以帮助开发者发现性能瓶颈，并对算法进行优化。

递归问题的调试与测试是一个既需要技巧又需要经验的过程。通过上述方法，我们可以更加高效地识别和修正递归逻辑错误，以及确保递归算法的正确性和性能。

# 6. 递归思想的扩展与深化

递归思想是计算机科学中的一种基础思想，不仅在算法设计中占据重要地位，而且在理解和处理复杂问题时也显得尤为关键。在本章中，我们将探讨递归思想在解决复杂问题中的应用，并对非传统递归问题进行探索，最后对递归在未来计算机科学中的地位和发展进行展望。

## 6.1 递归思维在复杂问题中的应用

递归思想的核心在于将问题分解为更小的子问题，直到达到一个可以直接解决的基线条件。这一思想尤其适用于复杂问题，因为它可以帮助开发者以自顶向下的方式，逐步深入问题的细节，找到解决方案。

### 6.1.1 递归思维与问题分解

递归思维的关键在于识别问题的相似性，即将当前问题转化为一个或多个更小的子问题。这种方法在解决如树遍历、图搜索和排序等问题时尤其有用。通过递归，我们可以将复杂度高、难以直接处理的问题简化为多个简单问题。

以树的遍历为例，无论是前序遍历、中序遍历还是后序遍历，都可以通过递归函数来实现。每个节点的处理逻辑相同，只是在处理子节点时调用递归函数，这样就将复杂问题转化为了更简单的重复处理。

### 6.1.2 递归在解决复杂系统问题中的应用案例

考虑一个复杂系统的软件开发问题，如编译器的构建。编译器需要从源代码生成机器代码，这个过程涉及到词法分析、语法分析、语义分析、中间代码生成、优化和目标代码生成等多个步骤。递归在语法分析阶段特别有用，如构建解析树（parse tree）时。

另一个例子是网络数据包的路由。每个路由器可以将数据包向目标发送，这个过程可以递归地对每一个路由器进行。每个路由器的决策都基于对目的地和当前网络状态的分析，这个分析过程本身也可以递归进行。

## 6.2 非传统递归问题的探索

递归并非只有一种形式，而是一个包含多种实现与变种的概念。理解这些非传统递归问题的探索可以拓展我们对递归概念的理解。

### 6.2.1 尾递归以外的递归变种

尾递归是递归中的一种特殊情况，其中递归调用是函数体中的最后一个操作。除了尾递归，还有其他一些递归模式，例如分而治之（Divide and Conquer）策略中的递归。在这种策略中，问题被分割为两个或更多的子问题，每个子问题在递归中独立解决，最后将结果合并。

还有部分递归（Partial Recursion），在这种递归中，函数的一部分调用自身。例如，在快速排序算法中，快速排序将数组分成两部分，对其中一部分进行快速排序，这个过程就是部分递归。

### 6.2.2 递归与并发编程

递归与并发编程的结合是一个新兴的领域。在并发环境中，每个递归调用可以在不同的线程或进程中进行，从而提高程序的并行性。这种模式对于解决可以并行处理的大型计算问题尤其有用。

然而，递归与并发的结合也带来了新的挑战，如线程安全、资源共享和同步等问题。解决这些问题需要对并发编程有深入的理解，并且在设计递归算法时考虑如何减少线程间的依赖和冲突。

## 6.3 对递归未来发展的思考

递归作为一个历史悠久的概念，在计算机科学的未来发展中将继续发挥作用。下面对递归理论的未来趋势和在新编程范式中的角色进行探讨。

### 6.3.1 递归理论的未来趋势

随着计算模型的不断演进，递归理论也将继续发展。在函数式编程中，递归是一种核心编程范式，未来可能会看到更多函数式编程的特性被集成到主流编程语言中。此外，编译器优化技术的进步将使递归算法更加高效，特别是在支持尾调用优化的环境中。

### 6.3.2 递归在新编程范式中的角色

递归在新编程范式中的角色可能会变得更加突出。例如，在量子计算中，递归算法可能用于设计量子电路。在机器学习领域，递归神经网络（RNNs）已经在处理序列数据方面显示出巨大的潜力。

递归思想的扩展和深化不仅意味着技术的进步，也预示着计算机科学对复杂性管理的新方法。通过不断地扩展递归的应用场景和优化其性能，递归将继续作为计算机科学中不可或缺的组成部分，推动着这一学科的持续发展。