【复杂网络中的最短路径算法】：大数据分析与网络科学，揭示网络奥秘

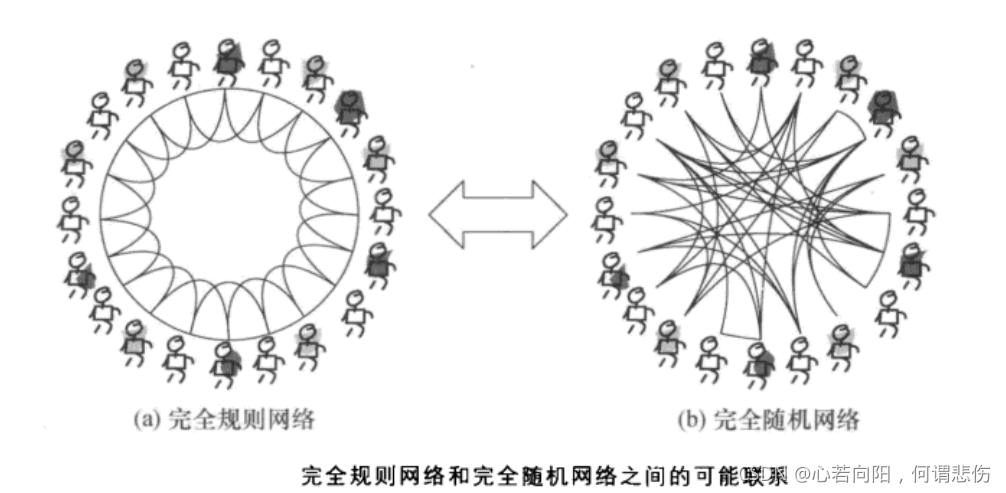
# 1. 复杂网络概述**

复杂网络是一种具有非平凡拓扑结构的网络，其特征包括：

- **小世界效应：**网络中的节点平均距离很小，但同时网络的直径很大。
- **无标度性：**网络中节点的度数分布遵循幂律分布，即少数节点拥有大量连接，而大多数节点的连接较少。
- **社区结构：**网络中的节点可以被划分为不同的社区，社区内部的连接密度较高，而社区之间的连接密度较低。

复杂网络在现实世界中广泛存在，例如社交网络、交通网络、生物网络等。研究复杂网络有助于我们理解这些网络的结构和功能，并为解决实际问题提供新的思路。

# 2. 最短路径算法理论

### 2.1 图论基础

图论是研究图结构及其性质的数学分支。图由两个基本元素组成：顶点和边。顶点表示图中的对象，而边表示顶点之间的连接。

**图的表示：**

* **邻接矩阵：**一个二维数组，其中元素表示顶点之间的权重（如果存在）。
* **邻接表：**一个数组，其中每个元素是一个链表，存储与该顶点相邻的顶点。

**图的性质：**

* **连通性：**如果图中任意两个顶点都可以通过一条路径连接，则该图是连通的。
* **环：**如果图中存在一条从某个顶点出发并返回同一顶点的路径，则该图包含环。
* **权重：**边可以具有权重，表示边上的距离、时间或其他度量。

### 2.2 最短路径问题定义

最短路径问题是找到图中两个指定顶点之间权重最小的路径。

**问题定义：**

给定一个图 G = (V, E)，其中 V 是顶点集，E 是边集，以及两个顶点 s 和 t，求从 s 到 t 的权重最小的路径。

### 2.3 经典最短路径算法

有几种经典的最短路径算法，每种算法都有其优点和缺点。

#### 2.3.1 Dijkstra算法

**算法描述：**

Dijkstra算法使用贪心策略，从源顶点开始，逐步扩展最短路径树，直到到达目标顶点。

**算法步骤：**

1. 初始化所有顶点的距离为无穷大，源顶点的距离为 0。
2. 创建一个优先队列，按距离对顶点进行排序。
3. 从优先队列中弹出距离最小的顶点 v。
4. 对于 v 的所有相邻顶点 w，如果通过 v 到 w 的距离小于当前 w 的距离，则更新 w 的距离。
5. 重复步骤 3 和 4，直到到达目标顶点。

**代码块：**

import heapq

def dijkstra(graph, source):
    """
    Dijkstra算法求最短路径

    参数：
        graph: 图的邻接表表示
        source: 源顶点
    """

    # 初始化距离和优先队列
    distance = {v: float('inf') for v in graph}
    distance[source] = 0
    pq = [(0, source)]

    # 贪心扩展最短路径树
    while pq:
        current_distance, current_vertex = heapq.heappop(pq)

        # 达到目标顶点，结束算法
        if current_vertex == target:
            break

        # 遍历相邻顶点
        for neighbor in graph[current_vertex]:
            distance_to_neighbor = current_distance + graph[current_vertex][neighbor]
            if distance_to_neighbor < distance[neighbor]:
                distance[neighbor] = distance_to_neighbor
                heapq.heappush(pq, (distance_to_neighbor, neighbor))

    return distance

**逻辑分析：**

* 算法使用优先队列来存储顶点及其到源顶点的距离。
* 每次从优先队列中弹出距离最小的顶点，并更新其相邻顶点的距离。
* 算法通过贪心策略逐步扩展最短路径树，直到到达目标顶点。

**参数说明：**

* `graph`：图的邻接表表示。
* `source`：源顶点。

#### 2.3.2 Bellman-Ford算法

**算法描述：**

Bellman-Ford算法使用松弛操作，逐步更新图中所有边的权重，直到所有最短路径的权重都得到正确计算。

**算法步骤：**

1. 初始化所有顶点的距离为无穷大，源顶点的距离为 0。
2. 对于所有边 (u, v, w)，执行松弛操作：如果通过 u 到 v 的距离小于当前 v 的距离，则更新 v 的距离。
3. 重复步骤 2 n-1 次，其中 n 是图中顶点的数量。
4. 检查图中是否存在负权重环。如果存在，则算法无法找到最短路径。

**代码块：**

def bellman_ford(graph, source):
    """
    Bellman-Ford算法求最短路径

    参数：
        graph: 图的邻接表表示
        source: 源顶点
    """

    # 初始化距离
    distance = {v: float('inf') for v in graph}
    distance[source] = 0

    # 松弛操作
    for _ in range(len(graph) - 1):
        for u in graph:
            for v, w in graph[u]:
                if distance[u] + w < distance[v]:
                    distance[v] = distance[u] + w

    # 检查负权重环
    for u in graph:
        for v, w in graph[u]:
            if distance[u] + w < distance[v]:
                return False  # 存在负权重环

    return distance

**逻辑分析：**

* 算法通过多次松弛操作逐步更新边权重。
* 算法执行 n-1 次松弛操作，其中 n 是图中顶点的数量。
* 算法最后检查图中是否存在负权重环。

**参数说明：**

* `graph`：图的邻接表表示。
* `source`：源顶点。

#### 2.3.3 Floyd-Warshall算法

**算法描述：**

Floyd-Warshall算法使用动态规划方法，计算图中所有顶点对之间的最短路径。

**算法步骤：**

1. 初始化一个二维数组 D，其中 D[i, j] 表示从顶点 i 到顶点 j 的最短路径权重。
2. 对于所有顶点 i，设置 D[i, i] 为 0。
3. 对于所有边 (u, v, w)，设置 D[u, v] 为 w。
4. 对于所有顶点 k，遍历所有顶点 i 和 j，如果 D[i, k] + D[k, j] < D[i, j]，则更新 D[i, j]。
5. 算法完成后，D[i, j] 表示从顶点 i 到顶点 j 的最短路径权重。

**代码块：**

def floyd_warshall(graph):
    """
    Floyd-Warshall算法求所有顶点对之间的最短路径

    参数：