最短路径算法的最新进展：前沿技术与应用，探索算法未来

# 1. 最短路径算法概述

最短路径算法是一种计算机科学算法，用于在图或网络中找到两个节点之间具有最小权重的路径。最短路径算法在许多现实世界应用中至关重要，包括交通导航、物流配送和网络优化。

最短路径算法基于图论的基本概念，图论是研究图结构及其性质的数学分支。图由节点（顶点）和连接它们的边组成，每个边都有一个权重，表示沿该边的移动成本。最短路径算法的目标是找到从一个节点到另一个节点的路径，其权重之和最小。

最短路径算法有许多不同的类型，每种类型都适用于特定类型的图和应用。最常用的算法包括 Dijkstra 算法、Floyd-Warshall 算法和 A* 算法。这些算法将在后续章节中详细讨论。

# 2. 最短路径算法理论基础

### 2.1 图论基础

#### 2.1.1 图的定义和表示

**图的定义：**

图是一个数据结构，由一组顶点和一组边组成，其中边连接顶点。顶点通常表示对象，而边表示对象之间的关系。

**图的表示：**

图可以用邻接矩阵或邻接表来表示。

* **邻接矩阵：**一个二维数组，其中元素表示顶点之间的权重。
* **邻接表：**一个数组，其中每个元素是一个链表，存储与该顶点相连的所有边。

#### 2.1.2 图的遍历和搜索算法

**图的遍历：**

* **深度优先搜索 (DFS)：**从一个顶点开始，沿着一条路径遍历图，直到遇到死胡同，然后回溯并尝试另一条路径。
* **广度优先搜索 (BFS)：**从一个顶点开始，遍历图中与该顶点相邻的所有顶点，然后遍历与这些顶点相邻的所有顶点，依此类推。

**图的搜索算法：**

* **Dijkstra算法：**用于查找从一个源顶点到所有其他顶点的最短路径。
* **Floyd-Warshall算法：**用于查找图中所有顶点之间两两之间的最短路径。
* **A*算法：**用于查找从一个源顶点到一个目标顶点的最短路径，同时考虑启发式函数。

### 2.2 最短路径算法原理

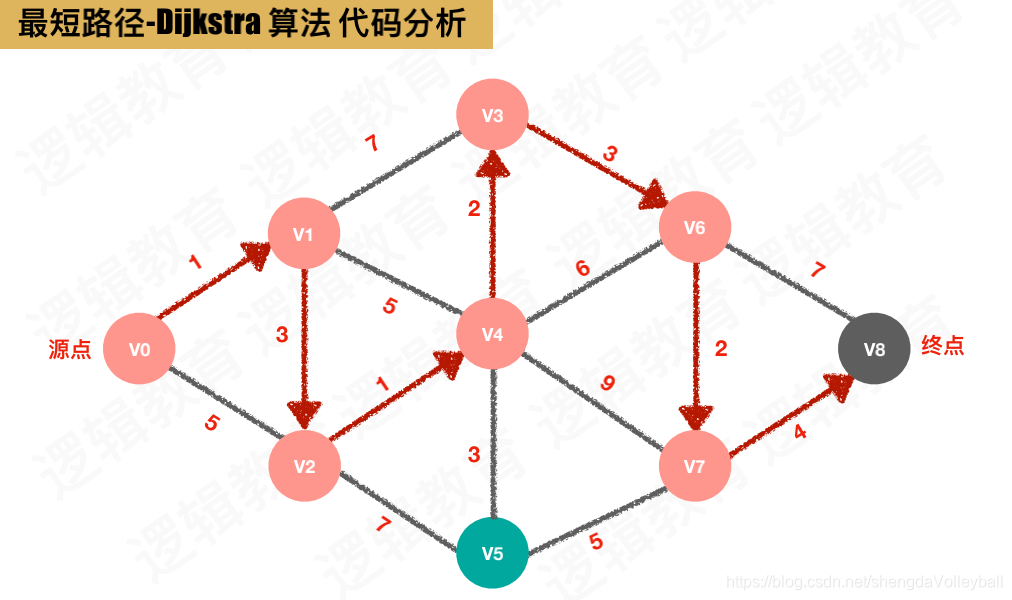
#### 2.2.1 Dijkstra算法

**原理：**

Dijkstra算法从一个源顶点开始，逐步扩展一个最短路径树，直到到达目标顶点。

**算法步骤：**

1. 初始化一个包含所有顶点的集合 `S`，并将其标记为未访问。
2. 从 `S` 中选择一个距离源顶点最小的顶点 `v`。
3. 将 `v` 添加到最短路径树中，并将其标记为已访问。
4. 更新与 `v` 相邻的所有顶点的距离。
5. 重复步骤 2-4，直到 `S` 为空。

**代码块：**

def dijkstra(graph, source):
    """
    Dijkstra算法查找从源顶点到所有其他顶点的最短路径。

    参数：
        graph: 图的邻接表表示
        source: 源顶点
    返回：
        distance: 从源顶点到所有其他顶点的最短距离
        previous: 从源顶点到所有其他顶点的最短路径中的前一个顶点
    """

    # 初始化
    distance = [float('inf')] * len(graph)
    previous = [None] * len(graph)
    distance[source] = 0

    # 创建一个包含所有顶点的集合
    S = set(graph.keys())

    # 主循环
    while S:
        # 选择距离源顶点最小的顶点
        u = min(S, key=lambda v: distance[v])

        # 将顶点添加到最短路径树中