构建哈夫曼树：最优二叉树与应用实例

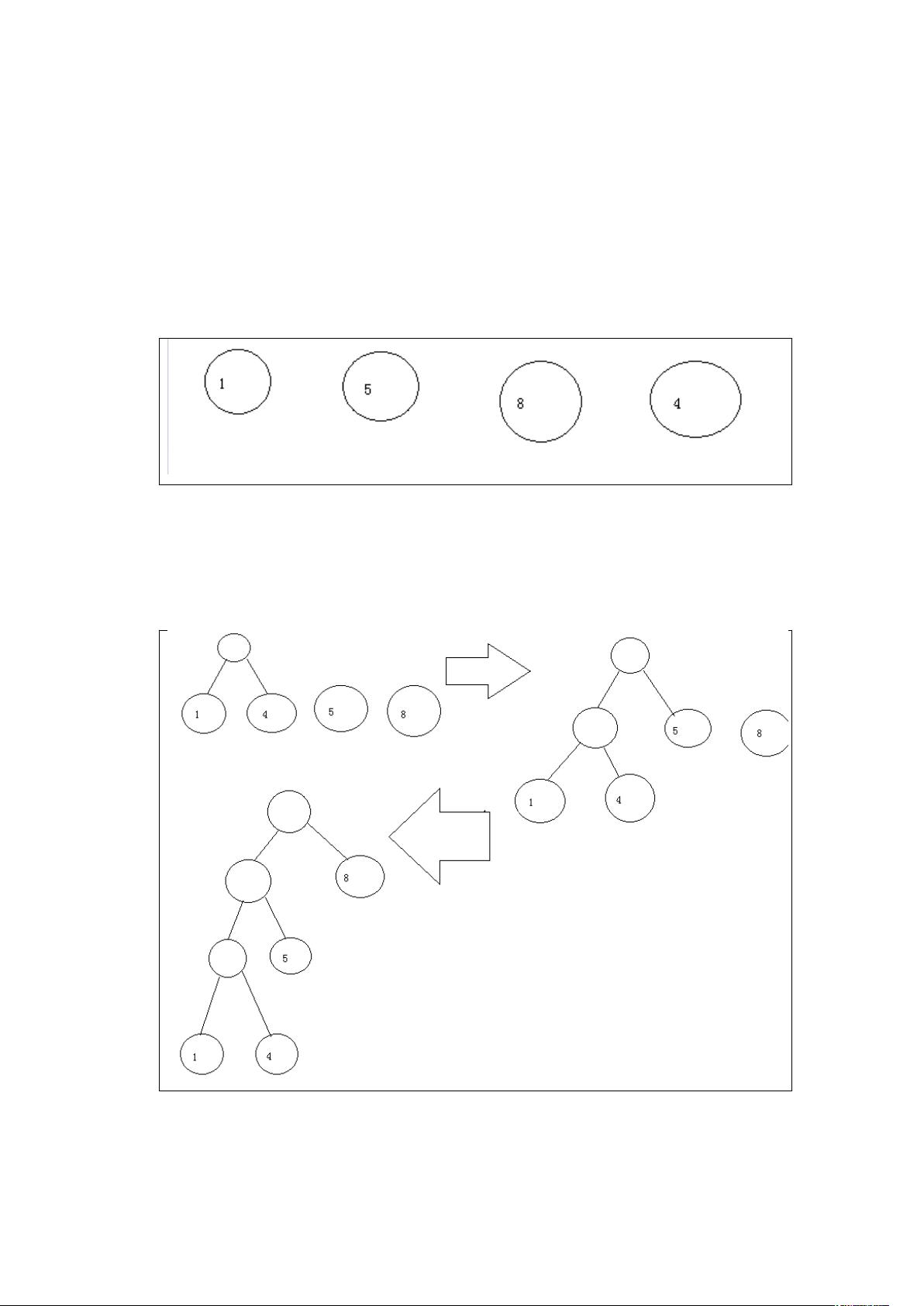
本篇Java基础复习笔记主要探讨了数据结构中的一个重要概念——哈夫曼树（Huffman Tree），也称为最优二叉树。哈夫曼树是一种特殊的二叉树，它的构建是基于带权重的节点，目的是找到具有最小加权路径长度的树。这里的权重指的是每个节点的值，而加权路径长度则是节点的权重乘以其在树中的路径长度。 首先，构建哈夫曼树的步骤如下： 1. 将所有带权重的节点按照权重从小到大进行排序。 2. 选取排序后的两个最小权重节点作为新父节点的子节点，形成一个新的节点，并更新剩余节点集合。 3. 重复步骤2，直到所有节点都被用于构建新的父节点，或者只剩下一个节点，此时剩下的节点就是哈夫曼树的叶子节点。 4. 使用广度优先搜索（BFS）遍历哈夫曼树，会得到从根节点到每个叶子节点的最短路径，即最短编码。 哈夫曼树的应用十分广泛，比如在Apache的负载均衡中，通过按权重分配请求来实现高效处理；在路由器的路由算法中，利用哈夫曼树优化数据包传输路径；在汉字点阵字形压缩存储中，哈夫曼树可以帮助减小存储空间；甚至在信息检索系统中，它可以用来实现快速查找。核心思想在于，当数据或信息具有权重和优先级时，哈夫曼树提供了一种有效的优化方法。 为了实现哈夫曼树，可以编写代码来模拟构建过程，如使用队列（ArrayDeque）和列表（ArrayList）来辅助操作。代码通常包括导入必要的库，如`java.util`，然后定义一个哈夫曼树类，包含创建树的方法，该方法按照上述步骤逐步构建。作者刘岩（liuyan）在代码注释中提供了自己的邮箱地址，表明这是一份个人的学习资料。 总结来说，这篇笔记重点介绍了哈夫曼树的构造方法，应用场景，以及如何在Java编程中实现这一数据结构。通过理解并掌握哈夫曼树，开发人员可以在实际项目中应用其优化数据结构和提高算法效率。