LCL型并网逆变器的实时双采样控制器设计与性能提升

connect

需积分: 10 93 浏览量更新于2024-07-21 收藏 1.64MB PDF 举报

身份认证购VIP最低享 7 折!

领优惠券(最高得80元）

资源详情

资源推荐

BAO et al.: STEP-BY-STEP CONTROLLER DESIGN FOR LCL-TYPE GRID-CONNECTED INVERTER 1241

is adopted to damp the resonance peak caused by the LCL ﬁl-

ter, and H

is the feedback coefﬁcient. Unipolar sinusoidal

pulsewidth modulation (SPWM) is used for the grid-connected

inverter. An outer-loop power control is usually introduced to

automatically adjust the current reference amplitude I

∗

.Thisis

beyond the scope of this paper and will not be discussed, and

the current reference amplitude I

∗

is directly given here.

The resonance frequency of the LCL ﬁlter f

is derived as

2π



+ L

. (1)

Fig. 1(b) shows the ASM of the LCL-type grid-connected in-

verter, where G

inv

is the transfer function of the inverter bridge.

The switching frequency of VSI is assumed to be sufﬁciently

high, thus G

inv

can be approximated as V

tri

, where V

the dc-link voltage and V

tri

is the amplitude of the triangle car-

rier wave. According to Mason’s gain formula [32], the injected

grid current i

can be derived as

(s)=

T (s)

1+T (s)

ref

(s) −

(s)

1+T (s)

(s)

= i

(s)+i

(s) (2)

where T (s) is the loop gain of the system and is expressed as

T (s)=

inv

(s)

C + s

inv

+ s (L

+ L

)

(3)

and G

(s) is expressed as

(s)=

C + sCG

inv

C + s

inv

+ s (L

+ L

)

. (4)

is related to the injected grid current reference i

ref

and i

is related to the grid voltage v

. i

and i

are expressed as

(s)=

T (s)

1+T (s)

ref

(s) (5)

(s)=−

(s)

1+T (s)

(s) . (6)

III. F

REQUENCY RESPONSES OF THE CURRENT REGULATOR

AND

CAPACITOR–CURRENT-FEEDBACK ACTIVE-DAMPING

According to (3), the bode diagram of the uncompensated

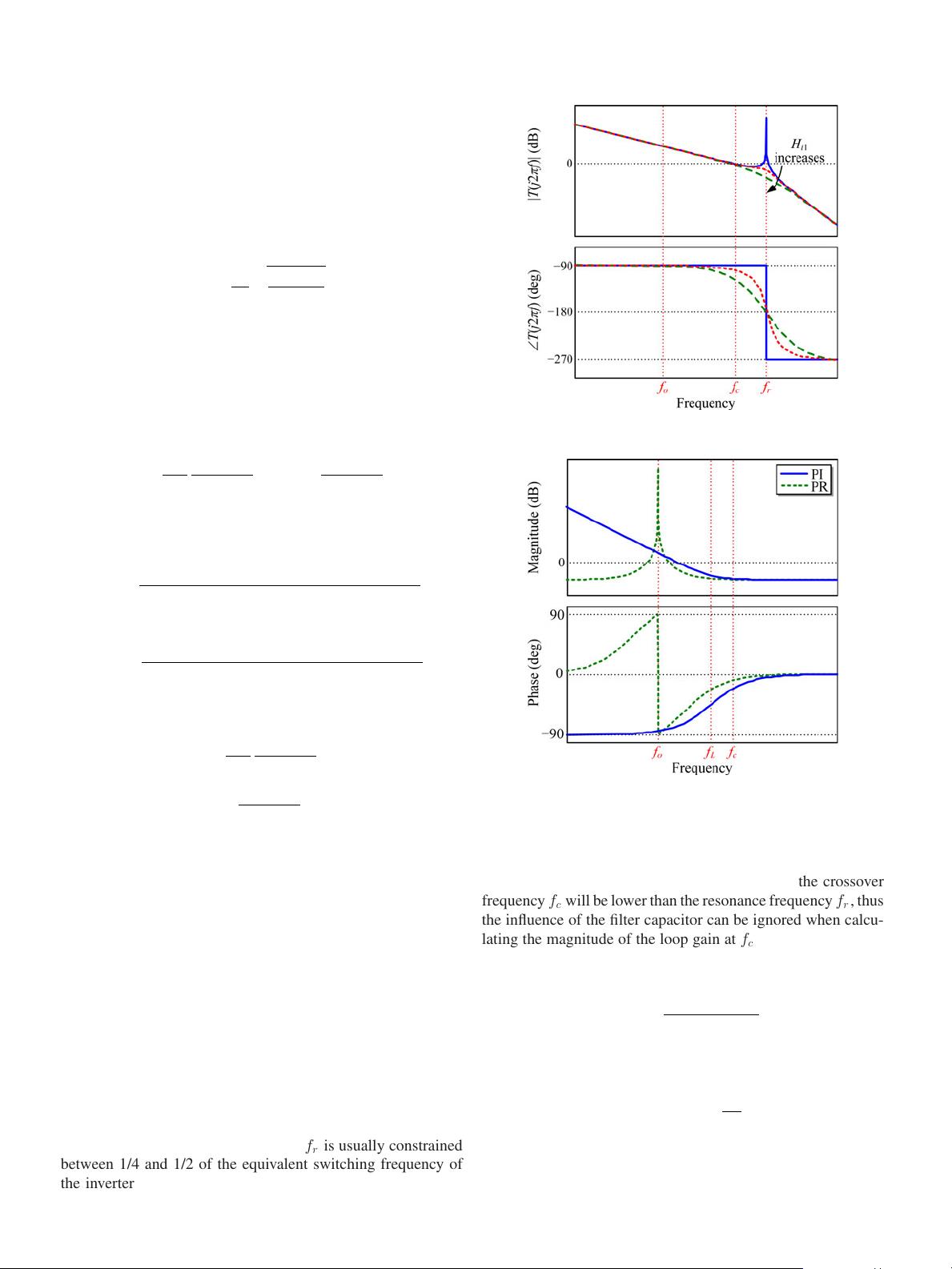
loop gain is depicted in Fig. 2. As seen, introducing the feedback

of the ﬁlter capacitor current can effectively damp the resonance

peak, and it only affects the magnitude of the loop gain at

the neighbor of the resonance frequency. However, this active-

damping method has signiﬁcant impact on the phase of the

loop gain and the phase decreases at the frequencies lower than

the resonance frequency. A larger capacitor–current feedback

coefﬁcient leads to better damping of the resonance peak, but

results in a larger negative phase shift.

The crossover frequency f

is typically restricted lower than

considering the effect of attenuating high-frequency noise,

where f

is the switching frequency of the inverter [9], and the

resonance frequency of the LCL ﬁlter f

is usually constrained

between 1/4 and 1/2 of the equivalent switching frequency of

the inverter (when unipolar SPWM is adopted, the equivalent

Fig. 2. Bode diagram of the loop gain without compensation.

Fig. 3. Bode diagram of PI and PR compensators.

switching frequency is 2f

), for the sake of effective harmonics

suppression and good dynamic response. Therefore, for a prop-

erly designed LCL-type grid-connected inverter, the crossover

frequency f

will be lower than the resonance frequency f

, thus

the inﬂuence of the ﬁlter capacitor can be ignored when calcu-

lating the magnitude of the loop gain at f

and the frequencies

lower than f

, i.e., the magnitude of T (s) can be approximated

|T (s)|≈



inv

(s)

s (L

+ L

)



. (7)

PI compensator is adopted as the injected grid current regu-

lator and the transfer function of G

(s) is given by

(s)=K

. (8)

According to (8), the bode diagram of PI compensator is

depicted in Fig. 3. As seen, at the frequencies around the corner

frequency f

which is expressed as f

= K

/(2πK

), the slope

剩余14页未读，继续阅读

mc470791823

粉丝: 1
资源: 3

LCL型并网逆变器的实时双采样控制器设计与性能提升

单相LCL并网逆变器.zip

LCL型并网逆变器的控制技术--阮新波

lcl型并网逆变器的控制技术

三相lcl型并网逆变器αβ轴仿真

lcl型并网逆变器的控制技术 pdf

lcl型并网逆变器的控制技术pdf

lcl并网逆变器simulink仿真 csdn

三相lcl并网逆变器仿真

单相lcl并网逆变器 csdn

lcl并网逆变器控制和电网电压定向控制的区别

三相lcl并网逆变器simulink仿真 csdn

单相lcl并网逆变器数学模型

南航trans复现: 电容电流前馈+电网电压全前馈_单相lcl并网逆变器仿真

三相并网逆变器滤波器LC型

三相并网逆变器lcl滤波器的参数设计与研究

三相并网逆变器的数学模型

lcl单相逆变器 simulink

lcl逆变器可以接负载么

simulink 单相并网lcl例程

最新资源