掌握线性系统时域分析关键要素与常用方法

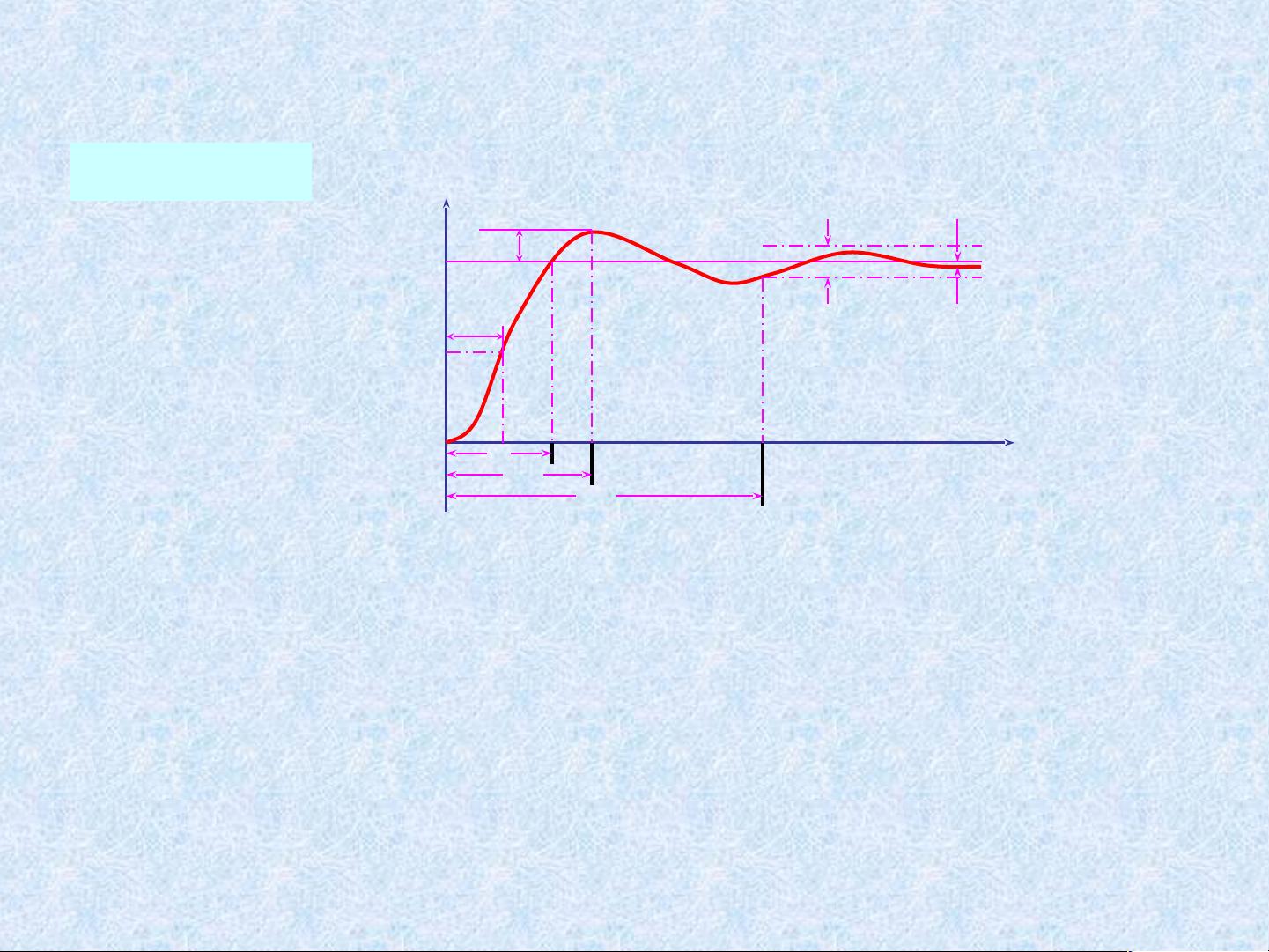
本章专注于线性系统的时域分析，这是经典控制理论中常用的一种工程分析方法，它主要研究系统在典型输入信号作用下的输出响应特性。时域分析法是通过对时间变量的研究，来了解系统从初始状态到稳定状态的过程，包括瞬态响应和稳态性能的分析。 首先，瞬态响应是系统在受到突然输入变化后，从非平衡状态过渡到平衡状态的过程，它是包含在输出响应中的短暂部分。对于一阶系统，其时域响应可以直观地理解为系统响应的上升时间和衰减速度；而对于二阶系统，由于具有阻尼和惯性效应，其响应更为复杂，通常涉及超调、衰减率和振荡次数等参数。 其次，系统稳定性是时域分析的重要内容。稳定性分析旨在判断系统是否能够从任何初始条件恢复到零状态，避免过度振荡或发散。通过计算系统的根轨迹或者研究系统特征方程的根分布，可以评估系统稳定性。 稳态性能分析关注的是当输入信号趋于无穷大或者输入信号停止变化后，系统的长期行为。这涉及到系统的稳态误差、调整时间等指标，反映了系统在静态工作条件下的性能。 经典时域分析通常使用一些典型输入信号进行，如阶跃函数、斜坡函数、抛物线函数、脉冲函数以及正弦函数。阶跃函数模拟了突变的输入，斜坡函数代表恒定速度的变化，这些信号有助于对比不同系统对相同输入的响应一致性。 拉普拉斯变换在这个过程中扮演着关键角色，它将时域中的线性常微分方程转换为复频域的代数方程，使得复杂问题简化处理。例如，阶跃函数和单位阶跃函数的拉普拉斯变换分别为1/s和1/s^2，这对于后续的系统分析提供了便利。 总结而言，线性系统的时域分析是控制理论基础中的核心内容，它通过研究系统的动态行为，帮助工程师理解和优化控制系统的性能，确保系统的稳定性和准确性。通过掌握这些基本概念和技术，可以为实际工程问题提供有效的解决方案。