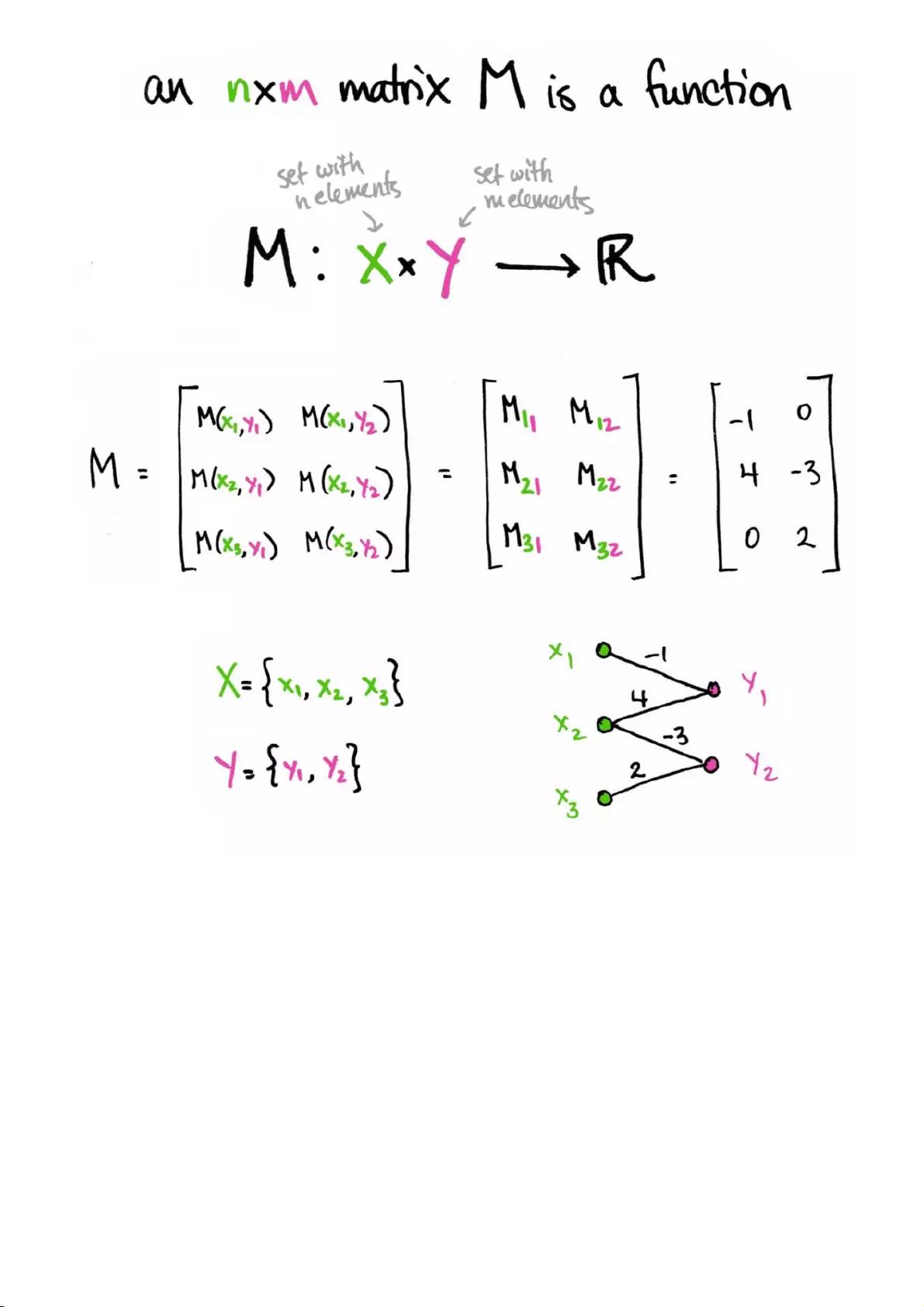矩阵与概率的可视化：将它们转化为加权二分图

"将矩阵和概率转化为图形的可视化方法" 在理解矩阵和概率的可视化之前，首先需要明确矩阵的基本概念。矩阵是由多个数按照特定排列组成的矩形阵列，通常用于表示线性变换、数据处理或其他数学操作。在这个可视化过程中，我们将矩阵视为一种特殊的函数，即矩阵M可以被看作是从集合X到集合Y的实值函数，记作M: X × Y → R。 在可视化的过程中，每个矩阵的行和列被映射为不同颜色的点。在例子中，矩阵的行对应于绿色点，列对应于粉色点。如果矩阵的某一个元素M_ij非零，那么就在代表i行的绿色点和代表j列的粉色点之间画一条线，并用该元素的值作为这条线的权重。如果M_ij为零，则不画线，表示这两点之间无连接。 这种可视化方法有助于我们直观地理解矩阵乘法。当两个矩阵M: X × Y → R和N: Y × Z → R可以相乘时，它们的图形可以组合在一起。新的矩阵MN的每个元素MN_ij表示从绿色的x_i点沿着原M矩阵的连线到粉色的y_j点，再沿着N矩阵的连线到蓝色的z_j点的所有路径的权重之积的总和。换句话说，对于MN的第ij项，我们需要找到所有从x_i出发，经过至少一个y_k点，最终到达z_j的路径，将这些路径上的M和N的相应连线权重相乘，然后将所有这些乘积相加。 这种可视化的价值在于它可以帮助我们直观地理解矩阵乘法的过程，尤其是在处理大型矩阵或涉及复杂关系时。例如，当我们处理概率分布时，可以将概率矩阵可视化为图，其中非零概率的连线表示事件之间的转移可能性。这样，我们可以更容易地识别模式、理解和解释数据。 此外，这种可视化方法还适用于其他数学概念，如概率图模型、图论问题和网络分析。在概率图模型中，节点可以代表随机变量，边则表示变量间的依赖关系。通过这种方式，我们可以直观地看到变量间的条件概率和联合概率结构。 将矩阵和概率转化为图形是一种强大的工具，它能帮助我们更好地理解抽象的数学概念，并将其应用到实际问题中。无论是教学、研究还是解决实际工程问题，这种方法都能提供有价值的洞察力。