复杂网络的结构与功能：Newman的经典综述

需积分: 10 94 浏览量更新于2024-08-02 1 收藏 819KB PDF 举报

"这篇经典文献综述由M.E.J.Newman撰写，主要探讨了复杂网络的结构和功能，包括互联网、社会网络、生物网络等实际系统的研究，以及一系列理解或预测这些系统行为的技术和模型。文章涵盖了小世界效应、度分布、聚类、网络关联、随机图模型、网络增长与优先附着模型以及网络上的动态过程等内容。" Newman的这篇文章是对复杂网络领域的重要贡献，他首先介绍了不同类型的网络，如社会网络、信息网络、技术网络和生物网络，这些网络在现实世界中扮演着关键角色。社会网络研究人际关系的结构，信息网络关注数据和信息的传输，技术网络涉及基础设施如电力和通信网络，而生物网络则涵盖了分子生物学中的相互作用网络，如蛋白质-蛋白质交互和基因调控网络。接着，Newman深入讨论了网络的特性，其中“小世界效应”是指尽管网络中节点间平均距离较长，但大多数节点都可以通过少数步骤到达的现象，这在网络效率和信息传播中至关重要。网络的“聚类”（transitivity or clustering）描述了节点之间的三元闭合，即朋友的朋友往往也是朋友，这种现象在社交网络中尤为明显。度分布是网络结构分析的关键，它描述了节点连接数量的分布情况。Newman特别提到了“无标度网络”，在这种网络中，节点的度分布遵循幂律，导致网络中存在大量低度节点和少量高度连接的节点（称为“中心节点”）。这种分布模式在许多真实网络中被观察到，如互联网和一些社会网络。此外，文章还讨论了随机图模型，如Erdős-Rényi模型，以及描述网络动态增长和演化的过程，如Barabási-Albert模型，该模型解释了网络中的“优先附着”现象，即新节点更倾向于连接到已有的高度连接节点，导致网络的无标度特征。最后，Newman简要介绍了发生在网络上的动态过程，如疾病传播、意见形成和信息扩散等，这些过程受网络结构的影响，进一步揭示了网络在现实世界中的复杂性和重要性。这篇综述提供了对复杂网络理论的全面概述，不仅阐述了基础概念，还介绍了相关模型和应用，对于理解复杂系统的结构和行为具有极大的价值。

network type n m z ` α C

(1)

(2)

r Ref(s).

social

ﬁlm actors undirected 449 913 25 516 482 113.43 3.48 2.3 0.20 0.78 0.208 20, 416

company directors undirected 7 673 55 392 14.44 4.60 – 0.59 0.88 0.276 105, 323

math coauthorship undirected 253 339 496 489 3.92 7.57 – 0.15 0.34 0.120 107, 182

physics coauthorship undirected 52 909 245 300 9.27 6.19 – 0.45 0.56 0.363 311, 313

biology coauthorship undirected 1 520 251 11 803 064 15.53 4.92 – 0.088 0.60 0.127 311, 313

telephone call graph undirected 47 000 000 80 000 000 3.16 2.1 8, 9

email messages directed 59 912 86 300 1.44 4.95 1.5/2.0 0.16 136

email address books directed 16 881 57 029 3.38 5.22 – 0.17 0.13 0.092 321

student relationships undirected 573 477 1.66 16.01 – 0.005 0.001 −0.029 45

sexual contacts undirected 2 810 3.2 265, 266

information

WWW nd.edu directed 269 504 1 497 135 5.55 11.27 2.1/2.4 0.11 0.29 −0.067 14, 34

WWW Altavista directed 203 549 046 2 130 000 000 10.46 16.18 2.1/2.7 74

citation network directed 783 339 6 716 198 8.57 3.0/– 351

Roget’s Thesaurus directed 1 022 5 103 4.99 4.87 – 0.13 0.15 0.157 244

word co-occurrence undirected 460 902 17 000 000 70.13 2.7 0.44 119, 157

technological

Internet undirected 10 697 31 992 5.98 3.31 2.5 0.035 0.39 −0.189 86, 148

power grid undirected 4 941 6 594 2.67 18.99 – 0.10 0.080 −0.003 416

train routes undirected 587 19 603 66.79 2.16 – 0.69 −0.033 366

software packages directed 1 439 1 723 1.20 2.42 1.6/1.4 0.070 0.082 −0.016 318

software classes directed 1 377 2 213 1.61 1.51 – 0.033 0.012 −0.119 395

electronic circuits undirected 24 097 53 248 4.34 11.05 3.0 0.010 0.030 −0.154 155

peer-to-peer network undirected 880 1 296 1.47 4.28 2.1 0.012 0.011 −0.366 6, 354

biological

metabolic network undirected 765 3 686 9.64 2.56 2.2 0.090 0.67 −0.240 214

protein interactions undirected 2 115 2 240 2.12 6.80 2.4 0.072 0.071 −0.156 212

marine food web directed 135 598 4.43 2.05 – 0.16 0.23 −0.263 204

freshwater food web directed 92 997 10.84 1.90 – 0.20 0.087 −0.326 272

neural network directed 307 2 359 7.68 3.97 – 0.18 0.28 −0.226 416, 421

TABLE II Basic statistics for a number of published networks. The properties measured are: type of graph, directed or undirected; total number of vertices n; total

number of edges m; mean degree z; mean vertex–vertex distance `; exponent α of degree distribution if the distribution follows a power law (or “–” if not; in/out-degree

exponents are given for directed graphs); clustering coeﬃcient C

(1)

from Eq. (3); clustering coeﬃcient C

(2)

from Eq. (6); and degree correlation coeﬃcient r, Sec. III.F.

The last column gives the citation(s) for the network in the bibliography. Blank entries indicate unavailable data.

III Properties of networks 11

The quantity ` can be measured for a network of n ver-

tices and m edges in time O(mn) using simple breadth-

ﬁrst search [7], also called a “burning algorithm” in the

physics literature. In Table II, we show values of ` taken

from the literature for a variety of diﬀerent networks. As

the table shows, the values are in all cases quite small—

much smaller than the number n of vertices, for instance.

The deﬁnition (1) of ` is problematic in networks that

have more than one component. In such cases, there

exist vertex pairs that have no connecting path. Con-

ventionally one assigns inﬁnite geodesic distance to such

pairs, but then the value of ` also becomes inﬁnite. To

avoid this problem one usually deﬁnes ` on such networks

to be the mean geodesic distance between all pairs that

have a connecting path. Pairs that fall in two diﬀerent

components are excluded from the average. The ﬁgures

in Table II were all calculated in this way. An alterna-

tive and perhaps more satisfactory approach is to deﬁne `

to be the “harmonic mean” geodesic distance between all

pairs, i.e., the reciprocal of the average of the reciprocals:

−1

n(n + 1)

i≥j

−1

. (2)

Inﬁnite values of d

then contribute nothing to the sum.

This approach has been adopted only occasionally in net-

work calculations [260], but perhaps should be used more

often.

The small-world eﬀect has obvious implications for the

dynamics of processes taking place on networks. For

example, if one considers the spread of information, or

indeed anything else, across a network, the small-world

eﬀect implies that that spread will be fast on most real-

world networks. If it takes only six steps for a rumor

to spread from any person to any other, for instance,

then the rumor will spread much faster than if it takes

a hundred steps, or a million. This aﬀects the number

of “hops” a packet must make to get from one computer

to another on the Internet, the number of legs of a jour-

ney for an air or train traveler, the time it takes for a

disease to spread throughout a population, and so forth.

The small-world eﬀect also underlies some well-known

parlor games, particularly the calculation of Erd˝os num-

bers [107] and Bacon numbers.

On the other hand, the small-world eﬀect is also math-

ematically obvious. If the number of vertices within a

distance r of a typical central vertex grows exponentially

with r—and this is true of many networks, including the

random graph (Sec. IV.A)—then the value of ` will in-

crease as log n. In recent years the term “small-world

eﬀect” has thus taken on a more precise meaning: net-

works are said to show the small-world eﬀect if the value

of ` scales logarithmically or slower with network size for

ﬁxed mean degree. Logarithmic scaling can be proved

http://www.cs.virginia.edu/oracle/

FIG. 5 Illustration of the deﬁnition of the clustering coeﬃ-

cient C, Eq. (3). This network has one triangle and eight

connected triples, and therefore has a clustering coeﬃcient of

3 × 1/8 =

. The individual vertices have local clustering

coeﬃcients, Eq. (5), of 1, 1,

, 0 and 0, for a mean value,

Eq. (6), of C =

for a variety of network models [61, 63, 88, 127, 164]

and has also been observed in various real-world net-

works [13, 312, 313]. Some networks have mean vertex–

vertex distances that increase slower than log n. Bollob´as

and Riordan [64] have shown that networks with power-

law degree distributions (Sec. III.C) have values of ` that

increase no faster than log n/ log log n (see also Ref. 164),

and Cohen and Havlin [95] have given arguments that

suggest that the actual variation may be slower even than

this.

B. Transitivity or clustering

A clear deviation from the behavior of the random

graph can be seen in the property of network transitivity,

sometimes also called clustering, although the latter term

also has another meaning in the study of networks (see

Sec. III.G) and so can be confusing. In many networks

it is found that if vertex A is connected to vertex B and

vertex B to vertex C, then there is a heightened proba-

bility that vertex A will also be connected to vertex C.

In the language of social networks, the friend of your

friend is likely also to be your friend. In terms of network

topology, transitivity means the presence of a heightened

number of triangles in the network—sets of three vertices

each of which is connected to each of the others. It can

be quantiﬁed by deﬁning a clustering coeﬃcient C thus:

C =

3× number of triangles in the network

number of connected triples of vertices

, (3)

where a “connected triple” means a single vertex with

edges running to an unordered pair of others (see Fig. 5).

In eﬀect, C measures the fraction of triples that have

their third edge ﬁlled in to complete the triangle. The

factor of three in the numerator accounts for the fact that

each triangle contributes to three triples and ensures that

C lies in the range 0 ≤ C ≤ 1. In simple terms, C is

the mean probability that two vertices that are network

neighbors of the same other vertex will themselves be

neighbors. It can also be written in the form

C =

6× number of triangles in the network

number of paths of length two

, (4)

12 The structure and function of complex networks

where a path of length two refers to a directed path start-

ing from a speciﬁed vertex. This deﬁnition shows that C

is also the mean probability that the friend of your friend

is also your friend.

The deﬁnition of C given here has been widely used

in the sociology literature, where it is referred to as the

“fraction of transitive triples.”

In the mathematical

and physical literature it seems to have been ﬁrst dis-

cussed by Barrat and Weigt [40].

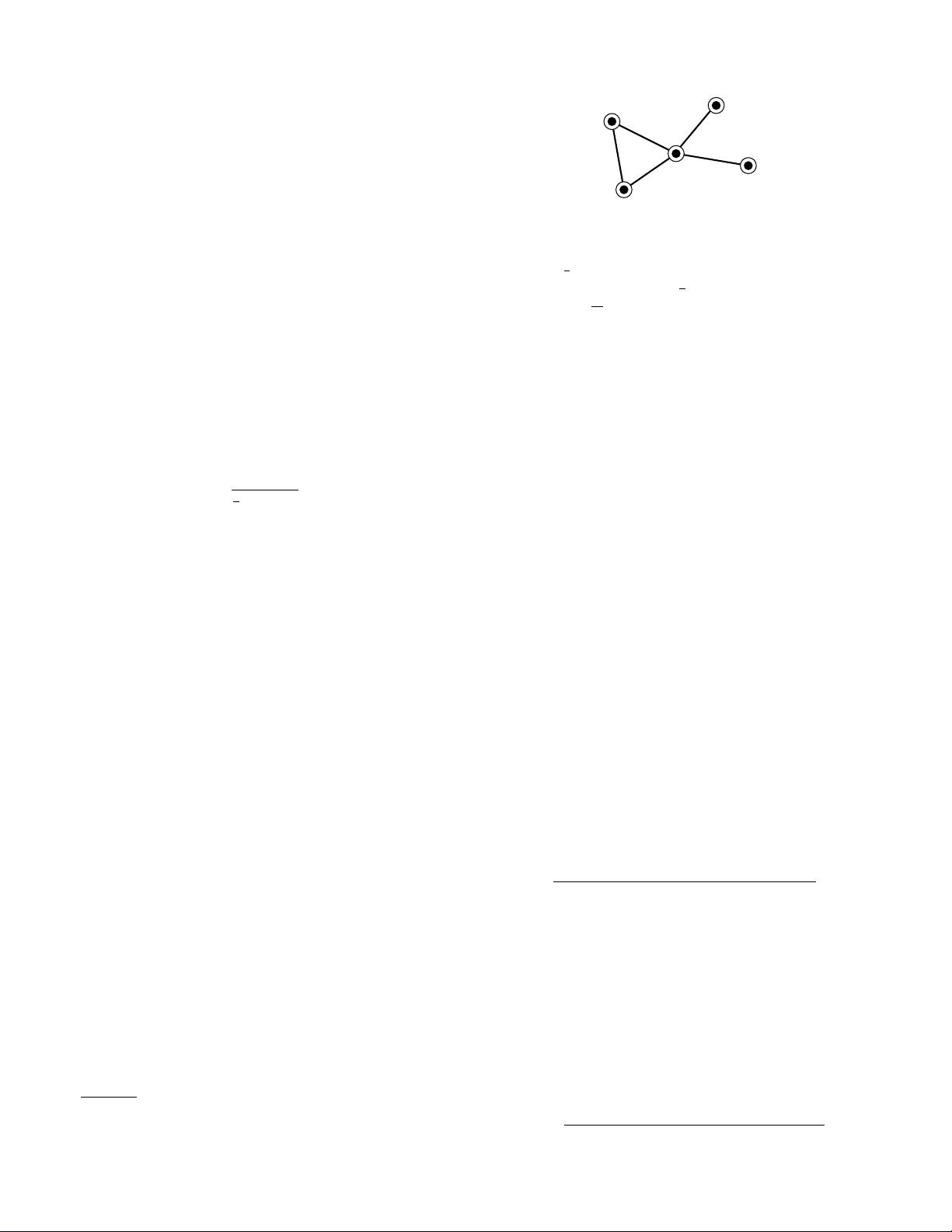
An alternative deﬁnition of the clustering coeﬃcient,

also widely used, has been given by Watts and Stro-

gatz [416], who proposed deﬁning a local value

number of triangles connected to vertex i

number of triples centered on vertex i

. (5)

For vertices with degree 0 or 1, for which both numerator

and denominator are zero, we put C

= 0. Then the

clustering coeﬃcient for the whole network is the average

C =

. (6)

This deﬁnition eﬀectively reverses the order of the oper-

ations of taking the ratio of triangles to triples and of

averaging over vertices—one here calculates the mean of

the ratio, rather than the ratio of the means. It tends

to weight the contributions of low-degree vertices more

heavily, because such vertices have a small denominator

in Eq. (5) and hence can give quite diﬀerent results from

Eq. (3). In Table II we give both measures for a number

of networks (denoted C

(1)

and C

(2)

in the table). Nor-

mally our ﬁrst deﬁnition (3) is easier to calculate analyt-

ically, but (6) is easily calculated on a computer and has

found wide use in numerical studies and data analysis. It

is important when reading (or writing) literature in this

area to be clear about which deﬁnition of the clustering

coeﬃcient is in use. The diﬀerence between the two is

illustrated in Fig. 5.

The local clustering C

above has been used quite

widely in its own right in the sociological literature,

where it is referred to as the “network density” [363].

Its dependence on the degree k

of the central ver-

tex i has been studied by Dorogovtsev et al. [113] and

Szab´o et al. [389]; both groups found that C

falls

oﬀ with k

approximately as k

−1

for certain models

of scale-free networks (Sec. III.C.1). Similar behavior

has also been observed empirically in real-world net-

works [349, 350, 397].

In general, regardless of which deﬁnition of the clus-

tering coeﬃcient is used, the values tend to be consid-

erably higher than for a random graph with a similar

number of vertices and edges. Indeed, it is suspected

that for many types of networks the probability that the

For example, the standard network analysis program UCInet in-

cludes a function to calculate this quantity for any network.

friend of your friend is also your friend should tend to

a non-zero limit as the network becomes large, so that

C = O(1) as n → ∞.

On the random graph, by con-

trast, C = O(n

−1

) for large n (either deﬁnition of C)

and hence the real-world and random graph values can

be expected to diﬀer by a factor of order n. This point

is discussed further in Sec. IV.A.

The clustering coeﬃcient measures the density of tri-

angles in a network. An obvious generalization is to ask

about the density of longer loops also: loops of length

four and above. A number of authors have looked at such

higher order clustering coeﬃcients [54, 79, 165, 172, 317],

although there is so far no clean theory, similar to a cu-

mulant expansion, that separates the independent contri-

butions of the various orders from one another. If more

than one edge is permitted between a pair of vertices,

then there is also a lower order clustering coeﬃcient that

describes the density of loops of length two. This coeﬃ-

cient is particularly important in directed graphs where

the two edges in question can point in opposite directions.

The probability that two vertices in a directed network

point to each other is called the reciprocity and is often

measured in directed social networks [363, 409]. It has

been examined occasionally in other contexts too, such as

the World Wide Web [3, 137] and email networks [321].

C. Degree distributions

Recall that the degree of a vertex in a network is the

number of edges incident on (i.e., connected to) that

vertex. We deﬁne p

to be the fraction of vertices in

the network that have degree k. Equivalently, p

is the

probability that a vertex chosen uniformly at random

has degree k. A plot of p

for any given network can

be formed by making a histogram of the degrees of ver-

tices. This histogram is the degree distribution for the

network. In a random graph of the type studied by Erd˝os

and R´enyi [141–143], each edge is present or absent with

equal probability, and hence the degree distribution is,

as mentioned earlier, binomial, or Poisson in the limit of

large graph size. Real-world networks are mostly found

to be very unlike the random graph in their degree dis-

tributions. Far from having a Poisson distribution, the

degrees of the vertices in most networks are highly right-

skewed, meaning that their distribution has a long right

tail of values that are far above the mean.

Measuring this tail is somewhat tricky. Although in

theory one just has to construct a histogram of the de-

grees, in practice one rarely has enough measurements to

get good statistics in the tail, and direct histograms are

thus usually rather noisy (see the histograms in Refs. 74,

An exception is scale-free networks with C

∼ k

−1

, as described

above. For such networks Eq. (3) tends to zero as n → ∞,

although Eq. (6) is still ﬁnite.

剩余57页未读，继续阅读

charlee_tao

粉丝: 0

复杂网络的结构与功能：Newman的经典综述

"斯坦福CS224W复杂网络分析：度分布、路径长度、聚类系数与连通组件

"斯坦福分析网络结构与社区发现

"斯坦福CS224W：复杂网络分析与构建方法

The structure and function of complex networks.pdf

The Structure and Function of Complex Networks 2003 Cite 5074 MEJ Newman.pdf

SOUND SOURCE LOCALIZATION BASED ON DEEP NEURAL NETWORKS WITH DIRECTIONAL ACTIVATE FUNCTION EXPLOITING PHASE INFORMATION

【Neural Network Expansion】: The Application of Neural Networks and Deep Learning Models in Linear ...

: Demystifying the Principles of Generative Adversarial Networks (GANs): Essential Basics and ...

The Role of MATLAB Genetic Algorithms in Complex System Modeling: Strategies and Case Studies

【Advanced Section】In-depth Study of Neural Networks: Deep Belief Networks and Adaptive Learning ...

最新资源