统计概念解析：方差、标准差与协方差

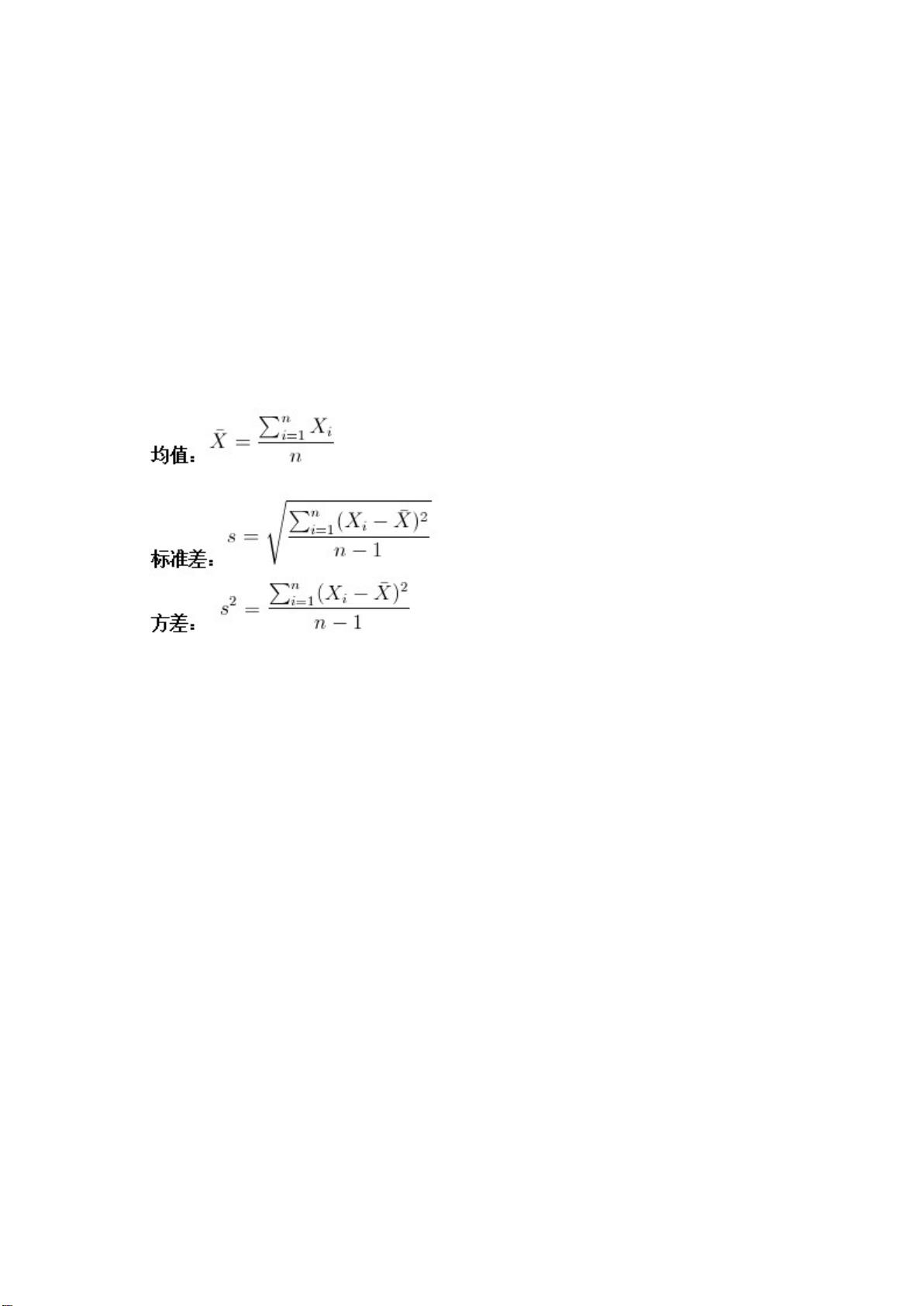
"这篇文章主要介绍了方差、标准差和协方差的概念，以及它们在多维数据中的应用。文中以两个具有相同均值但不同分布的集合为例，说明了标准差作为衡量数据散布度的重要性。此外，文章还探讨了协方差在度量两个随机变量相关性中的作用，以及协方差矩阵在处理高维数据时的应用。" 方差是衡量一组数据离散程度的重要统计量，它是每个数据点与均值之差的平方的平均数。标准差是方差的平方根，直观地表示数据点相对于均值的平均距离。在示例中，集合[0，8，12，20]和[8，9，11，12]虽然均值相同，但标准差的不同揭示了它们的分布差异，前者更分散。 协方差是用于分析两个随机变量之间线性关系的统计量。当两个变量的变化趋势一致，即同增或同减时，协方差为正；若两个变量的变化趋势相反，一个增加时另一个减少，协方差为负。如果协方差为零，则表明两个变量间不存在线性关系。通过协方差，我们可以推导出相关系数，它是一个归一化的指标，范围在-1到1之间，更便于比较不同尺度的变量之间的关系。 在多维数据中，协方差矩阵是一个非常有用的工具。对于n维数据集，协方差矩阵是对角线元素为各维度方差，非对角线元素为各维度间的协方差的对称矩阵。例如，一个三维数据集的协方差矩阵会包含三个自协方差（即每个维度的方差）和三个互协方差（表示不同维度之间的关系）。协方差矩阵的对角线元素对应于各维度内的方差，非对角线元素则表示不同维度之间的协方差。 在实际应用中，例如在Matlab中，可以使用内置函数计算协方差矩阵，这对于数据分析和建模工作至关重要。通过对协方差矩阵进行特征值分解或奇异值分解，可以进一步了解数据的结构，例如主成分分析（PCA）就是基于这一原理。 方差、标准差和协方差是统计分析中的基础工具，它们帮助我们理解数据的集中趋势和变异程度，以及不同变量间的相互关系。在处理高维数据时，协方差矩阵提供了一种有效的方式来捕捉多变量之间的复杂关系。理解和熟练运用这些概念，对于进行有效的数据分析和预测模型构建具有重要意义。