Catalan数的组合模型与推导方法探究

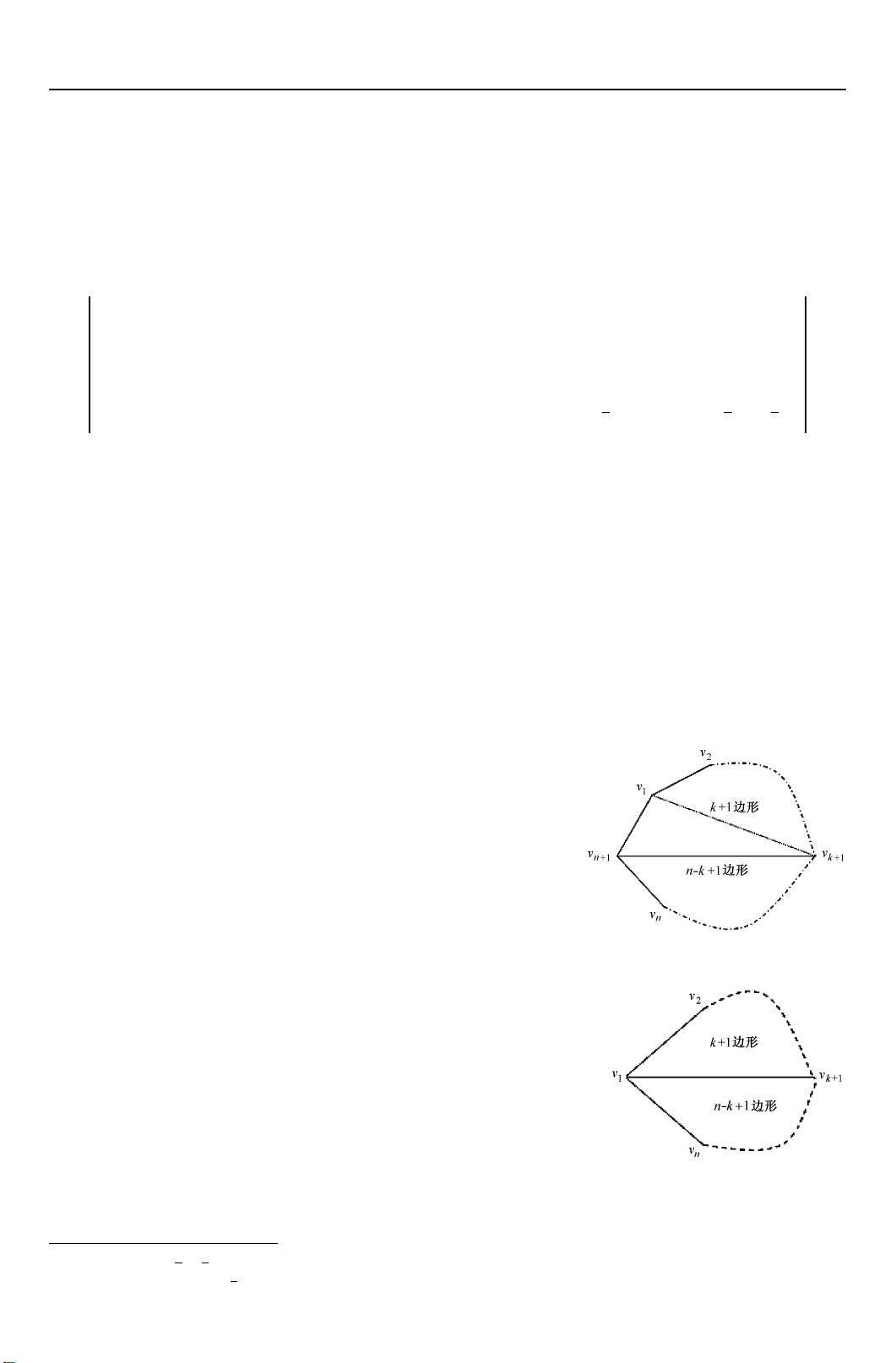
"这篇论文详细探讨了与Catalan数相关的组合问题，涵盖了Catalan数的四个经典组合模型和四种推导方法。作者赵天玉是组合数学领域的专家，他在文中介绍了Catalan数的历史背景，以及其在中国数学史上的先驱性发现。Catalan数在解决组合问题、路径问题、幂级数展开和不定方程解的计数等方面具有重要意义。" 在组合数学中，Catalan数是一类重要的计数函数，最早由E.Catalan在1838年提出，但实际上，Euler和中国的明安图更早地研究了这一概念。Catalan数的四个经典组合模型包括： 1. 凸多边形的三角剖分问题：给定一个凸n+1边形，可以画出n-2条两两不相交的对角线来分割成n-1个三角形。这种剖分的数量记为An，即Catalan数的一个实例。 2. 简单有序根树的计数问题：简单有序根树是一种特殊的树形结构，每个节点有0或1个子节点，且所有节点按某种顺序排列。这种树的数量也是Catalan数。 3. 路径问题：在二维平面上，从点(0,0)到点(n,n)的路径，要求路径只向右或向上移动，且不穿过对角线y=x。满足条件的不同路径数对应于Catalan数。 4. 乘法结合方式问题：在乘法运算中，有n+1个因子，它们可以通过不同的括号组合表示不同的乘法规则。例如，(a*(b*c))*(d*e)和(a*b)*(c*(d*e))是两种不同的组合方式。所有可能的组合方式数是Catalan数。 为了计算Catalan数，论文中介绍了四种方法： 1. 迭代递推方法：Catalan数满足递推关系C_n = Σ_{i=0}^{n-1} C_i * C_{n-i-1}，其中C_0 = 1。 2. 生成函数方法：通过Catalan数的生成函数C(x) = 1/(1 - x - x^2)，可以计算任意n的Catalan数。 3. 组合求差方法：利用其他序列的求和公式，通过差分运算得到Catalan数。 4. 一一映射方法：建立Catalan数与其他组合结构的一一对应关系，如与二叉树、非交叉路径等的关系。 Catalan数在各种领域都有应用，例如在投票理论中的唱票问题、计算平面中的非交叉曲线数量，以及在解析组合学和图论中的问题。论文列举了相关文献中的Catalan数的性质，并深入探讨了这些模型和方法，为理解和应用Catalan数提供了全面的视角。