网络诱导延迟与数据包丢失下奇异马尔可夫跳变系统非脆弱H∞输出跟踪控制设计

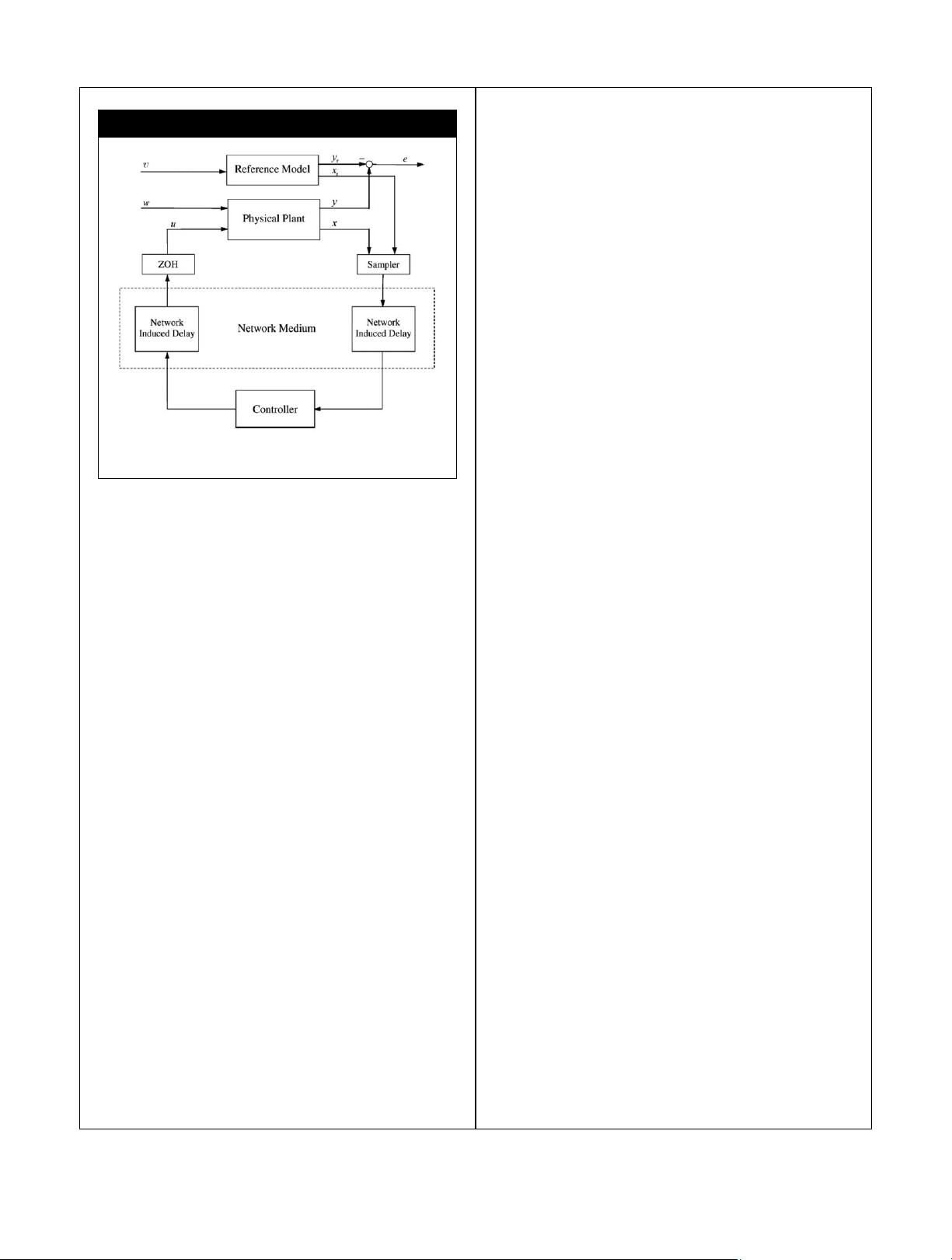
本文探讨的是在网络环境中具有不确定性、时变延迟和数据包丢失的奇异马尔可夫跳跃时滞系统中的非脆弱H1输出跟踪控制问题。研究的焦点在于设计一种针对系统状态的模式依赖型反馈控制器，该控制器能够在存在控制器增益扰动和有限的模式转换速率情况下，确保闭环网络控制系统输出能够精确追踪给定参考系统的输出，同时保持所需的H1输出跟踪性能。 首先，作者考虑的系统是奇异马尔可夫跳跃模型，这种模型的特点在于参数的随机性以及状态的非连续性，这增加了控制设计的复杂性。网络引入了额外的挑战，如信号传输延迟，这可能导致系统的实时性和稳定性受到威胁。数据包丢失进一步加剧了通信链路的不可靠性，使得控制算法必须具备鲁棒性，即使在数据不完整的情况下也能提供有效的控制性能。 本文的核心贡献是提出了一种新颖的控制策略，即非脆弱H1输出跟踪控制。非脆弱控制旨在确保系统在面对不确定性的同时，仍然能够维持预定的性能标准。通过构建一个多重随机Lyapunov-Krasovskii函数，研究人员能够设计出既能处理时滞效应又能处理数据丢失影响的控制器。这个函数不仅考虑了系统的动态特性，还包含了网络效应和不确定性的影响，从而使得控制设计更为全面和精确。 为了实现这一目标，文章可能涉及到以下步骤： 1. 建立系统的数学模型，包括状态方程、输出方程以及不确定性描述。 2. 设计状态反馈控制器的形式，通常会采用线性或近似线性化的方法。 3. 利用Lyapunov稳定性理论和小信号分析，确定控制器参数，确保闭环系统的稳定性。 4. 针对数据包丢失情况，可能采用概率模型或者统计方法来量化其对系统性能的影响，并在控制器设计中予以补偿。 5. 提出控制器的非脆弱性条件，即在控制器增益变化和模式转换速率限制下，输出跟踪性能依然能够满足预设的H1范数界限。 最后，该研究可能提供了数值仿真结果或者实验验证，以展示所设计控制器的有效性和鲁棒性。这篇研究对于理解和解决实际工业过程中的网络控制系统设计问题，特别是在存在时滞和数据丢包的苛刻环境下，具有重要的理论价值和应用前景。