实验十二:最小生成树(贪心算法)报告
2017061111 李静娴
1.问题描述
设 G=(V,E)是无向连通带权图,即一个网络。E 中每条边(v,w)的权为 c[v][w]。如果 G 的子
图 G’是一棵包含 G 的所有顶点的树,则称 G’为 G 的生成树。生成树上各边权的总和称为该
生成树的耗费。在 G 的所有生成树中,耗费最小的生成树称为 G 的最小生成树。
网络的最小生成树在实际中有广泛应用。例如,在设计通信网络时,用图的顶点表示城
市,用边(v,w)的权 c[v][w]表示建立城市 v 和城市 w 之间的通信线路所需的费用,则最小生
成树就给出了建立通信网络的最经济的方案。
2.实验目的
(1)熟悉贪心算法,并学以致用
(2)熟练掌握最小生成树算法
3.实验原理
1、MST 性质
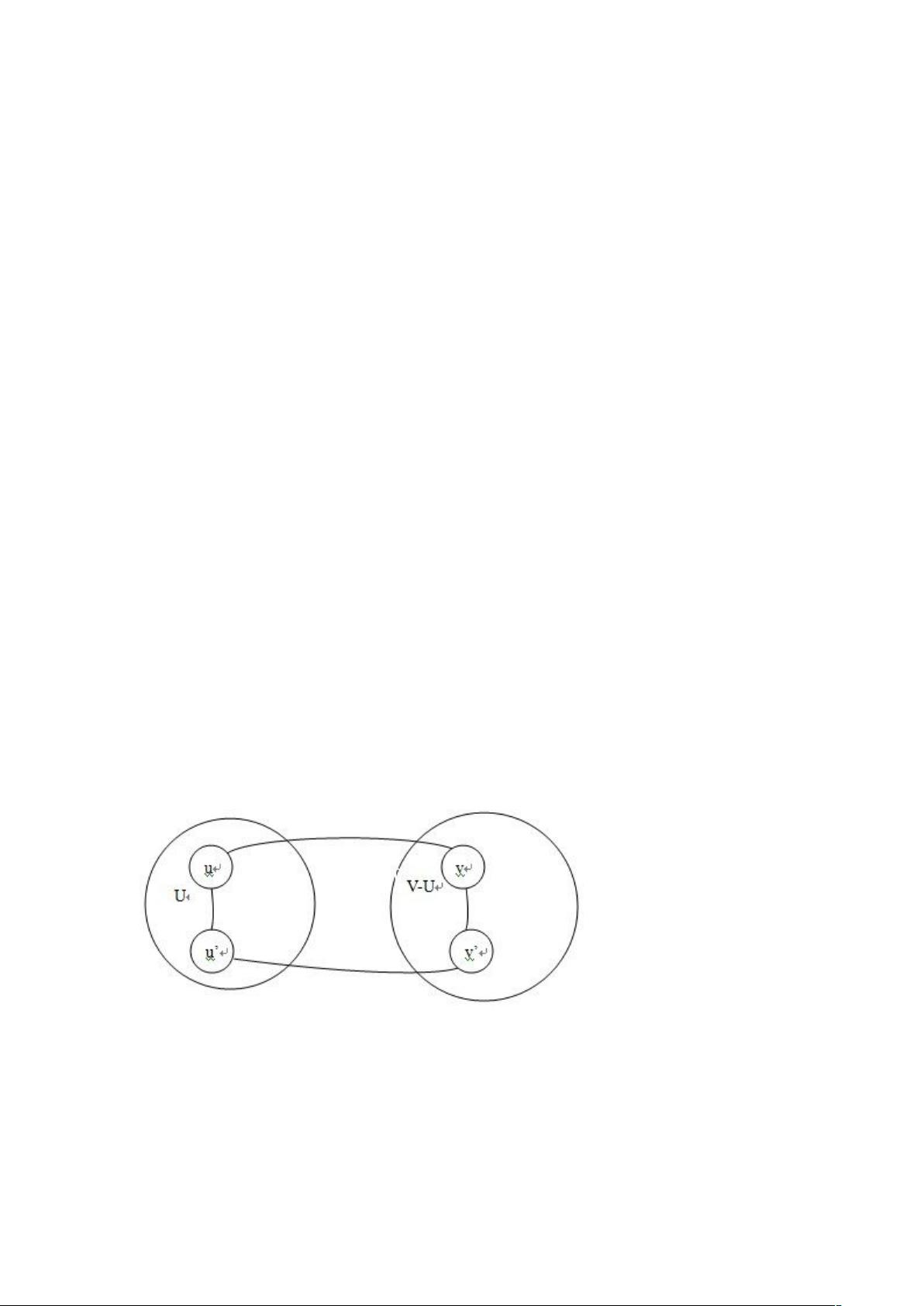
设 G=(V,E)是连通带权图,U 是 V 的真子集。如果(u,v)ÎE,且 uÎU,vÎV-U,且在所有这样的
边中,(u,v)的权 c[u][v]最小,那么一定存在 G 的一棵最小生成树,它以(u,v)为其中一条边。
这个性质有时也称为 MST 性质。|
MST 性质的证明:如图所示,假设 G 的任何一颗最小生成树都不包含边(u,v)。将边(u,v)
添加到 G 的一颗最小生成树 T 上,将产生含有边(u,v)的圈,并且在这个圈上有一条不同于
(u,v)的边(u',v'),使得 u'ÎU,v‘ÎV-U。将边(u',v')删去,得到 G 的另一颗生成树 T'。由于 c[u]
[v]<=c[u'][v'],所以 T'的耗费<=T 的耗费。于是 T'是一颗含有边(u,v)的最小生成树,这与假设
矛盾。
2、Prim 算法
设 G=(V,E)是连通带权图,V={1,2,…,n}。构造 G 的最小生成树的 Prim 算法的基本思想是:
首先置 S={1},然后,只要 S 是 V 的真子集,就作如下的贪心选择:选取满足条件 iÎS,jÎV-
S,且 c[i][j]最小的边,将顶点 j 添加到 S 中。这个过程一直进行到 S=V 时为止。在这个过程
中选取到的所有边恰好构成 G 的一棵最小生成树。













评论0