Rijndael算法：抵抗攻击的对称密码体制分析

"本文主要探讨了Rijndael算法在对称密码体制中的抵抗攻击能力，包括其消除弱密钥特性以及对线性攻击和差分攻击的有效防御。此外，文章还介绍了对称密码体制的基本概念，如分组密码原理、数据加密标准（DES）和高级加密标准（AES），以及分组密码的设计原则和结构，特别是Feistel网络结构。" Rijndael算法是被广泛使用的高级加密标准（AES），它在设计时特别考虑了抵抗各种攻击的能力。首先，Rijndael成功地消除了DES中存在的弱密钥问题，这意味着即使攻击者知道部分密钥信息，也无法轻易地推断出完整密钥。同样，它也解决了IDEA（国际数据加密算法）中发现的弱密钥问题，进一步增强了算法的安全性。 Rijndael对线性攻击和差分攻击的抵抗力是其安全性的关键特征。线性攻击是一种利用密文和明文之间的线性关系来尝试还原密钥的策略，而差分攻击则是通过比较输入数据微小变化导致的密文差异来分析密钥。Rijndael的非线性和复杂的混淆与扩散过程使得这些攻击难以奏效。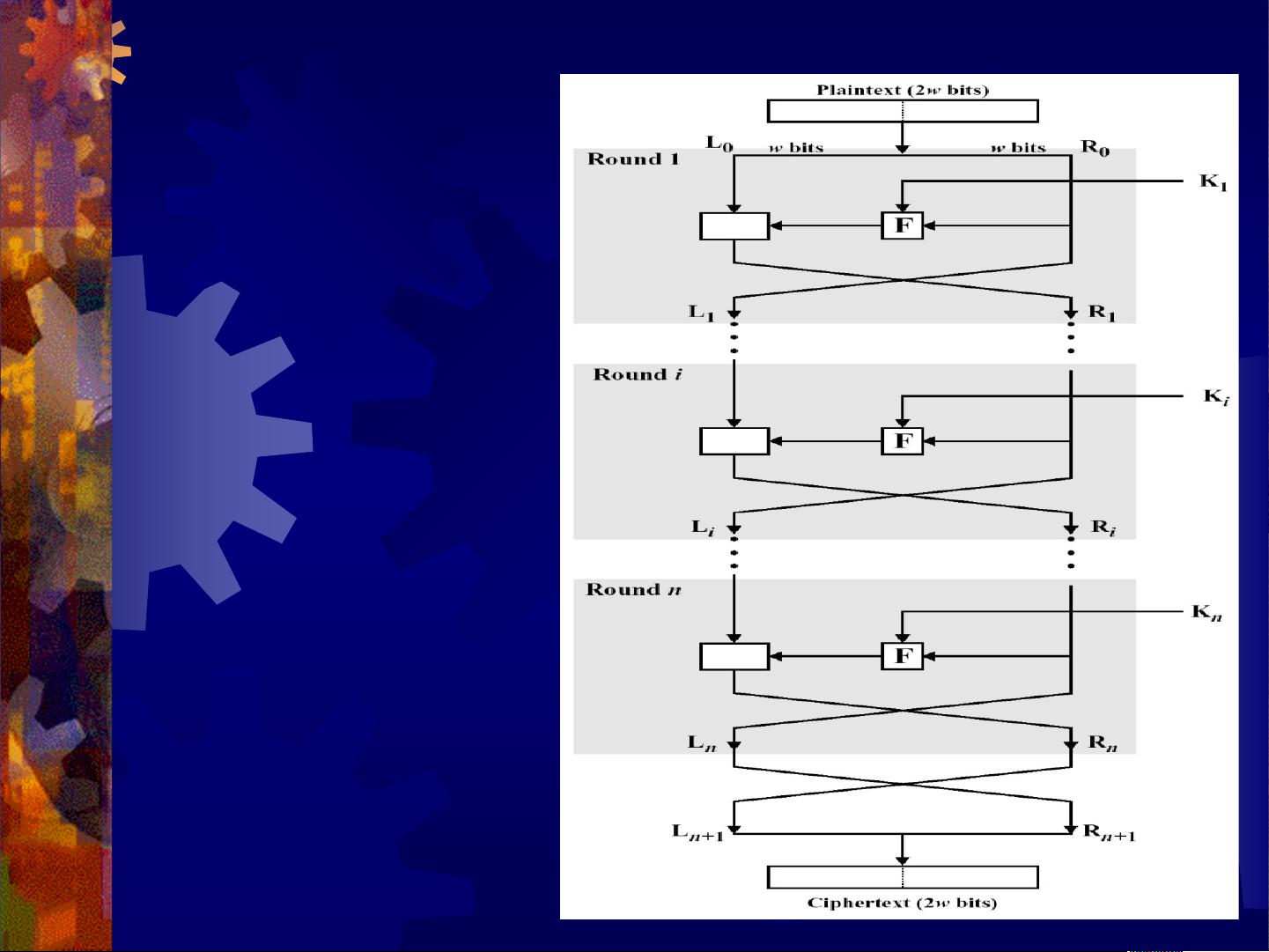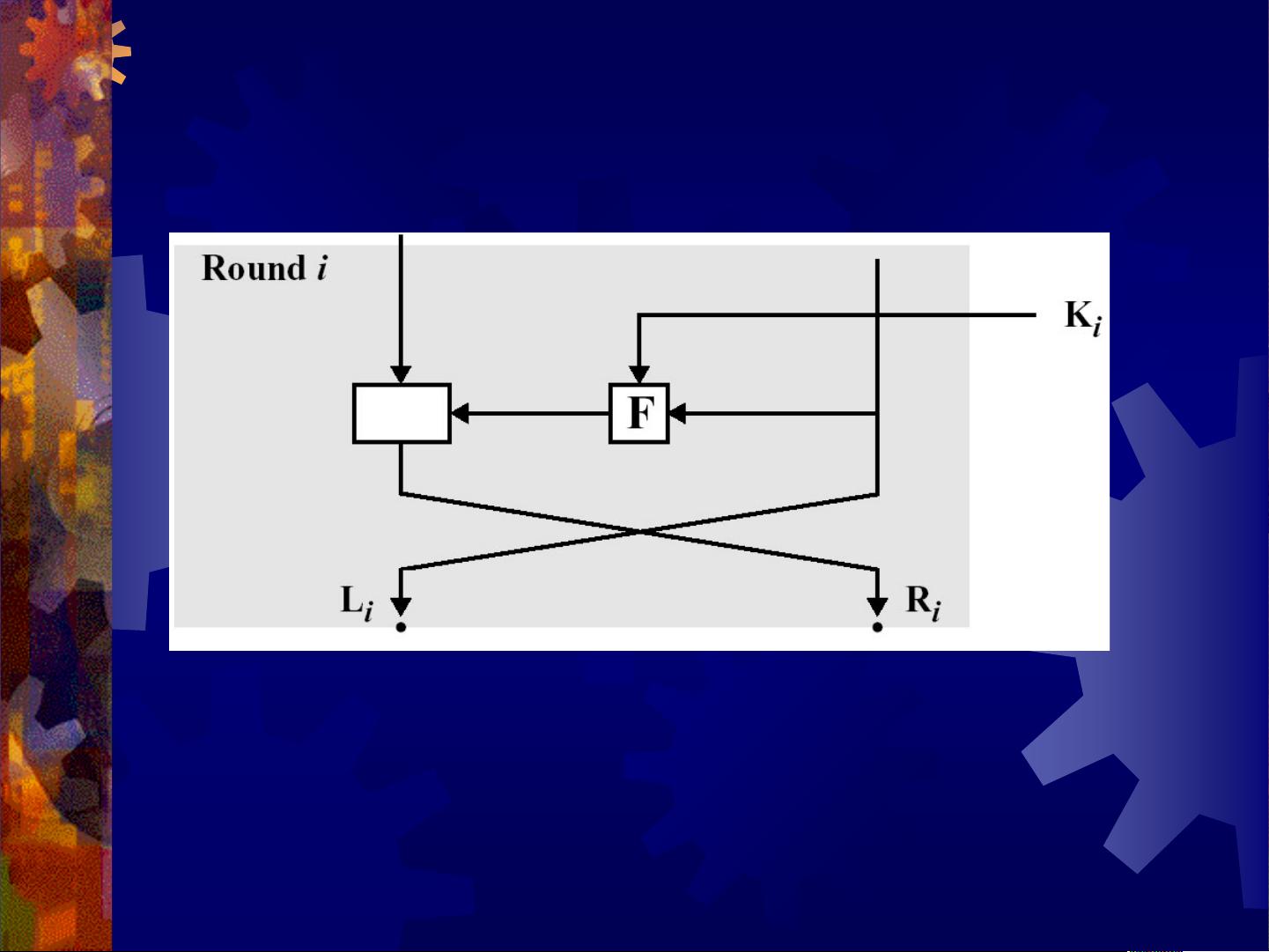 对称密码体制是密码学中的一种基础概念，它是指加密和解密使用同一密钥的加密方式。其中，分组密码是将大量明文数据分成固定长度的块进行加密，例如DES和AES。在分组密码中，Feistel结构是一种常见的设计模式，它通过一系列的替代和排列操作，实现了混淆和扩散，确保了加密过程的不可预测性。Feistel结构的特点是将数据块分为两半，每次迭代中对一半应用非对称函数，然后通过异或操作与另一半结合，这样保证了无论加密还是解密，步骤都是可逆的。 在Feistel结构中，替换（S-BOX）用于实现混淆，通过非线性函数使密钥和明文之间的关系变得复杂。排列（permutation）则负责扩散，确保明文的微小变化能够影响到密文的多个位置。这样的设计使得攻击者很难通过观察输出模式推断出输入信息，从而增加了破解的难度。 Rijndael算法通过精心设计的混淆和扩散机制，以及对DES和IDEA中弱密钥问题的解决，提供了强大的安全性。同时，其基于Feistel结构的分组密码设计也确保了算法的高效性和可逆性，使其成为现代加密技术的重要组成部分。