广度优先搜索BFS在图遍历中的应用与实现
需积分: 0 143 浏览量
更新于2024-08-05
收藏 5.14MB PDF 举报
"06D 广度优先搜索 BFS1 - 数据结构邓神 - 化繁为简"
在图论和算法领域,广度优先搜索(Breadth-First Search,简称BFS)是一种用于遍历或搜索树或图的算法。这种算法从根节点开始,然后遍历所有相邻节点,再对每个相邻节点进行相同的操作,直到遍历完所有节点。BFS的核心思想是使用队列数据结构来存储待访问的节点,确保先访问距离起点近的节点,再访问远的节点。
在处理树时,我们可以通过遍历将其转换为序列,即从半线性结构变为线性结构。同样,对于图,我们也需要一种方法将其转换,以便更方便地操作。BFS正是这样的工具,它将图转换为一棵无环的树,这棵树被称为支撑树(Spanning Tree)。支撑树的特点是包含了原图的所有顶点,但没有环路,因此它实际上是一个树形结构。
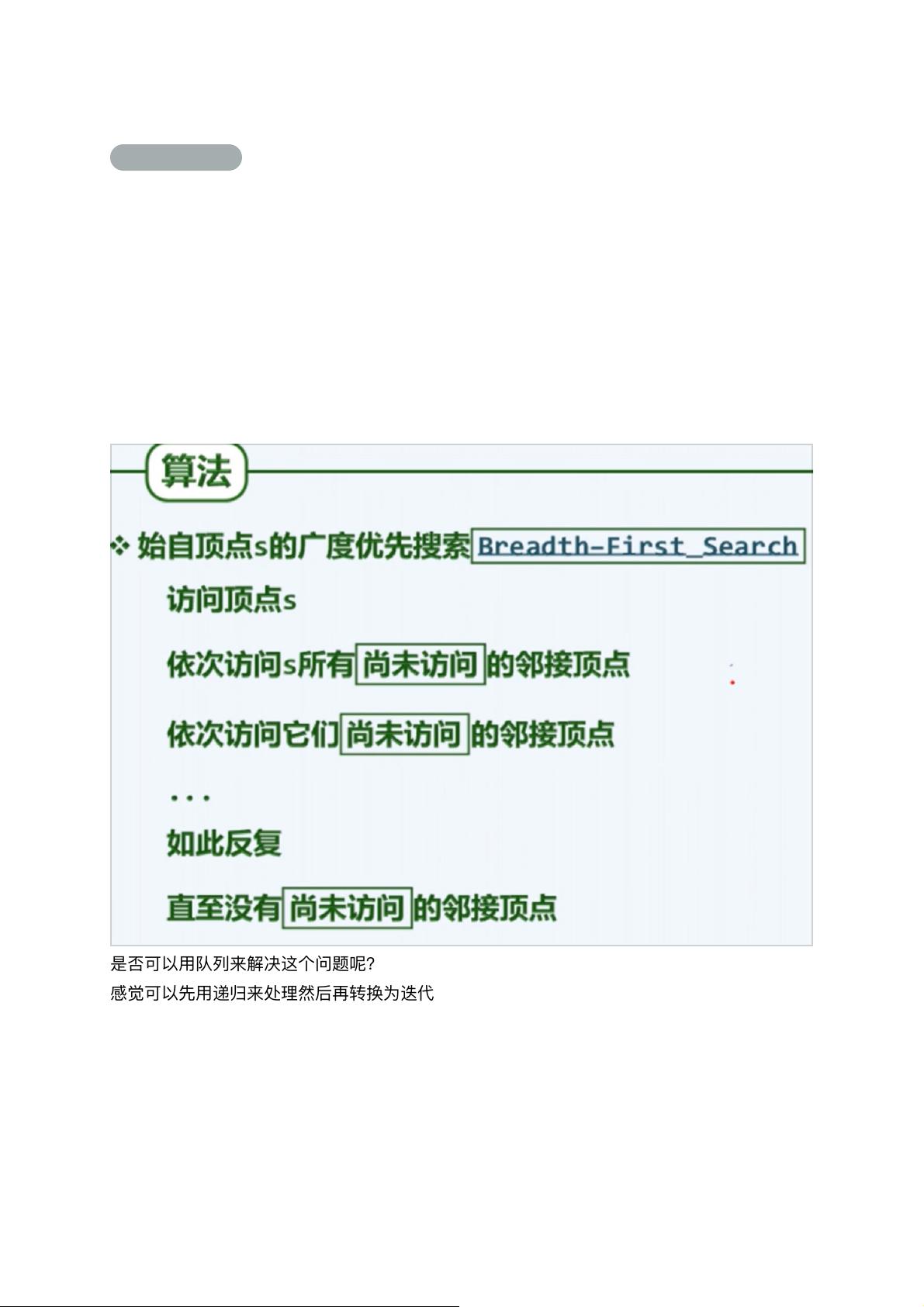
BFS算法的基本步骤如下:
1. 初始化:设置一个队列,将起始节点标记为已发现(DISCOVERED),并将其入队。
2. 循环:只要队列不为空,就执行以下操作:
- 取出队首节点,为其分配时间戳(dTime),表示该节点被访问的时间。
- 遍历当前节点的所有邻居:
- 如果邻居尚未被发现(状态为UNDISCOVERED),则标记其为已发现,将其入队,并设置与当前节点之间的边为支撑树的边(BFSTREE),同时记录当前节点为邻居的父节点。
- 如果邻居已经被发现(状态为DISCOVERED或VISITED),则根据不同的情况处理边的状态,如设置为交叉边(CROSS)或回边(BACK)。
这里的代码实现使用了模板,适用于任何类型的数据(Tv表示节点值类型,Te表示边的类型)。`Graph<Tv, Te>::BFS`函数接收一个起始节点和一个时间参数(clock),用队列(Q)来存储待访问的节点。在循环中,首先检查队列是否为空,然后取出队首节点,更新其时间戳,接着遍历其邻居并根据状态进行相应的处理。
BFS的应用广泛,例如在寻找最短路径、检测连通性、查找最近的节点等问题中都有所应用。由于它优先处理离起点近的节点,所以在寻找最短路径时(特别是在所有边权重相等的情况下),BFS是有效的解决方案。同时,BFS在社交网络分析、网络路由和游戏AI等领域也有着重要作用。
2022-01-04 上传
2022-05-01 上传
2023-06-06 上传
2023-03-07 上传
2023-05-25 上传
2023-08-08 上传
2023-12-07 上传
2023-05-28 上传
2023-05-26 上传
稚气筱筱
- 粉丝: 19
- 资源: 320
最新资源
- MATLAB实现小波阈值去噪:Visushrink硬软算法对比
- 易语言实现画板图像缩放功能教程
- 大模型推荐系统: 优化算法与模型压缩技术
- Stancy: 静态文件驱动的简单RESTful API与前端框架集成
- 掌握Java全文搜索:深入Apache Lucene开源系统
- 19计应19田超的Python7-1试题整理
- 易语言实现多线程网络时间同步源码解析
- 人工智能大模型学习与实践指南
- 掌握Markdown:从基础到高级技巧解析
- JS-PizzaStore: JS应用程序模拟披萨递送服务
- CAMV开源XML编辑器:编辑、验证、设计及架构工具集
- 医学免疫学情景化自动生成考题系统
- 易语言实现多语言界面编程教程
- MATLAB实现16种回归算法在数据挖掘中的应用
- ***内容构建指南:深入HTML与LaTeX
- Python实现维基百科“历史上的今天”数据抓取教程