有限容量Geom/Geom/1离散时间排队系统分析

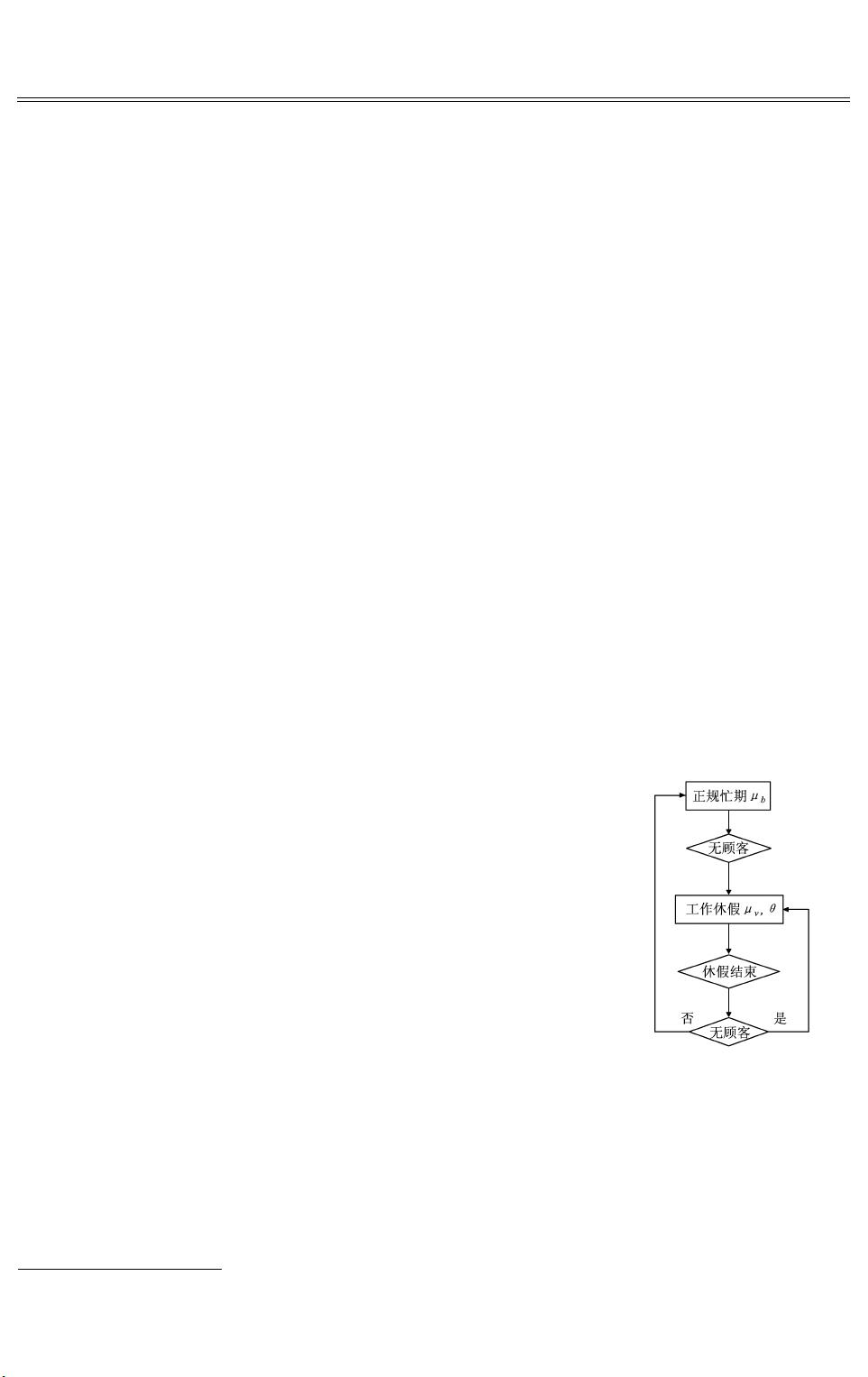
"这篇论文是关于有限容量的离散时间排队系统，具体是Geom/Geom/1多重工作休假模型。研究中，系统容量设定为N，当达到满载时，新到的顾客会自动消失。作者们构建了状态转移概率矩阵，并通过求解有限方程组来分析系统在稳定状态下的队长分布。进一步，他们利用这些结果得到了稳定状态下顾客消失的概率、队长的生成函数（PGF）、平均队长以及顾客等待时间的生成函数。该研究属于运筹学领域，特别关注离散时间排队理论和有限容量系统，对于理解和优化计算机网络等实际应用有重要意义。" 在离散时间排队理论中，有限容量的系统模型考虑了系统容量限制对服务过程的影响。在本文所探讨的Geom/Geom/1/MWV模型中，"Geom"代表服务时间和顾客到达时间都遵循几何分布，而"MWV"则指的是多重工作休假机制，意味着服务员在完成一定服务后会有休息时段。这种模型更贴近现实情况，例如在客户服务或生产环境中，员工可能会有多个班次或者休息时间。 论文首先建立了系统模型，其中顾客到达遵循几何分布，服务时间同样如此。到达间隔的概率由参数p决定，即P(A=k) = p(1-p)^{k-1}，k>=1，其中0<p<1。服务时间的概率分布也是类似的。当系统达到其最大容量N时，新到的顾客不再加入队列，而是直接消失，这是一个重要的特性，使得系统在容量限制下运行。 接着，作者通过建立状态转移概率矩阵来描述系统在不同状态之间的转换。这个矩阵包含了系统从一种状态转移到另一种状态的可能性，是分析离散时间排队系统的关键工具。通过解决与这个矩阵相关的有限方程组，可以得到系统的稳态特性。 论文的主要成果之一是得到了稳态下系统队长的分布。队长分布提供了关于系统中平均顾客数量的信息，这对于理解系统的性能指标至关重要。此外，队长的生成函数（Probability Generating Function, PGF）可以帮助计算各种队长统计量，如期望值和方差。 除了队长分布，作者还计算了稳定状态下顾客消失的概率，这反映了系统的服务能力以及顾客在系统中的流动性。同时，他们也得到了顾客等待时间的PGF，这能揭示顾客平均等待时间的分布，对于服务质量评估和系统优化至关重要。 最后，平均队长和顾客等待时间的计算是优化排队系统效率的重要参考。这些数值可以帮助决策者确定是否需要增加系统容量、调整服务速度或改变顾客到达率以提高整体效率。 这篇2011年的论文深入研究了有限容量的离散时间排队系统，特别是Geom/Geom/1/MWV模型，提供了理论分析和计算方法，对于理解和改进实际中的排队系统具有很高的学术价值和实践意义。