高速模(2n-2p-1)乘法器设计：TDM压缩树与负数修正优化

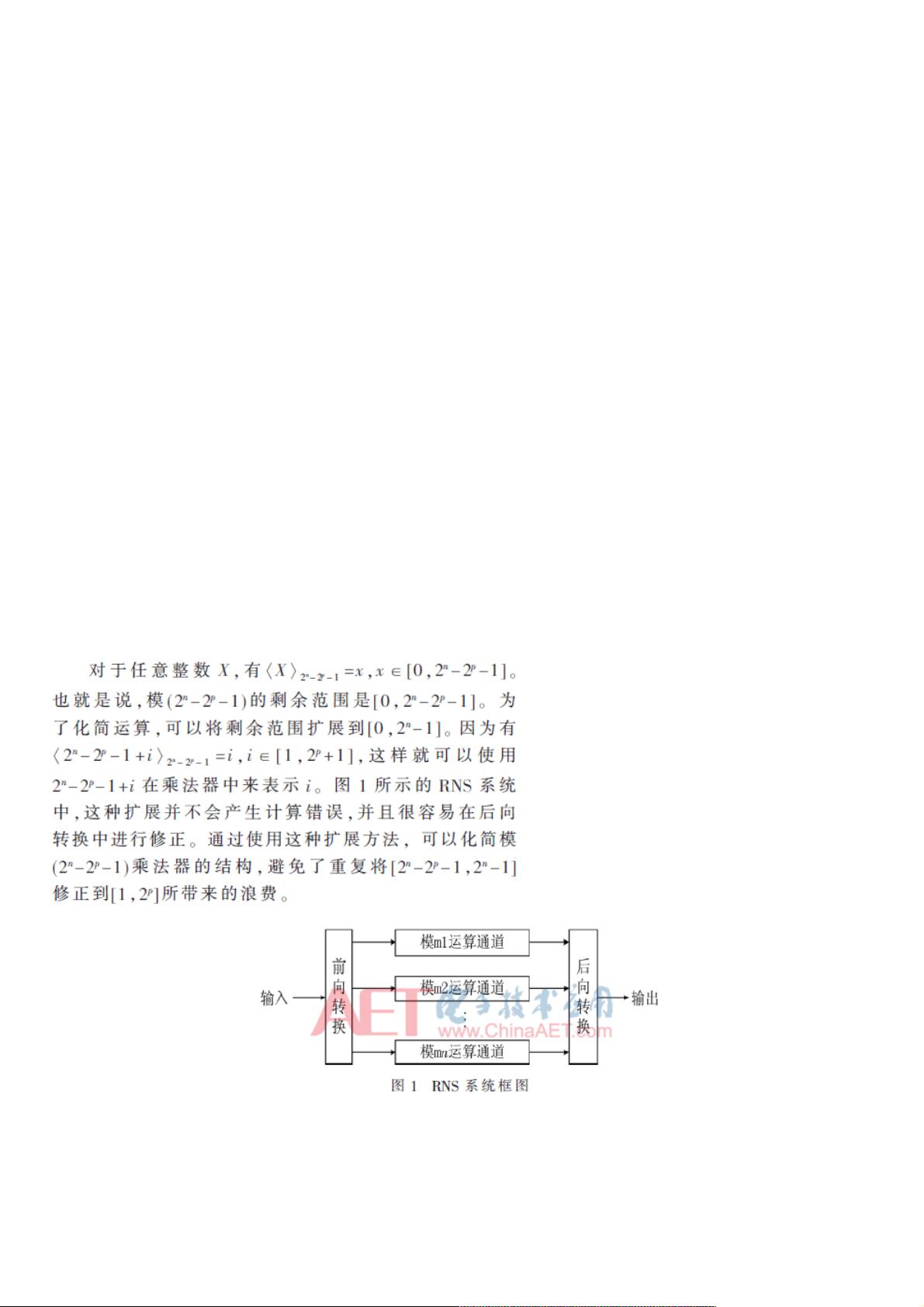
"本文主要介绍了一种高速模(2n-2p-1)乘法器的设计，利用余数系统和新型部分积压缩树优化了传统模乘法器的性能，减少了延迟并解决了Booth编码带来的负数修正问题。通过剩余范围的扩展，将模乘法器的效率显著提升，尤其在90纳米工艺下，与现有模(2n-2p-1)乘法器相比，延迟性能提高了10.4%至49%。设计的核心包括TDM压缩树算法的应用和对Booth编码问题的规避。" 在数字信号处理和计算领域，模乘法器是基础的运算单元，特别是在加密、解密、信号编码和大规模集成电路中发挥着重要作用。模(2n-2p-1)乘法器因其在剩余数系统(Remainder Number System, RNS)中的应用而备受关注，因为它可以形成高平衡度的基，简化计算过程。然而，传统的模乘法器设计通常存在延迟大和处理负数修正复杂的问题，这些问题在Booth编码模乘法器中尤为突出。 针对这一挑战，本文提出了一种创新的模(2n-2p-1)乘法器设计，它利用了剩余范围的扩展技术，将原有的范围[0, 2n-2p-1]扩展到[0, 2n-1]，这不仅简化了乘法器的结构，也为优化运算速度提供了空间。此外，文中引入了TDM压缩树算法，这是一种三维最小化算法，能够在不增加额外成本的情况下，有效缩短不同部分积之间的最大延迟路径，从而提高乘法器的速度。TDM算法支持使用4:2或其他形式的压缩器，以适应不同的布局布线需求，并能将部分积压缩至两行，进一步减少延迟。 该模(2n-2p-1)乘法器的设计摒弃了Booth编码，避免了负数修正的复杂性，这在处理无符号乘法时特别有利，因为余数系统中的乘法通常涉及较低位数的无符号数。通过这种方式，新设计的乘法器不仅提升了计算速度，还降低了负数修正带来的额外计算负担。 实验结果显示，采用90纳米工艺的该模乘法器相比于现有的模(2n-2p-1)乘法器，延迟性能提高了10.4%至49%，这是一个显著的性能提升。这一改进对于优化计算密集型应用，如密码学、大数据处理和高级通信系统，具有重要的实际意义。 本文的贡献在于提出了一种高速模(2n-2p-1)乘法器设计，结合了余数系统的优势和TDM压缩树算法的效率，解决了传统模乘法器存在的延迟和负数修正问题，为高性能计算硬件设计提供了新的思路。未来的研究可以进一步探索这种设计在不同工艺节点和应用场景下的性能表现，以及可能的优化策略。