MATLAB/Simulink在嵌入式鲁棒控制系统设计中的应用

需积分: 9 43 浏览量更新于2024-07-17 2 收藏 48.98MB PDF 举报

《使用MATLAB®/Simulink®设计嵌入式鲁棒控制系统》是一本由Petko Hristov Petkov、Tsonyo Nikolaev Slavov和Jordan Konstantinov Kralev合著的专业书籍，归属于"IETCONTROL, ROBOTICS AND SENSORS SERIES"第113卷。该书于2018年6月20日出版，共536页，详细介绍了在现代工业和自动化领域中，如何利用MATLAB®和Simulink®这两个强大的工具进行嵌入式控制系统的开发与设计。本书分为多个章节，旨在提供深入理解嵌入式控制系统的全面视角。首先，第1章概述了嵌入式控制系统的基本概念，强调了它们在实际应用中的重要性和挑战。接下来，第2章系统地介绍了系统建模的方法，包括线性系统理论和矩阵分析的基础元素，为后续控制器设计奠定基础。性能要求和设计限制在第3章被深入探讨，讨论了在实际环境中如何设定和满足控制系统的性能指标，同时考虑硬件限制和可靠性。第4章着重于控制器设计，涵盖了各种设计策略和技术，如H∞控制、滑模控制和模型预测控制等，以及如何利用MATLAB®/Simulink®工具箱进行仿真和优化。随后，书中通过三个案例研究（Case Study 1~3）展示了具体的设计应用：第1个是坦克物理模型的嵌入式控制，第2个是微型直升机的鲁棒控制，以及第3个是两轮机器人控制系统的优化。这些案例展示了如何将理论知识转化为实际工程实践。附录部分提供了额外的技术支持，包括矩阵分析、线性系统理论、随机过程、系统识别方法、IMU与目标微控制器接口技术，以及使用霍尔编码测量角度速度等实用技巧。这些内容对深入理解和解决实际问题至关重要。《Design of Embedded Robust Control Systems Using MATLAB®/Simulink®》是一本实用的参考书，适合控制工程、机器人学和传感器领域的研究人员、工程师，以及那些寻求使用MATLAB®和Simulink®进行复杂控制系统设计的实践者。通过阅读这本书，读者可以掌握从系统建模到实现鲁棒控制的完整流程，以及如何利用现代工具进行高效的设计和测试。

Preface xv

Acknowledgments

The authors are indebted to several people and institutions who helped them in the

preparation of the book. We are particularly grateful to The MathWorks, Inc. for

their continuous support, and to Professor Da Wei Gu from Leicester University, and

Professor Nicolai Christov from Université Lille 1 for the numerous discussions and

help. The assistance from IET editors and comments from the Reviewers are highly

appreciated. We are also very grateful to Professor Tasho Tashev, Dean of the English

Department of Engineering of the Technical University of Sofia, for his continuous

support of our work in the recent years.

Using downloadable material

As a supporting online material for this book, we present seven folders with more

than 250 .M- and .SLX-files intended for the design, analysis, and HIL simulation of

embedded control systems which may found at

https://groups.google.com/d/forum/Book_PSK2018

In order to use the .M- and .SLX-files, the readershould haveat his/her disposition

MATLAB and Simulink version R2016a or higher, with Control System Toolbox™

and Robust Control Toolbox™ . The programs described in Chapter 5 require the

availability of Simulink Support Package forArduino hardware andArduino IDE. The

programs presented in Chapters 6 and 7 require the installation of Code Composer

Studio™ release 6.0.0, Control Suite version 3.3.9 and C2000 Code Generation Tools

version 6.4.6.

Sofia, Bulgaria Petko Petkov

December 2017 Tsonyo Slavov

Jordan Kralev

Chapter 1

Embedded control systems

In this chapter, we make a concise overview of embedded control systems and dis-

cuss some aspects of the corresponding hardware and software which is used in these

systems. The embedded control systems are digital systems and their performance is

affected by sampling and quantization errors. That is why, we present some basic

elements of fixed-point and floating-point computations and describe the round-

ing errors associated with these computations. In case of fixed-point arithmetic,

the emphasis is put on the scaling problem, which is the most important issue in

using such arithmetic. We describe briefly the stages of embedded controller design,

controller simulation, and implementation.

1.1 Introduction

According to a popular definition, every electrical or mechanical system that contains

a controller, implemented on the base of digital processor, is called embedded system.

The embedded control systems are systems in which are implemented algorithms for

real-time control using feedback. The embedded control systems represent synthesis

between modern digital technologies and control theory methods. It is necessary

to distinguish between general purpose computational devices (computers) and the

embedded system processors. The computers may execute a great number of programs

with different purpose which are used to solve computational problems. On the other

hand, the embedded system processor, which may be very powerful, performs only a

special control program. Also, the embedded system controller may contain additional

hardware which distinguishes it from the general purpose computer. Most of the

contemporary embedded systems are implemented on the basis of microcontrollers—

computational devices whose functional blocks (central processor, memory, input and

output devices, and interface buses) are combined on a single chip. From hardware

point of view, the microcontrollers represent a very-large-scale integration (VLSI)

circuits.

To work successfully in real time, the embedded system should be developed so

that the required computational cycle fits in the given time interval. For this aim, it is

necessary to choose processor with appropriate computational efficiency, to develop

2 Design of embedded robust control systems using MATLAB

/Simulink

fast control algorithm and to create interface schemes with minimum possible delay

of signal transmission. On the second place, the embedded control system should

possess stability in respect to external data. If, for instance, the data, necessary to

obtain the result, do not arrive in time, then the system cannot produce the required

result in time. In such a case, the system should not lock, but has to continue to give

appropriate result in real time.

The process of developing embedded control systems has strongly multidisci-

plinary character, since it is required to perform a system integration of problems,

associated with

– derivation of mathematical models of physical plants, sensors, communication

hardware, and so on,

– development of methods for high performance control,

– embedding of control algorithms in different hardware and software platforms,

– carrying out communication with remote plants,

– solving problems associated with power supply.

The theoretical foundation of the embedded control systems is the theory of

hybrid systems. The hybrid systems combine continuous processes described by dif-

ferential or difference equations and discrete-event processes, described by finite

automata. Such systems arise in a natural way in the control of continuous processes

by the aid of digital devices and their investigation require a synthesis of control

theory and computer science. The usage of complicated robust and adaptive control

laws leads to the necessity of developing embedded system which work under the

conditions of restricted processor accuracy and relatively small sampling interval.

This represents a serious challenge both from theoretical and practical point of

view.

1.2 Structure and elements of embedded control systems

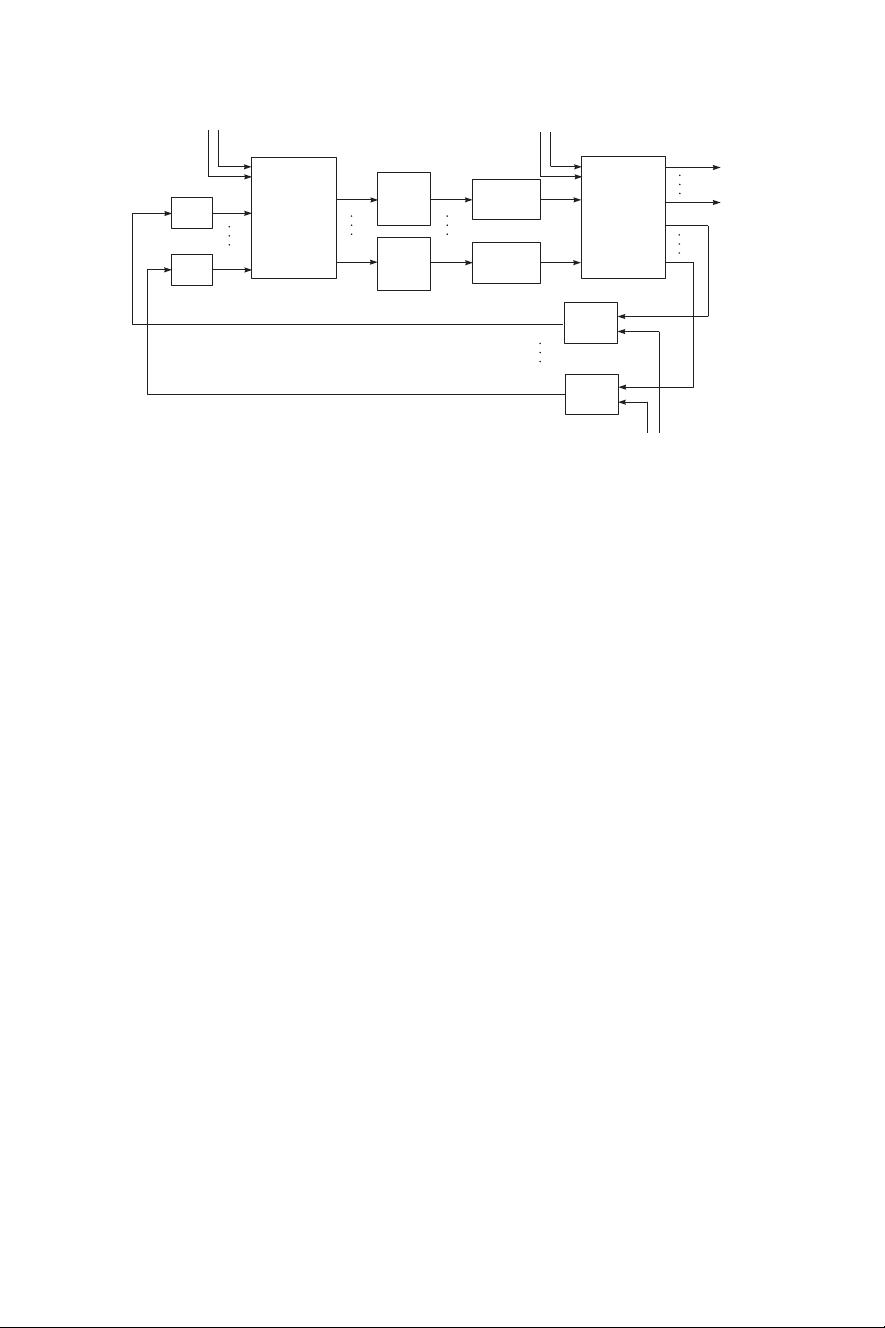
1.2.1 Typical block diagram

From control theory point of view, the embedded control system for a continuous-

time plant represents a closed-loop multivariable digital control system with a block

diagram, shown in Figure 1.1. Very few plants encountered in practice are inherently

digital, so we assume that generally the plant is continuous-time. Such systems are

called sampled-data systems.

The aim of the control system is to ensure desired behavior of controlled plant

outputs in accordance with the reference signals in presence of unknown distur-

bances and noises in the closed loop. In the general case, the plant has m analog

control inputs produced by actuators and r analog outputs measured by the respective

sensors. The measurements are corrupted by noises which, along with the plant distur-

bances, may significantly affect the closed-loop system behavior. The analog sensor

Embedded control systems 3

A/D

(k)

References

Digital

computer

Actuator

Disturbances

Plant

Noises

Sensor

Controlle

outputs

Measured

outputs

Actuator

D/A

with

S/H

D/A

with

S/H

(k)

(t)

(k)

Figure 1.1 Block diagram of an embedded control system

signals are sampled with sampling period T

by an impulse sampler, which produces

digital representations y

(k), y

(k), ..., y

(k) of the measured signals, where y

(k)

means the value of y

(t) for t = kT

, k = 1, 2, .... The sampler is a device, driven

by the system clock, that is converting a continuous-time signal into a sequence of

numbers. Normally, the sampler is combined into analog-to-digital (A/D) converter,

which also quantizes the sequence of numbers into a finite precision number. (Note

that the impulse sampler by itself does not have any physical meaning.) The digital

measurement signals are used by the controller algorithms, embedded in the digi-

tal computer, to produce the digital control signals u

(k), u

(k), … , u

(k). These

signals are converted to the corresponding actuator inputs u

(t), u

(t), ..., u

(t)by

using digital-to-analog (D/A) converters. The purpose of the D/A conver ters is to pro-

duce analog approximations of the digital signals using appropriate reconstruction

algorithms. The analog signals u

(t), u

(t), ..., u

(t) are determined by hold devices

during the sample period until the next sample arrives and the process of holding

each of the samples is termed sample and hold (S/H). The analog signals u

(t) are

used as actuator inputs to control the plant behavior. The work of the A/D and D/A

converters is synchronized by the system clock with the work of the digital computer.

Note that the block diagram may contain additional elements like antialiasing filters

whose function is described in the next section. Also, it is possible that the outputs

of the analog sensors are sampled at different periods and the system may have many

controllers with different sampling periods. In the cases where the sensors have digital

outputs or/and the actuators have digital inputs, the block diagram shown in Figure 1.1

may still be valid taking into account that the A/D and D/A conversion is performed

inside the corresponding devices.

剩余533页未读，继续阅读

THESUMMERE

粉丝: 23
资源: 328

MATLAB/Simulink在嵌入式鲁棒控制系统设计中的应用

利用MATLAB/Simulink设计嵌入式鲁棒控制系统——CART详解

霍乱与城市卫生：19世纪的传染病控制

利用MATLAB/Simulink设计嵌入式鲁棒控制系统

使用Matlab/Simulink设计嵌入式鲁棒控制系统

使用MATLAB/Simulink设计嵌入式鲁棒控制系统

使用Matlab/Simulink设计嵌入式控制系统：响应鼠标键盘事件

现代统计图形系统与MATLAB/Simulink在嵌入式控制中的应用

iOS版微信抢红包Tweak.zip小程序

毕业设计&课设_篮球爱好者网站，含前后台管理功能及多种篮球相关内容展示.zip

基于springboot社区停车信息管理系统.zip

最新资源