Catalan数在算法中的应用分析

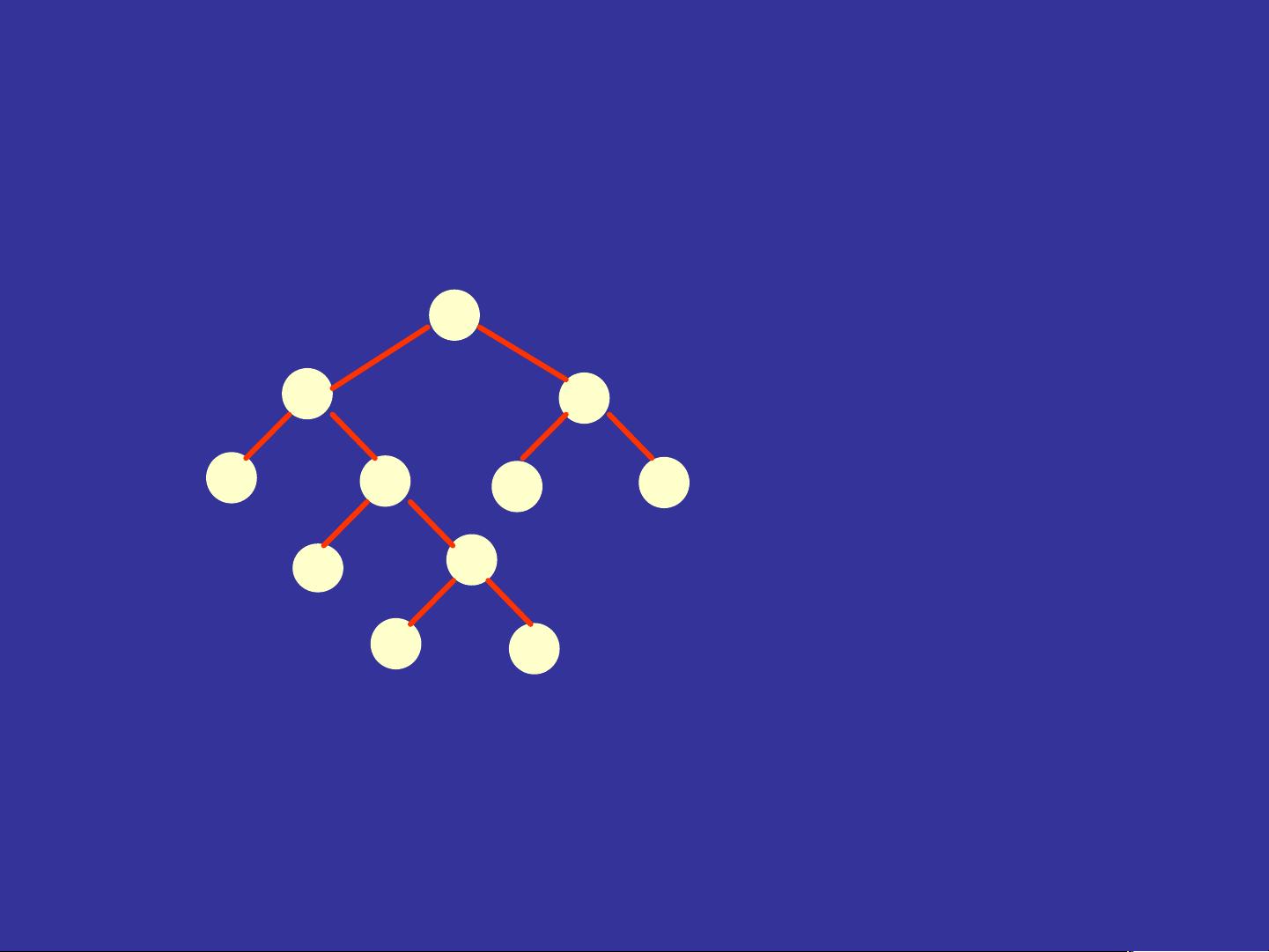
"这篇资源主要讨论了算法中的递推与递归问题，特别是与树的遍历和Catalan数相关的应用。通过分析先序、中序和后序遍历的特点，介绍了如何利用递归来构造和解码二叉树。同时，提到了Catalan数的递推公式和它在解决特定计数问题时的应用，如限制性排列问题和与栈操作序列相关的模式。此外，还提及了二叉树的基本概念和它们的数量统计问题。" 在计算机科学中，递推与递归是解决问题的重要方法，特别是在算法设计中。递推通常通过定义一系列基本项和递推关系来解决数学问题，而递归则是在函数调用自身来解决问题。在这个资源中，递归被用来重建二叉树，基于给定的先序、中序或后序遍历序列。 后序遍历的最后一个元素是树的根节点，而中序遍历中的根节点将左右子树分开。根据这些特性，可以使用递归策略分别处理左子树和右子树，从而实现先序遍历。先序遍历的顺序是根-左-右，因此在构建树的过程中，先输出根节点，然后递归处理左子树，最后处理右子树。 Catalan数是一个在数学和计算机科学中广泛应用的数列，具有特定的递推关系。资源中展示了Catalan数的递推公式和组合公式，并通过实例解释了如何识别和转化问题为Catalan数模型。例如，当解决n个A和n个B的排列问题，限制B的数量不超过A的数量时，可以通过Catalan数来计算可能的排列数量。 栈的问题分析进一步阐述了Catalan数的应用，比如在描述进栈和出栈操作序列时，每个时刻"1"（进栈）的数量总是大于或等于"0"（出栈）的数量。将这个问题转化为二进制数的扫描问题，要求在任何时候"0"的累计数不大于"1"的累计数，也对应了Catalan数的计算。 最后，资源提到了二叉树的基本定义和性质，以及如何计算不同形态的二叉树数目。二叉树是每个节点最多有两个子节点的数据结构，它的遍历方法（前序、中序、后序）是理解和构建二叉树的关键。通过递归，可以枚举所有可能的二叉树形态。 这个资源深入探讨了递推和递归在算法和数据结构中的应用，特别是与树遍历、Catalan数和栈操作序列相关的问题，对于理解这些概念和解决相关问题具有很高的价值。