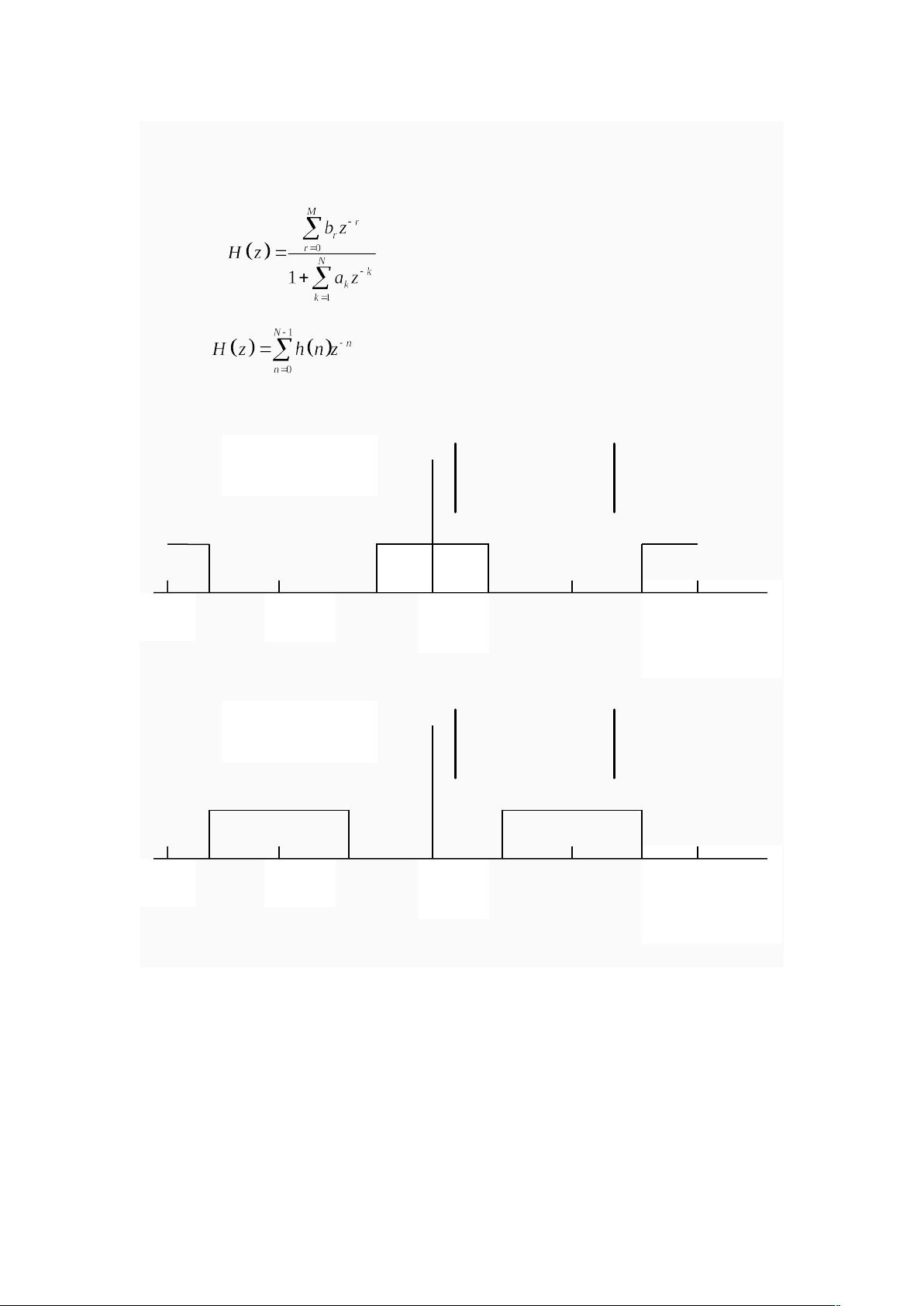
MATLAB实现：双线性变换法设计切贝雪夫低通滤波器

"该资源是一份关于利用双线性变换法设计切贝雪夫低通滤波器的课程设计报告，旨在让学生通过实践掌握MATLAB在数字信号处理中的应用，特别是IIR和FIR滤波器的设计。报告详细介绍了数字滤波器的基本概念、分类及其在不同领域的应用，并聚焦于双线性变换法在实现切贝雪夫低通滤波器中的作用。" 在数字信号处理中，双线性变换法是一种常用的技术，用于将连续时间的滤波器设计转换为离散时间滤波器设计。这种方法在保留了原始滤波器特性的基础上，能够避免频率混叠现象，同时保持了模拟滤波器的性能特征。切贝雪夫滤波器则以其在通带和阻带边缘的陡峭过渡而著名，特别适用于需要严格控制频率响应的场合。 切贝雪夫低通滤波器具有多个等效阶数的实现，每种实现都有不同的频率响应特性。在设计这类滤波器时，通常需要考虑以下关键因素： 1. **频率响应**：滤波器的频率响应定义了其在不同频率下的增益，低通滤波器允许低频信号通过，而衰减高频信号。切贝雪夫滤波器的通带内具有平坦的增益，而在阻带内则快速下降。 2. **阶数**：滤波器的阶数决定了其频率响应的陡峭程度，阶数越高，过渡带越窄，但可能引入更多的相位失真。 3. **截止频率**：低通滤波器的截止频率决定哪些频率会被衰减。低于截止频率的信号通过，高于此频率的信号被逐渐减弱。 4. ** ripple**：在切贝雪夫滤波器的通带和阻带内可能会出现幅度波动，这是其特征之一，通常需要根据具体应用来平衡这个特性。 5. **双线性变换**：这种方法将s域（连续时间）的滤波器转换到z域（离散时间），通过非线性映射保持了频率响应的形状，但改变了频率坐标。 在MATLAB环境中，设计切贝雪夫低通滤波器涉及以下几个步骤： 1. **定义规格**：确定滤波器的通带边界、阻带边界、允许的 ripple 和目标阶数。 2. **计算系数**：使用MATLAB的滤波器设计函数（如`butter`, `cheby1`, `cheby2`等）来计算IIR滤波器的系数。 3. **双线性变换**：使用`bilin`函数将模拟滤波器的系数转换为数字滤波器的系数。 4. **验证性能**：通过仿真或实际数据测试滤波器的性能，检查频率响应、阶跃响应和脉冲响应等特性。 在实际应用中，数字滤波器设计不仅限于理论计算，还需要考虑实际硬件限制和实时处理的效率。双线性变换法提供了一种实用的工具，使得在数字系统中实现复杂的滤波功能成为可能，广泛应用于通信、音频处理、图像处理以及生物医学信号分析等领域。通过这样的课程设计，学生能够深入理解和熟练掌握数字信号处理的关键技术和工具，为未来的工程实践打下坚实基础。