卷积神经网络的数学公式

C#卷积神经网络（Convolutional Neural Network，CNN）是一种常用于图像识别计算机视觉任务的深度学习模型。它通过使用卷积层、池化层和全连接层等组件来提取图像特征并进行分类。

数学公式在描述CNN时起到了重要的作用。下面是CNN中几个关键概念的数学公式：

1. 卷积操作：
在CNN中，卷积操作用于提取图像的局部特征。假设输入图像为X，卷积核为W，那么卷积操作可以表示为：
其中，* 表示卷积操作，Y 是输出特征图。

2. 激活函数：
在卷积层或全连接层后，通常会应用一个非线性激活函数来引入非线性变换。常见的激活函数有ReLU、Sigmoid和Tanh等。以ReLU函数为例，其数学公式为：

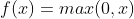
3. 池化操作：
池化操作用于降低特征图的空间维度，并保留重要的特征。常见的池化操作有最大池化和平均池化。以最大池化为例，其数学公式为：

4. Softmax函数：
在CNN中用于多分类问题时，通常会使用Softmax函数将网络输出转换为概率分布。Softmax函数可以表示为：
其中，S_i 是第 i 个类别的概率，X_i 是网络输出的第 i 个元素。

这些是CNN中一些常见的数学公式，它们在实现卷积神经网络时起到了关键作用。