MATLAB拟合与图像处理：探索应用，提升图像质量

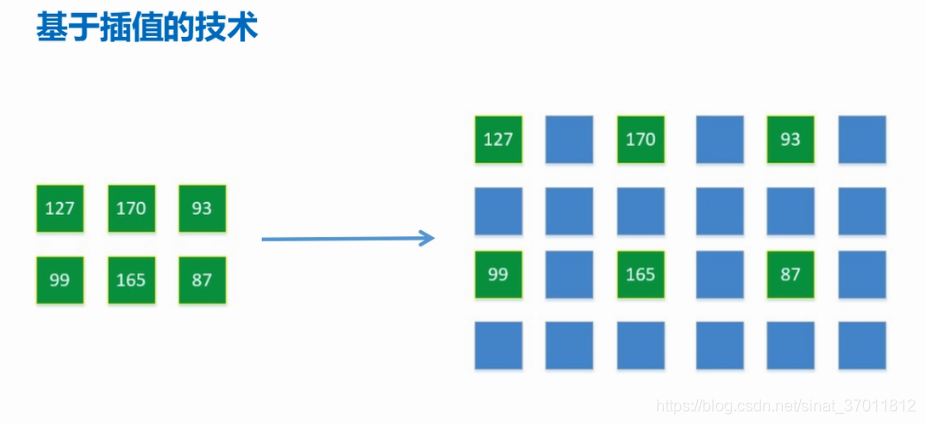
# 1. MATLAB拟合与图像处理概述**

MATLAB是一个强大的技术计算平台，广泛应用于科学、工程和数据分析领域。它提供了丰富的函数库，用于拟合和图像处理。

拟合是指根据给定数据点找到最佳的数学函数或模型。MATLAB提供了各种拟合方法，包括线性回归、多项式拟合和曲线拟合。这些方法可用于预测数据、发现趋势和优化系统。

图像处理涉及对数字图像进行操作，以增强、分析和理解它们。MATLAB提供了图像处理工具，用于图像增强、分割、特征提取和分析。这些工具可用于图像质量提升、对象检测和图像识别。

# 2. MATLAB拟合理论与实践**

**2.1 线性回归拟合**

**2.1.1 最小二乘法原理**

线性回归拟合是一种常见的拟合方法，其目标是找到一条直线，使得它与给定数据点的平方误差最小。最小二乘法原理是线性回归拟合的基础，其原理是通过最小化残差平方和来确定直线方程。残差平方和定义为：

SSE = Σ(y_i - y_hat_i)^2

其中：

* SSE：残差平方和
* y_i：第i个数据点的实际值
* y_hat_i：第i个数据点的拟合值

**2.1.2 拟合方程求解**

最小二乘法原理的数学推导可以得到线性回归的拟合方程：

y = mx + b

其中：

* y：因变量
* x：自变量
* m：斜率
* b：截距

斜率和截距可以通过以下公式计算：

m = (Σ(x_i - x̄)(y_i - ȳ)) / Σ(x_i - x̄)^2
b = ȳ - m * x̄

其中：

* x̄：自变量的均值
* ȳ：因变量的均值

**2.2 多项式拟合**

**2.2.1 多项式回归模型**

多项式拟合是线性回归的一种扩展，它使用多项式方程来拟合数据。多项式回归模型的一般形式为：

y = β_0 + β_1 * x + β_2 * x^2 + ... + β_n * x^n

其中：

* β_i：多项式系数
* n：多项式的阶数

**2.2.2 拟合系数计算**

多项式回归系数可以通过最小二乘法原理计算。对于n阶多项式，需要求解n+1个系数。系数的计算公式为：

[X^T * X] * β = [X^T * y]

其中：

* X：设计矩阵，包含自变量的幂次
* y：因变量向量
* β：系数向量

**2.3 曲线拟合**

**2.3.1 非线性拟合方法**

曲线拟合用于拟合非线性数据。常见的非线性拟合方法包括：

* 指数拟合
* 对数拟合
* 幂律拟合
* 高斯拟合

**2.3.2 拟合参数优化**

非线性拟合需要优化拟合参数，以最小化拟合误差。常用的优化方法包括：

* 最小二乘法
* 最大似然估计
* 贝叶斯推断

**代码示例：**

% 数据准备
x = [1, 2, 3, 4, 5];
y = [2, 4, 5, 4, 5];

% 线性回归拟合
p = polyfit(x, y, 1);
y_fit = polyval(p, x);

% 绘制拟合曲线
figure;
plot(x, y, 'o');
hold on;
plot(x, y_fit, '-r');
legend('数据点', '拟合曲线');

% 多项式拟合
p = polyfit(x, y, 2);
y_fit = polyval(p, x);

% 绘制拟合曲线
figure;
plot(x, y, 'o');
hold on;
plot(x, y_fit, '-r');
legend('数据点', '拟合曲线');

# 3.1 图像增强

#### 3.1.1 灰度变换

灰度变换是图像处理中最基本的增强技术之一，它通过调整图像中像素的灰度值来改善图像的对比度、亮度和对比度。灰度变换有许多不同的类型，每种类型都有其独特的特点和应用。

**线性灰度变换**

线性灰度变换是一种最简单的灰度变换，它通过以下公式将输入图像中的每个像素值映射到输出图像中：

output_pixel_value = a * input_pixel_value + b

其中，`a`和`b`是控制变换的两个参数。`a`控制输出图像的对比度，`b`控制输出图像的亮度。

**非线性灰度变换**

非线性灰度变换是一种更复杂的灰度变换，它使用非线性函数将输入图像中的每个像素值映射到输出图像中。非线性灰度变换可以产生更复杂的图像增强效果，例如伽马校正和直方图均衡化。

**伽马校正**

伽马校正是一种非线性灰度变换，它通过以下公式将输入图像中的每个像素值映射到输出图像中：

output_pixel_value = input_pixel_value^gamma

其中，`gamma`是一个控制变换的参数。`gamma`大于1时，图像变亮；`gamma`小于1时，图像变暗。

**直方图均衡化**

直方图均衡化是一种非线性灰度变换，它通过将输入图像的直方图拉伸到整个灰度范围来改善图像的对比度